[ emiraga @ 10.02.2006. 12:31 ] @
| Eulerova formula http://en.wikipedia.org/wiki/Euler's_formula iz koje se lahko nalazi Eulerov identitet http://en.wikipedia.org/wiki/Euler's_identity 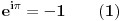 Nista nam ne brani da stepenujemo na -1 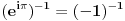 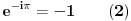 Sabiranjem formula (1) i (2) i kracenjem -1 dobijamo 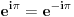 Uradimo ln obje strane 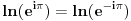 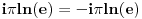 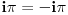 Nakon dijeljenja dolazimo do 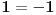 Na ovako nesto nisam naisao prije, kao sto je profesor sa Harvarda rekao: "It is absolutely paradoxical; we cannot understand it, and we don't know what it means, but we have proved it, and therefore we know it must be the truth." Volio bih da mi neko pokaze gdje bi mogla biti greksa. Za one koji misle da je greska sto smo mozda uzeli logaritam od negativnog broja neka jos jednom razmisle. Ako vam je dodijalo razmisljati: http://mathforum.org/library/drmath/view/55564.html http://www.newton.dep.anl.gov/askasci/math99/math99180.htm [Ovu poruku je menjao Bojan Basic dana 10.02.2006. u 14:01 GMT+1] [Ovu poruku je menjao emiraga dana 10.02.2006. u 14:30 GMT+1] |