Citat:
Valerij Zajcev:
sta ja sad radim pretvorim u razlomke...
5/10; 25/100; 125/1000; 625/10000;
To je zgodan trenutak da svaki od tih razlomaka dovedeš u tzv. sveden oblik, tj. da brojilac i imenilac budu uzajamno prosti (dakle, da nemaju zajedničkih delilaca - osim broja
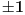
).
Tako da je jedna mogućnost:
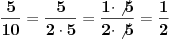
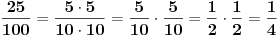
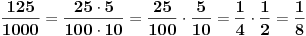
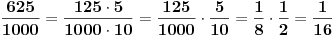
Citat:
Valerij Zajcev:
zbog negativnih stepena pisem:
1/5/10; spoljasnji sa spoljasnjim unutrasnji sa unutrasnjim;
Ako imaš situaciju
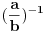
to je zaista kao što si napisao
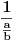
, odnosno
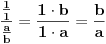
- dakle to je ono pravilo koje si pomenuo "spoljašnji sa spoljašnjim...". Tako da smo faktički iz toga izveli novo pravilo:
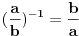
ili opštije
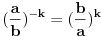
.
nastavak preskočiti u prvom čitanju
Drugim rečima ako imaš neko
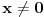
, onda je
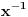 oznaka
oznaka za broj koji pomnožen sa

daje rezultat

. Može se lako pokazati da za dato
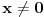
postoji tačno jedan broj sa takvim svojstvom. Taj broj
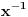
zovemo inverzom od

.
Pošto važi
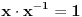
vidimo da je i
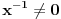
, pa sledi da je inverz broja
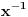
u stvari broj

. Tu činjenicu možemo da zapišemo kao
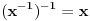
(Inverzan broj broja
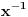
je broj

) Znači, brojevi

i
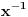
su jedan drugome inverzni (kaže se i: uzajamno inverzni).
Specijalno, za
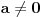
i
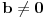
važi
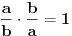
što, između ostalog, znači i da je
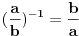
ili ako više voliš
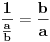
.
[Ovu poruku je menjao uranium dana 11.02.2006. u 23:11 GMT+1]