[ buha18 @ 12.02.2006. 11:01 ] @
| znaci, treba dokazati da je lim(x ide u beskonacno) [sin(x)]/(x) ==1 ima li netko to izvedeno?ž pozdrav |
|
[ buha18 @ 12.02.2006. 11:01 ] @
[ cob4lt @ 12.02.2006. 11:24 ] @
Jesi li se ti mozda zabunio pa da nije da [sin(x)]/x tezi 0?
Inace ja bi to ovako napisao Lim [Sin(x)] * 1/x, a posto znas da je 1/x = 0 onda je i ovo jednako 0 pa to znaci da to tezi prema 0 [ buha18 @ 12.02.2006. 13:43 ] @
1/0 je 0?
ja sam mislio prvo da je beskonacno :-) nisam se zabunio. tezi ka 1. :-) [ Bojan Basic @ 12.02.2006. 13:48 ] @
[ buha18 @ 12.02.2006. 17:23 ] @
ovo gornje
kad limes tezi u jedan... [ braker @ 12.02.2006. 18:19 ] @
Nacrtaj jedinichnu kruznicu.Postavi pochetak koordinatnog sistema u centar.Povuci polupravu iz tachke O(centar kruga)pod nekim uglom u odnosu na osu x.Mesto preseka poluprave i kruznice oznachi sa M.Iz tachke M spusti normalu na x osu.Ovu tachku oznachi sa N.Mesto preseka kruznice i ose x oznachi sa 1.Iz tachke 1 povuci normalu:mesto preseka sa polupravom oznachi sa P.Duz ON=cosx,MN=sinx i 1P=tgx.
Sa slike se vidi da je trougao ONM deo sektora O1M,a ovaj je deo trougla O1P.Iz odnosa povrshina likova dobijamo: 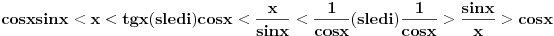 Odavde zbog 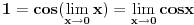 sledi egzistencija limesa od sledi egzistencija limesa od 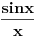 kada x tezi 0 i valjanost kada x tezi 0 i valjanost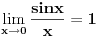 P.S.Mrzi me trazim kako se pishe ovo sledi u (la)tex-u.sorry edit:Valjda:limes... je jednak jedan kada x tezi 0. [Ovu poruku je menjao braker dana 12.02.2006. u 19:24 GMT+1] [ petarm @ 20.03.2006. 12:54 ] @
Ovo je dokaz koji je i meni poznat! Voleo bih da ako neko zna jos neki nacin da se ovo dokaze to i napise. To mozes reci i ovako sinx~x, kad x tezi ka nuli. Sto bi znacilo sinx se ponasa kao x kad x tezi nuli. Ali kolko sam ja tebe razumeo tebi nije trebao pravi dokaz vec nesto sto ce da te uveri da je to tako. Nacrtaj pravu y=x i sinusoidu i sa slike vidi sta se desava blizu nule!
[ Lobacev @ 23.03.2006. 13:31 ] @
Ima i Lopitalovo pravilo (L'Hospital, ako se ne varam), po kome je limes sin(x)/x kada x->0 jednak odnosu prvih izvoda ovih funkcija, t.j. jednak je cos(x)/1 za x=0 a to je 1. Ili da se sin(x) razvije u red pa da se svaki član tog reda podeli sa x.
[ srki @ 23.03.2006. 13:46 ] @
Ne mozes to da koristis u dokazu jer se cinjenica da je sinx/x=1 kada x tezi nuli koristi da bi se dokazalo da je izvod od sin(x) jednak kosinusu. Ispalo bi da ti posredno koristis sin(x)/x=1 da bi dokazao to isto.
[ uranium @ 23.03.2006. 14:54 ] @
To je tačno, ako se trigonometrijske f-je definišu geometrijski, međutim ima i primera analitičkih "čistunaca" koji osnovne trig. f-je definišu ovako:
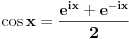 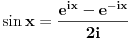 tako da se u dokazu činjenice 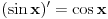 ne koristi ne koristi 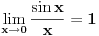 . .Mada sumnjam da je Lobacev imao u vidu baš tu definiciju [Ovu poruku je menjao uranium dana 23.03.2006. u 16:29 GMT+1] [ Lobacev @ 23.03.2006. 16:39 ] @
A kako bi našli limes sqrt(x*x-1)/x kada x-> beskonačnosti isključivo Lopitalovim pravilom?
[ Lobacev @ 24.03.2006. 11:00 ] @
Takođe pogledaj http://www.ms.uky.edu/~carl/ma330/sin/sin1.html
[ Nedeljko @ 04.04.2006. 23:03 ] @
Dokazi osnovnih stavova zavise od definicija koje se koriste, i samo tada njihovo dokazivanje ima smisla.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|