[ anon75319 @ 18.02.2006. 21:43 ] @
| Treba mi dobra knjiga koja objašnjava linearnu algebru. Na razini 1. razreda srednje škole... Ako tako nešto postoji molio bih da mi date link ili nesto drugo. |
|
[ anon75319 @ 18.02.2006. 21:43 ] @
[ Alexsis @ 29.03.2008. 22:59 ] @
http://lavica.fesb.hr/~slap/
msever.fizika.org/predavanja/LA2%20-%20skripta.pdf Jel zna neko za neku kvalitetnu zbirku sa resenim zadacima i objasnjenjima iz ove oblasti? [ Miladinovic @ 02.11.2008. 20:05 ] @
Pozdrav,
Da ne bih otvarao novu temu, jer verujem da je pitanje prosto, naime interesuje me šta su sopstveni vekotri matrice, oderedio sam karakeristični polinom neke zadate matrice i iz tog polinoma se vide sopstvene vrednosti iste, e sada me zanima kako odrediti sopsvene vektore? [ peddja_stankovic @ 02.11.2008. 21:41 ] @
zameni jednu sopstvenu vrednost u sistem (A-lamda*I)*(x,y,z)^T=(0,0,0)^T tako sto prakticno koeficijentima na glavnoj dijagonali oduzmes tu sopstvenu vrednost i kazes =0. takav sistem mora da ima beskonacno mnogo resenja sa jednim ili vise parametara alfa, beta ... Ako ima na primer parametarsko resenje (alfa,2*alfa,3*alfa) uzmi alfa=bilo_koji_broj_sem_0=naprimer 1.
onda je sopstveni vektor (1,2,3). Ako dobijes beskonacno omnogo resenja sa 2 slova alfa i beta dobices i dva sopstvena vektora tako sto jedan vektor dobijas za na primer alfa=1 i beta=0 a drugi sopstveni vektor za alfa=0 a beta=1. moras tako zameniti sve sopstvene vrednosti i na opisan nacin podobijati sve sopstvene vektore [ Miladinovic @ 03.11.2008. 15:21 ] @
Zahvaljujem na iscrpnom odgovoru!
[ devetkamp @ 15.12.2012. 12:06 ] @
Jel moze pomoc oko dokaza teoreme...
[ Sonec @ 15.12.2012. 13:25 ] @
Da preformulisem pitanje:
Neka su 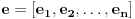 i i 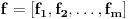 dva sistema vektora vektorskog prostora dva sistema vektora vektorskog prostora  . Ako je . Ako je 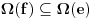 i i  linearno nezavisan, onda je linearno nezavisan, onda je 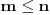 . (gde je sa . (gde je sa 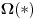 obelezen skup svih linearnih kombinacija vektora iz obelezen skup svih linearnih kombinacija vektora iz  (iliti, linearni omotac skupa (iliti, linearni omotac skupa  ) )Dokaz: Indukcijom po  . Neka je . Neka je  , tada je , tada je 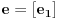 i i 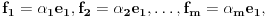 . Pretpostvimo da je . Pretpostvimo da je 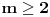 i posmatrajmo sistem i posmatrajmo sistem 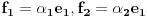 . Tada je . Tada je 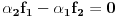 i znamo da je i znamo da je  linearno nezavisan sistem, pa je linearno nezavisan sistem, pa je 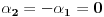 , pa je , pa je 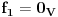 i i 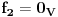 , sto je kontradikcija jer u linearno nezavisnom sistemu ne moze da bude nula vektora. , sto je kontradikcija jer u linearno nezavisnom sistemu ne moze da bude nula vektora.Pretpostavimo da je tvrdjenje tacno za sve pocetne sisteme  sa manje od sa manje od  vektora i neka je vektora i neka je 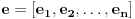 . Tada znamo da vazi: . Tada znamo da vazi: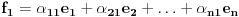 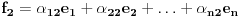 ..... 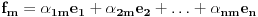 , ,odnosno 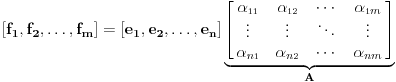 Dakle, 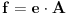 . .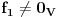 to sledi da za neko to sledi da za neko  vazi vazi 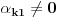 Posmatrajmo sistem: 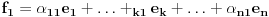 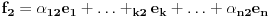 ..... 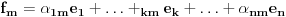 Pomnozimo prvu jednacinu sa 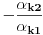 i dodajmo drugoj, ponovimo postupak za preostale jednacine (u poslednjem koraku cemo pomnoziti prvu jednacinu sa i dodajmo drugoj, ponovimo postupak za preostale jednacine (u poslednjem koraku cemo pomnoziti prvu jednacinu sa 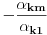 i dodati je poslednjoj jednacini) i dodati je poslednjoj jednacini)Dobijamo nov sistem: 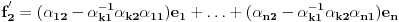 ... 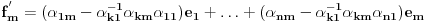 Primetimo da se nigde ne pojavljuje 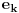 . .Kako je 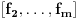 linearno nezavisan, to je i sistem linearno nezavisan, to je i sistem 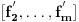 linearno nezavisan. linearno nezavisan.Takodje, 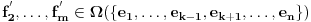 , pa je i , pa je i 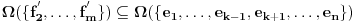 , te mozemo primeniti induktivnu hipotezi, pa vazi , te mozemo primeniti induktivnu hipotezi, pa vazi 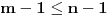 , odnosno , odnosno 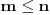 [ Nedeljko @ 15.12.2012. 14:22 ] @
Postoji lema o zameni iz koje ovo sledi i to ne samo u konačnom slučaju.
Pretpostavimo da su sistemi oblika 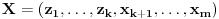 i i 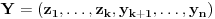 , pri čemu može biti i , pri čemu može biti i 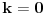 . Ako je . Ako je 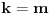 , onda tvrđenje neposredno sledi jer je , onda tvrđenje neposredno sledi jer je 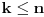 . Pretpostavimo zato da je . Pretpostavimo zato da je 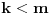 . .(1) 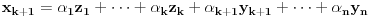 . .Obzirom da je sistem  linearno nezavisan, vektor linearno nezavisan, vektor 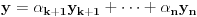 je različit od nule. Stoga postoji neko je različit od nule. Stoga postoji neko 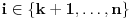 takvo da je takvo da je 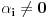 . Razmotrimo sistem . Razmotrimo sistem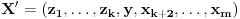 . .Na osnovu izbora vektora  svaki element sistema svaki element sistema 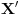 pripada linearnom omotaču sistema pripada linearnom omotaču sistema  . .Takođe, sistem 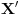 je linearno nezavisan. U protivnom važi je linearno nezavisan. U protivnom važi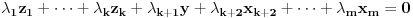 , ,pri čemu bar jedan od skalara  nije nula. Zbog linearne nezavisnosti sistema nije nula. Zbog linearne nezavisnosti sistema  mora biti mora biti 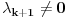 , pa je , pa je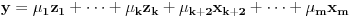 , ,za neke skalare 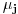 . Međutim, na osnovu (1) je . Međutim, na osnovu (1) je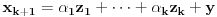 , ,odnosno vektor 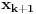 je linearna kombinacija preostalih vektora sistema je linearna kombinacija preostalih vektora sistema  , što ej u suprotnosti sa njegovom linearnom nezavisnošću. , što ej u suprotnosti sa njegovom linearnom nezavisnošću.Neka je 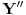 sistem koji se dobija od sistema sistem koji se dobija od sistema  zamenom vektora na mestu zamenom vektora na mestu  sa sa  . On ima isti lineani omotač kao . On ima isti lineani omotač kao  . Zaista, vektor . Zaista, vektor  je linearna kombinacija vektora sistema je linearna kombinacija vektora sistema  , a vektor , a vektor 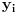 je linearna kombinacija vektora sistema je linearna kombinacija vektora sistema 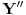 na osnovu izbora vektora na osnovu izbora vektora  i i 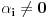 . .Neka je 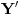 sistem koji se dobija zamenom vektora na mestima sistem koji se dobija zamenom vektora na mestima 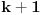 i i  u sistemu u sistemu 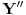 . On ima isti linearni omotač kao i sistem . On ima isti linearni omotač kao i sistem 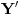 pa samim tim i pa samim tim i  . .Međutim, sistemi 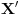 i i 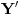 imaju prvih imaju prvih 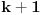 elemanata zajedničkih. Produžavajući ovaj postupak dolazimo do slučaja elemanata zajedničkih. Produžavajući ovaj postupak dolazimo do slučaja 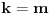 , koji je rešen. , koji je rešen.[ darkosos @ 15.12.2012. 23:51 ] @
Nisam siguran, ali zar nije
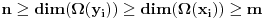 ? Prva nejednakost je posledica toga da je generator set (valjda se tako zove, zaboravio sam) uvek ima elemanata bar koliko i baza VP. Druga je posledica toga sto se svaki ? Prva nejednakost je posledica toga da je generator set (valjda se tako zove, zaboravio sam) uvek ima elemanata bar koliko i baza VP. Druga je posledica toga sto se svaki  moze izraziti preko linearne kombinacije moze izraziti preko linearne kombinacije 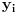 pa znaci da pa znaci da 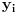 generise VP koji je nadprostor od onog koji generise generise VP koji je nadprostor od onog koji generise  . I na kraju, posto je . I na kraju, posto je  skup linearno nezavisnih vektora, on je manji ili jednak bazi prostora skup linearno nezavisnih vektora, on je manji ili jednak bazi prostora 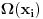 . .[ Nedeljko @ 16.12.2012. 01:41 ] @
Sve je to tačno, ali se pozivaš na pojam dimenzije koji se uvodi kao broj elemenata baze, a na osnovu teoreme da sve baze imaju isti broj elemenata. Ovde se radi o dokazu tvrđenja na osnovu koga se dokazuje da sve baze imaju isti broj elemenata.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|