Ako ti je poznat poluprecnik onda samo uzmes u otvor sestara taj poluprecnik i ocrtas ga sa dvije razlicite tacke na kruznici i u njihovom presjeku je centar.

Zadana je samo kružnica i alat(šestar)!

Pre svega, Maskeronijeva konstrukcija nam garantuje da ako se nešto može konstruisati sa lenjirom i šestarom, može i samo sa šestarom.

Ovo što sledi može da se uradi sa lenjirom i šestarom:

Uzmemo dve različite tačke i sa kružne linije, nađemo središte duži , to je neka tačka , konstruišemo normalu na kroz tačku , dobijemo dve presečne tačke sa krugom i , nađemo središte duži 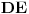i to je centar kruga.

Sad ostaje pitanje kako se ovo prevodi na "šestarski jezik"
Na onom linku je opisano kako se nalazi središte duži, za normalu nam je dovoljan šestar, još samo da neko smisli kako da nađemo preseke normale i kružne linije.

Hm, nisam siguran, u trenutku mi je palo na pamet.

Odredis dve proizvoljne tacke na kruznici - A i B. Iz obe tacke nacrtas kruznice istih poluprecnika koji je veci od AB/2 tako da kruznice imaju dve zajednicke tacke (u kojima se seku). Prava odredjena tim tackama prolazi kroz centar. Ponoviti postupak na tackama preseka dobijene prave i kruznice. Dve dobijene prave se seku u centru.

Hm, nisam siguran, u trenutku mi se dogodio Deja Vu

Evo, ko je odlučio da odustane neka pogleda ovde.
_{U pitanju su 2 fantastična appleta.}

Šestarom ne možeš povući te prave (treba ti i lenjir), tako da ta konstrukcija "ne igra" iako je ispravna.

Pošto imamo samo šestar, jedini način da nađemo bilo kakvu tačku (pa i centar date kružnice) jeste da je konstruišemo kao presek izvesnih kružnica.

Inače, istorijski kuriozitet: ovaj problem svojevremeno je rešio Napoleon Bonaparta i time prilično zadivio svoje učitelje.

Ma, bruka...

Odlican aplet.

Ne znam da li cu lupiti ali cini mi se da se taj problem zove Napoleonov. Toliko znam o tome :)
Pozz