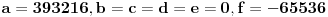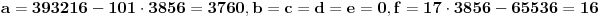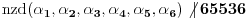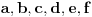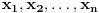[ Lobacev @ 28.02.2006. 09:58 ] @
| Dati su brojevi 17, 23, 29, 37, 43, 101. Treba naći cele pozitivne brojeve (mogu biti i nula) a,b,c,d,e,f tako da broj I = a*17 + b*23 + c*29 + d*37 + e*43 + f*101 bude "najbliži" (ako može i jednak) broju 65536, t.j. da je abs(I-2**16) minimalno. |