Svaki od ona tri integrala koje si naveo su rešivi metodama racionalne integracije za svako konkretno i .



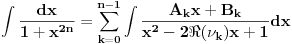
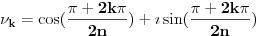
gde je (tj. -ti koren iz )
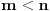
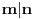
U opštem slučaju ne vidim neku vezu između -tog korena iz i -tih korena iz za (osim u nekim slučajevima kad ) tako da mi se čini da nema neke rekurzije.


Ista priča i za drugi integral, s tim da posmatramo -te korene iz .
Treći slično prvom.

I na kraju, što se tiče integrala binomnog diferencijala i rezultata do kojih je došao Chebyshev - originalni dokaz ima 22 strane a i već na početku se poziva na neke meni nepoznate rezultate Abel-a i Liouville-a pa sam lepo odustao
Doduše ima i indikacija da se neki od rezultata mogu dobiti značajno jednostavnije...

<sub>Je l' možeš da nam otkriješ zašto ispred trećeg integrala piše: "and"?

[Ovu poruku je menjao uranium dana 03.03.2006. u 11:35 GMT+1]</sub>

Da, ma meni je jasno da se to tako radi, ali meni ne polazi za rukom da resim ove sisteme po ... No, izmacovacu se ja nekako... :-)

A jel znas gde ja mogu da skinem taj dokaz (za Chebyshev)?

P.S. "and" pise jer sam slicnu poruku postavio i na jednom engleskom forumu :-)

Pogledaj moju poruku u top temi online resursi... pa na datom linku potraži Izbrannye trudy Chebyshev P.L.

Evo upravo skinuh knjigu. Ali koliko ja vidim ovde nije dat dokaz vec samo teorema i kratak opis postupka?

... kasnije: Ok, moja greska! Nasao sam..

Hvala!

_{[Ovu poruku je menjao cassey dana 04.03.2006. u 01:08 GMT+1]}