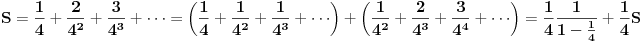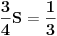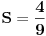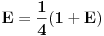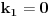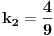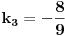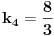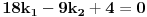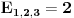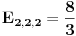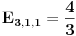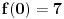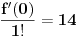[ Bojan Basic @ 09.03.2006. 00:32 ] @
|
[ Farenhajt @ 09.03.2006. 02:37 ] @
Hm, možda mi je rezon pogrešan, ali očekivani dobitak/gubitak svakog igrača u svakom bacanju je nula (0,5 da će izgubiti jedan novčić; 0,25 da će dobiti dva novčića; 0,25 da će ostati na istom). Ne znači li to da je očekivani broj bacanja za bilo koji konačan gubitak beskonačan?
[ Bojan Basic @ 09.03.2006. 12:03 ] @
Izgleda da nisi u pravu. Pretpostavimo da svi imaju samo po jedan novčić. Tada je očekivani broj bacanja do ispadanja jednog od njih zapravo očekivani broj bacanja do prvog odlučenog, a to svakako nije beskonačno.
[ peddja_stankovic @ 09.03.2006. 20:31 ] @
Ja mislim da sam resio trivijalan slucaj kad je l=m=n=1.
Meni ocekivanje ispade 4/3. Sledi obrazlozenje .... [ peddja_stankovic @ 09.03.2006. 22:10 ] @
Obelezimo osobe sa A,B i C i G - grb, P - pismo U prvom bacanju su moguci sledeci ishodi: A B C ----- G G G G G P G P G G P P P G G P G P P P G P P P Ako je GGG ili PPP igra se nastavlja jer niko ne gubi nista i svi i dalje imaju po dinar a sve ostalo dovodi da cak dve osobe ostanu bez para i tu se igra prekida. P("GGG ili PPP")=2/8=1/4 a P("ostalih ishoda")=3/4 Neka je X slucajna promenljiva koja predstavlja broj bacanja do prekida igre. Dakle P(X=1) = P("da nije GGG ni PPP") = 3/4. Dalje, P(X=2) = P("u prvom bacanju je bilo GGG ili PPP a u drugom bacanju jedan od ishoda koji dovode do prekida igre, tj nije bilo ni GGG ni PPP") = 1/4*3/4 Itd, itd. P(X=n) = 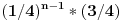 Jasno je da postoji mogucnost da se igra nikad ne zavrsi (ako svaki put padne GGG ili PPP). Slucajna promenljiva X ima takozvanu geomertijsku raspodelu.  Zaboravio sam kako ide matematocko ocekivanje za tu raspodelu, izvescemo je po definiciji za mat. ocekivanje. 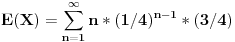 Kad se malo sredi, dobije se 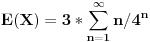 Ne znam bas kako se tacko sumira ovaj red ali MCAD mi izbacio 4/9. Sve u svemu E(X)=3*4/9=4/3 [Ovu poruku je menjao peddja_stankovic dana 09.03.2006. u 23:14 GMT+1] [ Bojan Basic @ 09.03.2006. 22:42 ] @
[ srki @ 10.03.2006. 07:02 ] @
[ Bojan Basic @ 10.03.2006. 11:59 ] @
U pravu si, greška u kucanju.
[ peddja_stankovic @ 12.03.2006. 05:50 ] @
Ja dobih za l=m=n=2 da je E=8/3.
Da li to znaci da je za l=m=n=N, E=N*4/3? [ Bojan Basic @ 12.03.2006. 11:51 ] @
Citat: peddja_stankovic: Ja dobih za l=m=n=2 da je E=8/3. Dobro je. Citat: peddja_stankovic: Da li to znaci da je za l=m=n=N, E=N*4/3? Ne znači, samo se slučajno potrefilo da se za prve dve mogućnosti uklapa u tu formulu. [ peddja_stankovic @ 15.03.2006. 21:49 ] @
Evo novih informacija.
Napravio sam sitan programcic koji simulira bacanje novcica i dobio sam sledece eksperimentalne rezultate: neka je l=m=n=N Vec sam dobio za N=1 E=4/3 N=2 E=8/3 Evo nekih drugih pribliznih vrednosti: N=3 E=5.13 N=4 E=8.52 N=5 E=12.7 N=6 E=18.1 N=7 E=24.1 N=8 E=30.5 N=9 E=38.7 N=10 E=47.67 N=11 E=57.12 .... itd. Sad ce mi biti lakse da dodjem do analiticke formule. Mislim da ce mi trebati manje od 25 godina [ Bojan Basic @ 15.03.2006. 22:12 ] @
[ zzzz @ 17.03.2006. 00:13 ] @
Trebalo bi možda najprije riješiti ovakav zadatak:
Dva kockara imaju po N novčića.U jednom bacanju može se jedan novčić dobiti ili izgubiti.Naći broj bacanja S za koji postoji veća vjerovatnost da jedan od njih ode kući praznih džepova,nego da ne ode. ---------- Za S=N vjerovatnost je mala,pa onda sa porastom S vjerovatnost takođe raste. [ srki @ 19.03.2006. 17:06 ] @
Posmatrajmo jednakostranicni trougao koji ima visinu
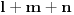 . Oznacimo stranice sa . Oznacimo stranice sa  , ,  i i 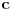 . Neka nam je pocetna tacka . Neka nam je pocetna tacka  udaljena od stranice udaljena od stranice  za duzinu za duzinu  , od stranice , od stranice  za duzinu za duzinu  , od stranice , od stranice 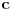 za duzinu za duzinu  . Lako je dokazati da takva tacka postoji i da je jedinstvena. Pretpostavljam da vam je jasno da ce nam pri pomeranju tacke P zbir rastojanja uvek biti . Lako je dokazati da takva tacka postoji i da je jedinstvena. Pretpostavljam da vam je jasno da ce nam pri pomeranju tacke P zbir rastojanja uvek biti 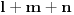 . Pro svakom potezu tacku P pomeramo za vrednost 2 u pravcu jedne visine u smeru suprotnom od stranice koja odgovara toj visini. Tada ce se rastojanja od tacke P od ostalih stranica smanjiti za po 1. Znaci ovaj random walk tacke P u potpunosti odgovara igri koju igraju 2 kockara. Sada verovatno postoji nekakva formula za resavanje tog random walk-a ali ja je ne znam, mogao bih kasnije da pokusam da smislim nesto ali mislim da je moguce naci resenje i bez toga. Posto tacka P radi random walk to znaci da je . Pro svakom potezu tacku P pomeramo za vrednost 2 u pravcu jedne visine u smeru suprotnom od stranice koja odgovara toj visini. Tada ce se rastojanja od tacke P od ostalih stranica smanjiti za po 1. Znaci ovaj random walk tacke P u potpunosti odgovara igri koju igraju 2 kockara. Sada verovatno postoji nekakva formula za resavanje tog random walk-a ali ja je ne znam, mogao bih kasnije da pokusam da smislim nesto ali mislim da je moguce naci resenje i bez toga. Posto tacka P radi random walk to znaci da je 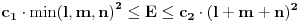 . To nam govori da nasa formula za E sadrzi kvadrate . To nam govori da nasa formula za E sadrzi kvadrate  , ,  i i  . .//edit: ispostavilo se da to nije tacno ali posto navedena nejednakost i dalje vazi onda znamo da je formula priblizno jenaka 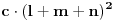 kada su l m i n veliki (i jednaki). kada su l m i n veliki (i jednaki).Imamo 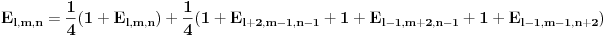 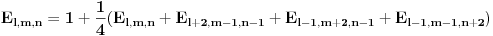 Pretpostavimo da je: 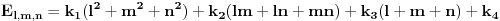 Ubacivanjem u gornju formulu, moguce je naci koeficijente  , ,  , , 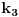 i i 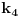 . Ili ako ne moze tako onda jednostavno postavimo jednacine kada je l=m=n=1 gde smo izracunali verpvatnocu 4/3 i to uradimo za jos 3 razlicite vrednosti. . Ili ako ne moze tako onda jednostavno postavimo jednacine kada je l=m=n=1 gde smo izracunali verpvatnocu 4/3 i to uradimo za jos 3 razlicite vrednosti.[Ovu poruku je menjao srki dana 20.03.2006. u 10:54 GMT+1] [ uranium @ 19.03.2006. 22:00 ] @
[ peddja_stankovic @ 20.03.2006. 00:10 ] @
Uranijum, tvoja kalkulacija je tacna ali nesto drugo nije u redu sa formulom.
Mora da se dobije za l=3, m=2, n=1 E=2 a ne 20/9 kako se dobija na osnovu srkijeve formule i uranijumovih koeficijenata ... [ uranium @ 20.03.2006. 01:37 ] @
[ srki @ 20.03.2006. 03:18 ] @
Posto k1 mora da bude razlicito od nule onda to znaci da nisam lepo ubo formulu. Ali ona nejednakost sto sam naveo mora da vazi. To znaci da kada su l, m i n veliki i priblizno isti (ili recimo da jesu isti) onda je E priblizno 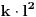 . Sada treba ubosti tacnu formulu. Mozda negde treba podeliti sa (l+m+n) ili tako nesto ali u svakom slucaju kada je l=m=n i kada je l veliko dobicemo priblizno . Sada treba ubosti tacnu formulu. Mozda negde treba podeliti sa (l+m+n) ili tako nesto ali u svakom slucaju kada je l=m=n i kada je l veliko dobicemo priblizno 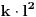 . .Citat: Možeš li da daš neko objašnjenje za onu procenu (nije mi očigledno zašto to mora da važi), a čak i kad bih znao zašto, ne bih nikad napravio toliko dobru pretpostavku o obliku f-je :-) Pogledaj http://mathworld.wolfram.com/RandomWalk2-Dimensional.html Takodje obrati paznju da je rastojanje od sredisnje tacke sigurno manje ili jednako od poluprecnika opisanog kruga oko trogugla a to 2(l+m+n). Minimalno rastojanje je min(l,m,n) a to znaci da je E vece od neke konstante pomnozene sa kvadratom tog rastojanja... Ako ti to nije dovoljno intiutivno onda pogledaj http://mathworld.wolfram.com/RandomWalk1-Dimensional.html gde ces videti da je za jednodimenzionalni random walk devijacija proporcionalna korenu iz N. Posto nas interesuje devijacija (tj. rastojanje od tezista) a ta devijacija u nasem slucaju je izmedju l i 2l onda sam izvukao onaj zakljucak. Naravno ovo je sve bez ikakvog matematickog dokaza, koristim samo intuiciju ali me nije stid jer je i Bojan rekao da se tako doslo do resenja :-) Citat: Da li nam teorema o rekurzivnoj f-ji garantuje jedinstvenost rešenja? Verovatno ne i zato kada nabodemo formulu treba uzeti i konkretne slucajeve (npr. 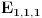 , , 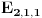 itd... itd...Mozda mozemo i bez ubadanja formule (Bojanov komentar me naveo da to pokusam) ali onda neko treba da smisli kako da resimo dvodimenzionalni random walk u trouglu. Da li neko ima volje da pokusa da resi onu rekurziju za 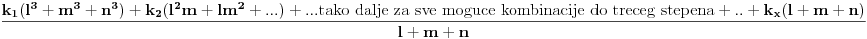 Bojane, da li mozes da nam kazes da li smo makar blizu resenja i da li je moja pretpostavka tacna da je za veliko l=m=n resenje priblizno 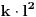 ? ?Imam jednu ideju kako da nadjemo formulu za l=m=n, sada cu da pokusam. Mislim da na slican nacin moze da se nadje i kada je l razlicito od m i n i m razlicito od n. Javicu sta sam uradio. [Ovu poruku je menjao srki dana 20.03.2006. u 06:36 GMT+1] [ uranium @ 20.03.2006. 05:49 ] @
@srki:
Zahvaljujem na objašnjenju - nažalost efekat je takav da mi je za sad jasna samo procena donje granice. Pročitao sam samo 2D slučaj ali ako sam dobro razumeo formula govori o ukupnom pređenom putu - tako da ipak još uvek ne kapiram onu gornju procenu... [ srki @ 20.03.2006. 07:06 ] @
Citat: uranium: ...ali ako sam dobro razumeo formula govori o ukupnom pređenom putu - tako da ipak još uvek ne kapiram onu gornju procenu... Ne, formula govori o krajnjem polozaju tacke (srednjoj vrednosti krajnjeg rastojanja tacke od pocetnog polozaja (devijacija)). Formula nam kaze koji je ocekivani broj koraka da tacka dosegne to rastojanje. Ukupan predjeni put je priblizno 2N*3/4 jer je 3/4 sansa da se tacka pomeri :-) E da, naravno da krajnji polozaj tacke ne znaci da tacka u toku puta nije otisla dalje ali opet i kada bismo racunali verovatnocu da nije otisla dalje mogli bismo videti da i ta verovatnoca ima slicnu raspodelu. O tome malo kasnije, idem sada kuci pa kada tamo stignem i veceram onda cu da probam da nastavim :-) [Ovu poruku je menjao srki dana 20.03.2006. u 10:49 GMT+1] [ uranium @ 20.03.2006. 07:31 ] @
Hvala srki - najzad i ja da shvatim
[ srki @ 20.03.2006. 10:25 ] @
Sada nesto petljam oko onog jednakostranicnog trougla i mislim da je uz pomoc njega moguce doci do resenja. Ali i pored toga imam jos jedan rezultat koji nekome moze pomoci. Sveo sam prethodno setanje broja novcica na najobicniji trodimenzionalni random walk.
Neka su  , ,  i i  trenutna novcana stanja prvog, drugog i treceg igraca. Uvedimo nezavisne promenjive trenutna novcana stanja prvog, drugog i treceg igraca. Uvedimo nezavisne promenjive  , ,  i i  tako da je tako da je 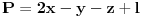 , , 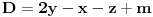 i i 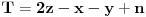 . Primetimo da ako povecamo jednu nezavisnu promenjivu za jedan da ce nam se odgovarajuce stanje jednog igraca povecati za dva a druga dva ce se smanjiti za 1. Na pocetku je . Primetimo da ako povecamo jednu nezavisnu promenjivu za jedan da ce nam se odgovarajuce stanje jednog igraca povecati za dva a druga dva ce se smanjiti za 1. Na pocetku je 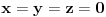 . U svakom koraku ili se ne dogodi nista ( . U svakom koraku ili se ne dogodi nista (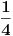 sanse) ili se jedna promenjiva poveca za 1. Kod ovoga je super sto su x, y i z potpuno nezavisne promenjive. Taj random walk je ogranicen sa sledece 3 ravni: sanse) ili se jedna promenjiva poveca za 1. Kod ovoga je super sto su x, y i z potpuno nezavisne promenjive. Taj random walk je ogranicen sa sledece 3 ravni: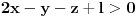 , ,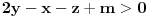 i 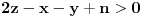 . .Sada treba resiti ovaj random walk i mozda vec postoje neke teorije u vezi sa tim ali ja se prvo bacam nazad na trougao. [ zzzz @ 21.03.2006. 00:12 ] @
Kritičan je igrač sa najmanje novčića "m" pa da vidimo kakve su mu šanse.
Odbacimo najprije sve jalove igre.Dodaćemo to na kraju priče. Šansa da se igra najbrže završi je da ovaj prvi zaredom stalno gubi. Tu vjerovatnost možemo izračunati.A možemo izračunati i vjerovatnost da nije izgubio u tom " m" koraku.Ako nije izgubio u tom koraku neće sigurno ni u sledeća dva.Može izgubiti tek u "m+3" koraku. Šansa da se i ovdje provuče je ista kao i prethodna! Umnožak ovih šansi je vjerovatnost da nije upao ni u "m+3" koraka. Itd itd sve dok ne postane kritičan i sledeći igrač.Tada moramo množiti i njegovu šansu da nije upao.Tj da nije ni jedan od njih upao. Idemo dalje od barijere do barijere.Kad stignemo do trećeg igrača uključimo u množenje i njegovu šansu da nije upao.Tjeramo tako dok umnožak ne bude manji od 0.5.Taj broj bacanja pomnožimo sa 4/3. (Izvinjavam se što sam koristio malo matematičkih izraza.Drugi put hoću. Kritična izjava je data bold.Meni tako ispada,a možda sam i promašio?) [ uranium @ 21.03.2006. 05:22 ] @
Evo koja je bila moja prva ideja u vezi sa ovim zadatkom.
Na osnovu one rekurzije, igra bi se mogla opisati sledećim beskonačnim regularnim grafom stepena 6 : [att_img] Koordinate čvorova govore o relativnoj promeni u broju novčića u odnosu na početno stanje. Zatim sam nameravao da nekako iskoristim onu rek. relaciju, ali napisanu malo drugačije: 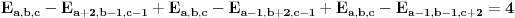 I hteo sam da to sumiram po svim mogućim trojkama 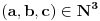 , uzimajući naravno , uzimajući naravno 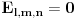 za za 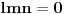 . Međutim, nešto se baš nisam snašao u nastavku . Međutim, nešto se baš nisam snašao u nastavku Još nešto, neka su početne vrednosti 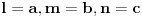 onda mi se čini da se sa slike jasno vide "linije" oblika onda mi se čini da se sa slike jasno vide "linije" oblika 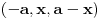 , , 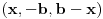 i i 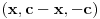 (u dodiru sa njima dolazi do prekida igre) pa bi možda neko mogao to da upotrebi (u dodiru sa njima dolazi do prekida igre) pa bi možda neko mogao to da upotrebi [Ovu poruku je menjao uranium dana 21.03.2006. u 06:58 GMT+1] [ peddja_stankovic @ 21.03.2006. 23:54 ] @
Za X123 (l=3, m=2, n=1) je lako naci raspodelu i ocekivanje
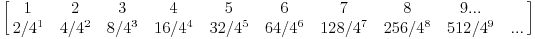 verovatnoca svakog sledeceg ishoda je "puta 2 i kroz 4"... Imam program koji racuna raspodele za bilo koji Xlmk Za X333 lako dobijam raspodelu 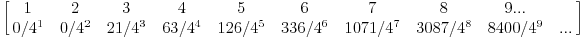 ali tu vec nije lako naci zakonitost da bih "analiticki resio ocekivanje. Imam takodje program koji racuna probliznu vrednost za bilo koji Xlmk sa tacnoscu na nekoliko decimala. Pokusao sam da iskoristim Uranium/Srki-jevu rekurentnu vezu. Lako dobijam Ea11, E222, E321. Vec za E333 imamo: 3E333 - 3E522 = 4 Ako bi nasli E522 lako bi nasli E333 Evo raspodele za X522 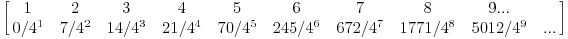 mozda nekom padne na um kako da nastavi niz 7, 14, 21, 70, 245, 672, 1771, 5012, ... [Ovu poruku je menjao peddja_stankovic dana 22.03.2006. u 01:02 GMT+1] [ uranium @ 22.03.2006. 01:23 ] @
Potražio sam nešto o tom nizu na sajtu On-Line Encyclopedia of Integer Sequences - ali nema ništa.
Poslao sam i pitanje jednom od njihovih robota, a šta mi je odgovorio pogledajte u prilogu Jedna njegova procena predviđa nastavak: [14427, 40642, 113729, 320250, 904057, 2547524] [ peddja_stankovic @ 22.03.2006. 05:58 ] @
To je to !!!
Ja sam imao te brojeve ali sam ih sacuvao za test. Hajde sad da vidimo sta cemo sa tim [ uranium @ 22.03.2006. 07:08 ] @
@peddja_stankovic:
Pa predlažem da odradiš to isto za još nekoliko vrednosti 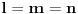 pa da šalješ robotu na svakih sat po jednu sekvencu pa da šalješ robotu na svakih sat po jednu sekvencu @srki: Na istom sajtu ima i dosta stvari u vezi sa random walk-om, pa možda iskopaš nešto korisno... [ peddja_stankovic @ 22.03.2006. 08:07 ] @
Nisam se bas nesto mnogo trudio da provalim ali ako je tebi jasno kako da iz
" -x+1+(x^3-3/7*x^2+3/7*x-1/7)*F(x) = 0 If this is correct the next 6 numbers in the sequence are: [14427, 40642, 113729, 320250, 904057, 2547524] " dobijem taj niz? [ uranium @ 22.03.2006. 08:37 ] @
[ peddja_stankovic @ 22.03.2006. 09:07 ] @
[ peddja_stankovic @ 24.03.2006. 18:53 ] @
Bice da je E333 = 36/7
E441 = 64/21 E522 = 80/21 Trebace mi malo vremena da postujem resenje [ peddja_stankovic @ 24.03.2006. 22:40 ] @
Malo sam iskompilirao ideje koje su se pojavile.
Srkijeva rekurencija i uranijumov graf. Kad dodamo malo 3D dolazimo do novih ideja. Na slici levo, imamo sve moguce ishode za slucaj l=m=n=3. Bela kockica nalazi se na (3,3,3) u Oxyz. To je pocetno stanje. Mozemo primetiti da broj ishoda koliko ko moze imati para uopste nije veliki. Moguce su samo [att_img] (3,3,3) - bela kockica, (5,2,2), (2,5,2), (2,2,5) - plave kockice, (4,4,1), (4,1,4), (1,4,4) - zelene kockice, (7,1,1), (1,7,1), (1,1,7) - zute kockice i crvene kockice koje upadaju u koordinatne ravni - tad se igra zavrsava (9,0,0), (0,9,0), (0,0,9), (6,3,0), (3,6,0), (6,0,3), (3,0,6), (0,6,3), (0,3,6). Vidimo da sve kockice leze u jednoj ravni, sto je i logicno jer je u svakom trenutku zbir novcica jednak 9. Sledi da su moguci ishodi na ravni x+y+z=9. (Mozemo vec unapred zakljuciti kad budemo radili opsti slucaj da svi ishodi leze u ravni x+y+z=l+m+n. Meni je zanimljivo to da postoje i neki ishodi ciji je zbir 9 a oni nisu u igri (na primer (1,2,6)). Ispada da je ovo random walk ali ne po nekom "kompaktnom" i kolicinom para ogranicenom 3d prostoru nego po nekom podskupu restrikovanim posebnim uslovima (tek treba da provalim sve detalje). Kasnije u tekstu cu poistovetiti srodne ishode. Na primer "(5,2,2), (2,5,2), (2,2,5) - plave kockice" ce mi biti dogadjaj 522 i slicno tako da na kraju imam samo dogadjaje 333, 522, 711, 411, 630, 900. Obratimo paznju na denu sliku. Odavde se vidi koji dogadjaj sledi iz kog dogadjaja. Sada ide glavno. Na osnovu ovog 3d grafa trebalo bi da je intuitivno jasno da vaze sledece relacije: 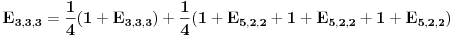 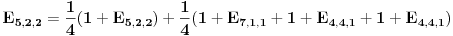 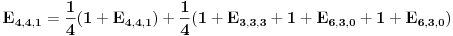 Dalje je 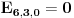 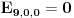 Vec smo dobili da je 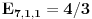 Resavanjem ovog sistema dobijamo 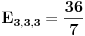 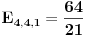 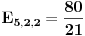 sto se potpuno slaze sa simulacijama koje sam do sada obavio. Cak vise me raduje da se metod moze lako uopstiti (bar se nadam). Prica sa generatorskom funcijom je moram priznati za mene nesto sasvim novo ali mi deluje uzasno interesantno jer sam citao malo o tome. Na zalost nisam uspeo resiti neke probleme u MCAD-u pa sam se vratio na stre ideje i za sada izgleda da nisam pogresio. Mala pauza i onda cu pokusati da uopstim proceduru. Ako je jos neko zainteresovan da pomogne, uvek je dobrodosla neka nova ideja. [Ovu poruku je menjao peddja_stankovic dana 24.03.2006. u 23:42 GMT+1] [ peddja_stankovic @ 26.03.2006. 13:01 ] @
Resavanjem sistema (vidi sliku)
[att_img] 4E444=E444+3E633+4 4E633=E633+2E552+E822+4 4E552=E552+2E741+E444+4 4E822=E822+2E741+E1011+4 4E741=E741+E633+E930+E660+4 4E1011=E1011+2E930+E1200+4 E930=0 E660=0 E1200=0 dobija se E444=128/15 E633=36/5 E552=20/3 E822=64/15 E741=56/15 E930=0 E1011=4/3 E660=0 E1200=0 Razmak izmedju svakog ishoda je koren iz 6. Sa slike vidimo da nisu svi ishodi "dvosmerni" [Ovu poruku je menjao peddja_stankovic dana 26.03.2006. u 17:07 GMT+1] [ peddja_stankovic @ 17.09.2008. 06:58 ] @
malo sam bio odsutan, jel moze da se dobije resenje zadatka
[ uranium @ 17.09.2008. 13:39 ] @
Evo jednog rešenja u prilogu - nadam se da je postavljač zadatka imao u vidu neki drugačiji pristup ... ;)
[ peddja_stankovic @ 17.09.2008. 18:10 ] @
pa da, to je to. sad proveravam sve ove pojedinacne rezultate koje sam dobio ali nisam dobio opstu formulu
dakle E(l,m,n)=4lmn/[3(l+m+n-2)] pogledacu ovih dana kako je resen problem. verujem da bi ja kad tad dosao do istog nego sam se smorio a i radio sam nesto drugo ovih dve godine. hvala za post [ Bojan Basic @ 19.09.2008. 22:54 ] @
Citat: uranium: Evo jednog rešenja u prilogu - nadam se da je postavljač zadatka imao u vidu neki drugačiji pristup ... Ne, upravo sam to imao u vidu, baš iz tog izvora. Otpade i ovaj zadatak s liste nerešenih. Obično ne postavljam rešenje dok se ne javi neko zainteresovan za dotično (ili, još bolje, dok ga neko ne reši), prosto zato što više volim da zadatak čeka potencijalnog rešavača nego da ga ja upropastim. Naravno, čim neko iskaže interesovanje za rešenje, kao sad Peđa, nije nikakav problem da ga postavim — s tim što me je ovaj put uranium pretekao. Nego, izgleda da Peđa nije jedini koji se vratio posle odsustva s foruma, je li? Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|