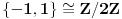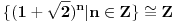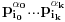[ devojcica @ 10.03.2006. 15:29 ] @
|
[ Bojan Basic @ 10.03.2006. 17:29 ] @
Citat: devojcica: Pokusavala sam da ih nadjem danima ali zaista ne znam na koji nacin to da ti dokazem? Imam nekoliko svedoka koji su me videli kako se mucim, ne znam, hoces da ti posaljem kontakt telefone da proveris? Ne trebaju mi kontakt telefoni, pretpostavljam da nisi tih nekoliko dana samo gledala u postavku već si verovatno nešto i skicirala sebi, pokušavala razne pristupe pa nisi uspela. Dovoljno je da napišeš samo 2-3 rečenice od toga pa makar ideja bila i potpuno pogrešna, poenta je da pokažeš da si se potrudila. Citat: devojcica: u svakom slucaju ne vidim kako moze da "steti kvalitetu foruma", "ne odgovara temi" ili krsi neko trece "pravilo"! Slažem se da ovaj tvoj jedan zadatak neće mnogo da šteti kvalitetu foruma, ali zar ne misliš da je u redu da imam jednake kriterijume prema svima? U suprotnom, ako bih tebi ostavio zadatak onda bi se neko bunio kad njemu obrišem i pitao kako to da sam tebi ostavio a njemu nisam, pa bih morao da ostavim i onom trećem, ukratko rečeno svima. Šta bismo dobili na kraju? Ovaj forum bi bio preplavljem lenjivcima (u potpunosti stojim iza ove reči) koji dođu iz škole, otvore svesku, prepišu domaći od reči do reči, nakon nekoliko sati se nakače i prepišu to što su dobili na tacni nazad u svesku, sutra pokažu profesoru kako oni to znaju da urade, i tako stalno. Ja to ovde neću da dozvolim, a (kad već pominješ pravila) sve što pričam postoji i sažeto ovde: Citat: 6. Ne tražite da Vam neko radi domaći zadatak Ne očekujte da bilo ko obavezno odradi sav posao umesto Vas! Rado ćemo pomoći oko svakog problema u slučaju da Vam "gori pod nogama", pred neki ispit ili posao, ali morate da pokažete na delu da ste u stvari krenuli sa radom i zastali pošto ne znate kako dalje. Nadam se da smo se ovoga puta bolje razumeli. [ SlavkoMoconja @ 13.03.2006. 17:05 ] @
Cao, devojcice!
Polja 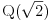 i i 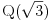 zadovoljavaju dati uslov. Naime: zadovoljavaju dati uslov. Naime:(1) 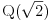 i i 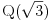 su neizomorfni: su neizomorfni:Ako pps (pretpostavimo suprotno) da 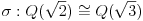 tada 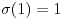 , i , i 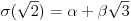 , za , za 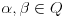 , pa , pa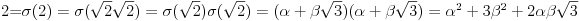 Iz linearne nezavisnosti 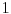 i i 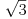 nad nad 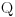 sledi da je sledi da je 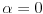 ili ili 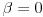 . Nijedan od ova dva slucaja nije moguc. Kontradikcija. Data polja su zaista neizomorfna. . Nijedan od ova dva slucaja nije moguc. Kontradikcija. Data polja su zaista neizomorfna.(2) 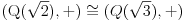 : :Sa 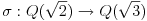 , definisano sa , definisano sa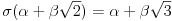 , je dat trazeni izomorfizam. , je dat trazeni izomorfizam.(3) 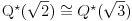 : :Pokazuje se da je 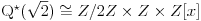 i i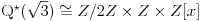 , pa su izomorfne. Ovo sledi iz toga da su prsteni , pa su izomorfne. Ovo sledi iz toga da su prsteni 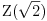 i i 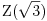 domeni sa jedinstvenom faktorizacijom, i vise, sve njihove jednote (invertibilni elementi) su oblika domeni sa jedinstvenom faktorizacijom, i vise, sve njihove jednote (invertibilni elementi) su oblika 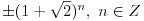 , odnosno , odnosno 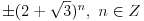 , pa je svaki element , pa je svaki element 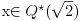 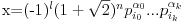 , gde , gde 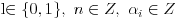 i i 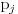 je niz medjusobno nekonjugovanih prostih brojeva, kojih ima beskonacno mnogo. Slicno vazi i za multiplikativnu grupu drugog polja. je niz medjusobno nekonjugovanih prostih brojeva, kojih ima beskonacno mnogo. Slicno vazi i za multiplikativnu grupu drugog polja.[ devojcica @ 18.03.2006. 10:27 ] @
[ devojcica @ 18.03.2006. 10:31 ] @
A evo i obrisanog zadatka:
Neka je K polje, f(x) i g(x) nerastavljivi separabilni polinomi nad K[x] stepena n, i  i i  redom koreni od f(x) i g(x) u redom koreni od f(x) i g(x) u 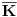 . Uocimo determinante . Uocimo determinante 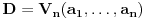 (Vandermondova determinanta reda n) i (Vandermondova determinanta reda n) i 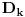 , , 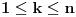 koje nastaju iz D zamenom k-te vrste sa koje nastaju iz D zamenom k-te vrste sa  . .Dokazati da je 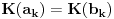 , za sve , za sve 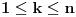 ako i samo ako je ako i samo ako je 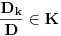 za sve za sve 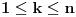 . .I ovaj je uspesno resen, postovacu i resenje ako ikoga zanima. [ milicas @ 18.03.2006. 14:57 ] @
Mene zanima. Postuj ako te ne mrzi
[ devojcica @ 19.03.2006. 11:59 ] @
<= :
Postavimo u 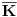 sistem jednacina: sistem jednacina: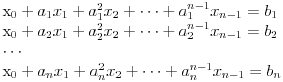 Matrica sistema je Van der Mondova, a matrice promenljivih su 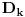 , pa su resenja , pa su resenja 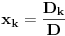 Imamo da je svako 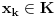 , pa je svako , pa je svako 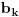 polinom po polinom po 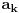 => 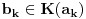 za svako k za svako k=> 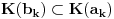 za svako k za svako kE sad, f(x) je nerastavljiv nad K, 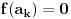 => f je minimalni polinom za 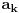 => Stepen rasirenja 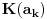 je n je nIsto tako, g je minimalni polinom za 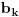 , pa je i stepen rasirenja , pa je i stepen rasirenja 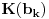 isto n. isto n.Oba rasirenja su istog stepena, jedno je podskup drugog => jednaka su 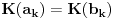 [ devojcica @ 19.03.2006. 12:59 ] @
=>:
Sada hocu nekako da napravim isti sistem, pazeci da mi koeficienti budu iz K. Imam da je 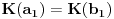 , rasirenja su stepena n , rasirenja su stepena n=> 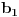 moze da se predstavi kao polinom po moze da se predstavi kao polinom po 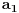 stepena n-1 nad poljem K. Neka je stepena n-1 nad poljem K. Neka je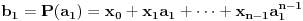 , ,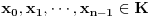 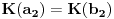 , rasirenja su stepena n , rasirenja su stepena n=> 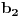 je polinom po je polinom po 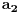 stepena n-1, samo jos ne znam da li je bas u pitanju isti polinom stepena n-1, samo jos ne znam da li je bas u pitanju isti polinom  . .Tj. hocu da pokazem da mi je i 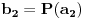 Koristimo Kronekerovu teoremu o ekstenziji: 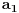 i i 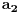 su nule istog polinoma nad K su nule istog polinoma nad K=> Postoji izomorfizam izmedju 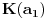 i i 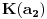 koji slika koji slika 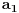 u u 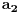 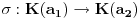 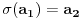 Pri tome, i nula polinoma g mora da se slika u nulu polinoma g (izvor: kolega Slavko :) ), pa je onda i 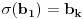 za neko k. Mislim da sada mozemo samo da preimenujemo za neko k. Mislim da sada mozemo samo da preimenujemo 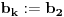 i i 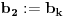 , pa je , pa je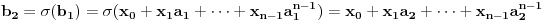 Ovim preimenovanjem mi se cuva osobina 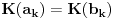 za svako k, i mislim da je to jedino vazno. za svako k, i mislim da je to jedino vazno.Analogno 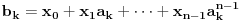 za svako k za svako k=> Imamo sistem: 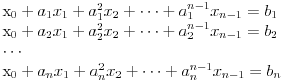 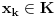 za svako k => za svako k =>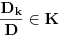 za svako k za svako k[ devojcica @ 19.03.2006. 13:02 ] @
@Slavko
Hajde objasni zasto se nula polinoma g slika u nulu polinoma g? [ SlavkoMoconja @ 19.03.2006. 14:23 ] @
Puno pitanja!
Ali evo. Najpre definicija nesvodljivog elementa je, ako je a=bc, tada b jednota, ili c jednota. Dakle u resenju mozemo uociti relaciju ekvivalencije a~b ako i samo ako a=ub, gde je u jednota. Tada kazemo da su ai b medjusobno konjugovani. Zasto je ono izomorfno prstenu Z[x]. (Izvinjavam se sto ovako pisem, ali me trenutno mrzi da se zezam sa texom). Pa ako proste(koji nisu medjusobno konjugovani) poredjamo u niz p0, p1,..., pn,... , tada sa fi (cini mi se da je bilo fi) element pi slikamo u x^i, a pi^a u ax^i. U Z[x] imamo samo konacne kombinacije, kao sto se svaki element moze predstaviti kao konacni proizvod stepena prostih(da li sam dobro rekao). Trece pitanje. Ako je g(a)=0, i f izomorfizam, tada kada na g(a)=0 delujemo sa f, imamo f(g(a))=f(0)=0. f je izomorfizam koji se poklapa sa identickim preslikavanjem na polju iz koga su koeficijenti polinoma g, pa ulazi pod polinom, tj. 0=g(f(a)). Odavde je jasno da je f(a) nula polinoma g. Jos jednom se izvinjavam zbog opisnih objasnjenja, ali stvarno me mrzi da pisem u texu. Pozdrav Milici i Marijani (devojcici). Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|