[ qzqzqz @ 14.03.2006. 19:59 ] @
| zanima me zasto iz tacnog tvrdjenja sledi uvek tacno tvrdjene? Jeste logicno ali da li postoji neki formalan matematicki dokaz toga? I uopste sta je tacno tvrdjenje? |
|
[ qzqzqz @ 14.03.2006. 19:59 ] @
[ Bojan Basic @ 14.03.2006. 20:31 ] @
Logika je oblast matematike. Kao što geometrija ima svoje aksiome tako i logika ima svoje aksiome, i svako logičko tvrđenje je ili aksiom ili se može izvesti iz konačno mnogo aksioma i pravila zaključivanja.
[ qzqzqz @ 14.03.2006. 21:10 ] @
e ta pravila zakljucivanje. kako znamo da mozemo tako da zakljucejemo zasto iz q sledi p
[ Bojan Basic @ 14.03.2006. 21:30 ] @
Evo malo detaljnije.
Aksiome: A1: 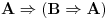 A2: 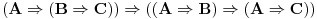 A3: 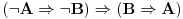 Pravilo izvođenja (modus ponens): 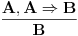 (donja formula je direktna posledica skupa gornjih formula) (donja formula je direktna posledica skupa gornjih formula)Za ove četiri stvari se ne pita zašto su tačne nego se jednostavno tako kaže. Sve ostalo se dokazuje preko njih. Može se napraviti i neka drugačija teorija ukoliko izmenimo nešto od gorenavedenog, a sadašnja iskazna logika je ovakva. [ cozi @ 18.03.2006. 21:19 ] @
Logika je oblast matematike, reci ovo na filozofskom fakultetu ako smes ;)
Jednostavno se podrazumeva da um(razum) funkcionise na taj nacin. [Ovu poruku je menjao cozi dana 18.03.2006. u 22:20 GMT+1] [ uranium @ 18.03.2006. 21:32 ] @
Mislim da bi se svaki pošten filozof složio da je Matematička logika najznačajniji deo savremene Logike.
Što se tiče početnog pitanja koje je postavio qzqzqz verujem da bi bilo zanimljivo pomenuti intuicionističku logiku, u kojoj recimo ne važi zakon isključenja trećeg - ali to je zato što se kod njih pojam istinitosti zamenjuje pojmom dokazivosti. [Ovu poruku je menjao uranium dana 18.03.2006. u 22:34 GMT+1] [ qzqzqz @ 21.03.2006. 14:20 ] @
e sad otkud znam da iz
 sledi sledi  . ne znam da li me razumete npr. Kako znamo da nema neki degenrisani pravougli trougao u kome ne vazi pitagorina teorem.. . ne znam da li me razumete npr. Kako znamo da nema neki degenrisani pravougli trougao u kome ne vazi pitagorina teorem..pr2. Naprimer ako 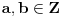 i i 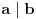 znaci znaci 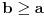 .E sad ako je .E sad ako je  , ,  to ne vazi. Zapravo vazi to ne vazi. Zapravo vazi 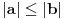 . Zar ne? E odgovor je ne npr b=0. . Zar ne? E odgovor je ne npr b=0.I jos nesto, sinoc sam se raspravljao nesto sa drugom. Da li postoji broj? Sta je broj i kako se definise?... [ Bojan Basic @ 21.03.2006. 20:41 ] @
Citat: cozi: Logika je oblast matematike, reci ovo na filozofskom fakultetu ako smes ;) Koliko god oni ne priznavali matematičku logiku, ja još više ne priznajem celu filozofiju (zajedno sa još mnogo toga) kao nauku. Zašto? Ne mogu da shvatim da se naukom može nazivati nešto što svaki tip koji se time bavi ima svoja shvatanja. U matematici (primera radi, naravno nije to jedina oblast) kad je nešto dokazano to svi matematičari prihvataju kao takvo i kraj priče. Po mom mišljenju (iako znam da je zapravo drugačije, niko mi ne brani da stvari shvatam kako ja hoću) jedino tako nešto može da se nazove naukom. Citat: To regulišeš aksiomima/teoremama iz odgovarajuće oblasti, recimo u tvom primeru iz teorije brojeva. [ cozi @ 21.03.2006. 23:41 ] @
ko ne priznaje matematicku logiku?
na filozofskom fakultetu se radi matematicka logika u okviru kursa logike. tesko da je filozofija nauka, siroka je to tema sta je danasnji pojam nauke i filozofije i njihov odnos. @qzqzqz posmatraj a sledi b kao iskaz i nista vise bice ti jasnije dakle a i b iz iskaza su u nekom odnosu koji je definisan u iskazu. pojam pravouglog trougla ne dozvoljava da ne vazi pitagorina teorema tako ako govoris o pravouglom trouglu govoris u strogo odredjenom smislu. poenta je kao sto je bojan napisao To regulišeš aksiomima/teoremama iz odgovarajuće oblasti mali oftopik zanimljivo je to da li postoji broj trougao, krug...recimo ne moze se zamisliti trougao uopste vec samo odredjeni pravougli ili nejednakostranicni ili jednakokraki... a opet ti trouglovi se ne mogu naci u prirodi(praksi)... [Ovu poruku je menjao cozi dana 22.03.2006. u 00:45 GMT+1] [ uranium @ 22.03.2006. 00:07 ] @
@cozi:
Da li bi mogao malo da pojasniš kako to ne može da se zamisli "trougao uopšte" (valjda misliš na generički pojam trougla) "već samo određeni"? Evo možeš to da mi objasniš na primeru da se ne može zamisliti filozofija uopšte nego samo neka konkretna To što se u prirodi (ma šta to bilo) ne može naći objekat koji odgovara nekom pojmu uopšte ne diskvalifikuje taj pojam. Opet: da li u prirodi postoje objekti koji odgovaraju pojmovima: filozofija, ljubav, mudrost... Matematički pojmovi su rezultat apstrakcije i rekao bih da najčešće govore o odnosima između objekata... [ qzqzqz @ 23.03.2006. 13:16 ] @
Citat: Bojan Basic: To regulišeš aksiomima/teoremama iz odgovarajuće oblasti, recimo u tvom primeru iz teorije brojeva. jel moze malo detaljnije? [ Bojan Basic @ 23.03.2006. 19:24 ] @
[ qzqzqz @ 23.03.2006. 19:56 ] @
[ Bojan Basic @ 23.03.2006. 20:33 ] @
Mislim da se sad već bolje razumemo. Za neki sistem aksioma (geometrija npr.) se pomoću drugih grana matematike može dokazati da je konzistentan, ali u opštem slučaju to nije moguće. Objašnjenje toga nam pruža Druga Gödelova teorema nekompletnosti. Jednostavno, formulišemo neki sistem aksioma i nadamo se da niko neće iz tog sistema dokazati tvrđenja i
 i i 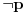 , a dok se to eventualno ne dogodi (za postojeće sisteme verovatnoća tako nečeg je, naravno, beskonačno mala) prihvatamo da ako pokažemo recimo da je , a dok se to eventualno ne dogodi (za postojeće sisteme verovatnoća tako nečeg je, naravno, beskonačno mala) prihvatamo da ako pokažemo recimo da je 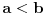 onda ne važi onda ne važi 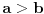 . .[ qzqzqz @ 24.03.2006. 13:58 ] @
znaci da bi dokazali da je neka teorija konzistenta moramo da uzmemo neke druge teorija. Kako cemo onda napraviti prvu konzistentu teoriju? I jel to znaci da mozda iz aksioma logike mozemo da izvedemo i negacije Gedelovih teorema?
Sad sam se uplasio.... [Ovu poruku je menjao qzqzqz dana 24.03.2006. u 14:59 GMT+1] [ Bojan Basic @ 24.03.2006. 14:16 ] @
Citat: qzqzqz: Kako cemo onda napraviti prvu konzistentu teoriju? Baš to pokušavam da ti kažem. Odgovor je nikako :) Citat: qzqzqz: I jel to znaci da mozda iz aksioma logike mozemo da izvedemo i negacije Gedelovih teorema? Možda, ne samo Gödelovih nego svih teorema, ali šanse za to su ravne nuli. Jednostavno živimo sa verom da su aksiome logike konzistentne zbog toga što niko do sada nije uspeo da dokaže suprotno. [ qzqzqz @ 24.03.2006. 14:40 ] @
Sta ce da bude ako se dodje do neke negacije teoreme? Cela matematika se obara(samim tim i sve sto postoji)? Misilm da je nemoguce da se matematika toliko razvijala, a da se nije doslo do kontradikcije. Verovatno tu postoji nesto cega covek nije svestan(misim kako matematika cuva samu sebe).
[Ovu poruku je menjao qzqzqz dana 24.03.2006. u 15:45 GMT+1] [ Lobacev @ 24.03.2006. 14:52 ] @
Srećom da Matematika ne mora da se čuva od svih nas.
[ Bojan Basic @ 24.03.2006. 15:32 ] @
Citat: qzqzqz: Sta ce da bude ako se dodje do neke negacije teoreme? Cela matematika se obara(samim tim i sve sto postoji)? Da :) Citat: qzqzqz: Misilm da je nemoguce da se matematika toliko razvijala, a da se nije doslo do kontradikcije. Upravo u tome je stvar, neko bi do sada došao do kontradikcije a kad već nije onda je najverovatnije nema. [ galet@world @ 28.03.2006. 18:38 ] @
Možda ovo šta ću da pitam ne spada na ovaj forum, ali zbog logike ipak ću se usuditi da postavim jedno jednostavno pitanje: Ako je α = β koliko je cos(α - β)? Molim vas da ovo ne shvatite kao šalu jer to zaista nije i dugo me muči. [ Nedeljko @ 28.03.2006. 23:43 ] @
Citat: qzqzqz: zanima me zasto iz tacnog tvrdjenja sledi uvek tacno tvrdjene? Jeste logicno ali da li postoji neki formalan matematicki dokaz toga? I uopste sta je tacno tvrdjenje? U iskaznom računu se istinitosna vrednost definiše za datu valuaciju (istinitosne vrednosti iskaznih slova) preko istinitosnih tablica. Logičke istine klasične iskazne logike su formule koje imaju istinitosnu vrednost tačno pri svakoj valuaciji. U predikatskom računu je stvar donekle slična, ali složenija. Formalan dokaz bi glasio ovako: Ako A ima istinitosnu vrednost tačno i A=>B ima istinitosnu vrednost tačno, onda na osnovu istinitosne tablice za implikaciju sledi da i B mora imati istinitosnu vrednost tačno. Ovde se pretpostavlja da radimo u nekoj teoriji baziranoj na klasičnoj logici, gde je prethodno definisana istinitost. Ovaj formalan dokaz je počiva na matematičkoj definiciji pojma "sledi". Kada se u matematici kaže da nešto sledi, misli se na to. Citat: cosi: Logika je oblast matematike, reci ovo na filozofskom fakultetu ako smes ;) Trenutni profesor logike na Filozofskom fakultetu Kosta Došen mi je jednom prilikom na ulici rekao da su logika i matematička logika sinonimi, i da je to naravno deo matematike. Citat: cosi: Jednostavno se podrazumeva da um(razum) funkcionise na taj nacin. Ne, to je greška koja se navodi u nekim lošim udžbenicima logike. Ljudskim umom se bavi psihologija. On ima svojih nesavršenstava. Logika se ne bavi zakonima u koje je ljudski um sklon da veruje zbog svoje nesavršenosti. Citat: Uranium: Mislim da bi se svaki pošten filozof složio da je Matematička logika najznačajniji deo savremene Logike. Skoro sigurno je u potpunosti tačno da je matematička logika daleko najrazvijeniji i najznačajniji deo savremene logike. Citat: Uranium: Što se tiče početnog pitanja koje je postavio qzqzqz verujem da bi bilo zanimljivo pomenuti intuicionističku logiku, u kojoj recimo ne važi zakon isključenja trećeg - ali to je zato što se kod njih pojam istinitosti zamenjuje pojmom dokazivosti. To je opšteprihvaćeno gledište na inuicionističku logiku. Međutim, ja se sa tim debelo ne slažem. Na jednom seminaru (doduše posvećenom teoriji skupova, koja nema prevelike veze sa intuicionističkom logikom) sam pričao o intuicionstičkoj logici. Bili su prikazani aksiomatika, Kripkeovi modeli, dokazi teorema saglasnosti i potpunosti aksiomatike u odnosu na modele, algoritmi za utvrđivanje da li je inuicionistička iskazna formula teorema inuicionističke iskazne logike, dokazi korektnosti, kompletnosti i zaustavljivosti tih algoitama i dokazi da neke formule nisu teoreme intuicionističke logike. Međutim, intuicionizam je bio izlagan u potpuno drugačijem duhu od onog koji se može naći u literaturi. Ja nemam nikakve primedbe na teoreme koje se odnose na inuicionizam, kao ni na dokaze tih teorema, već isključivo na njihovo tumačenje. Dakle, nemam niti jednu matematičku primedbu na ono što se piše o toj logici, već samo filozofske primedbe. Konkretno, ne slažem se sa tvrdnjama poput: "U inuicionističkoj logici ne važi zakon siključenaj trećeg." "Skup formula intuicionističke i klasične logike je isti." "Sve teoreme intuicionističke logike su teoreme klasične logike." "Postoje teoreme klasične logike koje nisu teoreme intuicionističke logike." "Intuicionistička logika je pravo suženje klasične logike." Smatram da su umesto njih tačne sledeće tvrdnje: "U intuicionističkoj logici važi zakon isključenja trećeg." "Skup formula intuicionističke logike je širi od skupa formula klasične logike." "Sve teoreme intuicionističke logike koje su na jeziku klasične logike su teoreme klasične logike. Međutim, jezik intuicionističke logike je širi od jezika klasične logike, pa teoreme intuicionističke logike koje nisu na jeziku klasične logike (a takve postoje) svakako ne mogu biti teoreme klasične logike." "Sve teoreme klasične logike jesu teoreme intuicionističke logike." "Intuicionistička logika je pravo proširenje klasične logike." Osećam da ćete me streljati zbog ovoga. Citat: qzqzqz: Kako znamo da nema neki degenrisani pravougli trougao u kome ne vazi pitagorina teorem.. Upravo tome služi dokaz Pitagorine teoreme. On ne pretpostavlja ništa drugo o trouglu, osim da je pravougli. Upravo je u tome smisao dokaza matematičkih teorema. Svi slučajevi moraju biti obuhvaćeni. Citat: qzqzqz: Da li postoji broj? Sta je broj i kako se definise?... Lično mi nije poznato da u matematici postoji pojam koji se zove broj. Postoje pojmovi koji u svom nazivu sadrže reč broj (realni brojevi, prirodni brojevi itd.), i ti pojmovi su precizno definisani, ali mi u matematici nije poznat pojam čije je "puno ime i prezime" baš "broj". Često se termin broj koristi kao skraćenica za neki od pojmova koji u nazivu sadrže reč broj, kada je iz konteksta jasno na šta se misli. Citat: Bojan Basic: Koliko god oni ne priznavali matematičku logiku, ja još više ne priznajem celu filozofiju (zajedno sa još mnogo toga) kao nauku. Zašto? Ne mogu da shvatim da se naukom može nazivati nešto što svaki tip koji se time bavi ima svoja shvatanja. U matematici (primera radi, naravno nije to jedina oblast) kad je nešto dokazano to svi matematičari prihvataju kao takvo i kraj priče. Po mom mišljenju (iako znam da je zapravo drugačije, niko mi ne brani da stvari shvatam kako ja hoću) jedino tako nešto može da se nazove naukom. Nijedan filozof neće reći za filozofiju da je nauka. Filozofija se upravo bavi pitanjima na koje naučni metod nije primenljiv zbog svojih ograničenja. Na ta pitanja ne postoji samo jedan odgovor. Filozofi često uobražavaju da je filozovija nešto iznad nauke. Istina je da je prednost naučnog metoda što je pouzdaniji, a da mu je nedostatak što ima kraći domet. Isto tako je matematički metod pouzdaniji od naučnog, ali ima kraći domet. Preciznija puška manje daleko dobacuje. Citat: Uranium: Matematički pojmovi su rezultat apstrakcije i rekao bih da najčešće govore o odnosima između objekata... Matematika se bavi pronalaženjem zaključivanja koja imaju deduktivnu snagu. Jedna od definicija dedukcije je da je to zaključivnje koje je tačno pri budi bilo kakvim interpretacijama polaynih pojmova. Stoga je sasvim svejedno kako ćeš da zamišljaš, ili interpretiraš polazne matematičke pojmove. Interpretacijama polaznih pojmova su potpuno određene interpretacije izvedenih pojmova. Citat: qzqzqz: Kako cemo onda napraviti prvu konzistentu teoriju? Mora od nečega da se pođe. Ne možeš se izvući iz živog blata vukući sam sebe za uši. Citat: qzqzqz: Sta ce da bude ako se dodje do neke negacije teoreme? Cela matematika se obara(samim tim i sve sto postoji)? To će značiti da barem jedan od polaznih matematičkih principa nije bio dobar. U tom slučaju bi se bar jedan od tih principa morao odbaciti ili oslabiti. Nakon toga bi cela matematika morala da se revidira. Upravo se to desilo i XIX veku sa naivnom teorijom skupova, tada mladom teorijom. Citat: qzqzqz: Misilm da je nemoguce da se matematika toliko razvijala, a da se nije doslo do kontradikcije. Verovatno tu postoji nesto cega covek nije svestan(misim kako matematika cuva samu sebe). Postoje dve mogućnosti: da kontradikcije nema, ili da su ljudi bili glupi da je do sada nisu uspeli da je pronađu. U prvom slučaju se i ne može izvesti kontradikcija. Međutim, prema Gedelovim teoremama nepotpunosti, u om slučaju mi nemožemo znati da je upravo to slučaj. Sa druge strane, ako kontradikcije ima, onda je moguće saznati da je ima. Citat: galet@world: Ako je α = β koliko je cos(α - β)? Siguran sam da znaš šta mislimo o tome. Ako imaš neke primedbe na taj odgovor, onda je tvoj posao da ih izneseš. [ uranium @ 29.03.2006. 00:11 ] @
Citat: Nedeljko: Osećam da ćete me streljati zbog ovoga. To bi bila neprocenjiva šteta Umesto toga, evo ja bih te zamolio da npr. malo detaljnije obrazložiš onaj deo o isključenju trećeg - ili da daš neku pristupačnu (ne samo fizički [ Nedeljko @ 29.03.2006. 01:07 ] @
Referencu dajem u prilogu. Nikakve teoreme nisam dokazivao. Sav matematički deo je poznat svakome ko se ozbiljnije bavio intuicionizmom. Tu nemam nikavih ni primedbi, niti inovacija. Ovo nisam nigde video, pa nemam nijednu referencu koju nisam ja pisao.
[ Nedeljko @ 29.03.2006. 01:10 ] @
Citat: uranium: da daš neku pristupačnu (ne samo fizički :)) referencu... A šta to znači "nefizički pristupačna referenca"? [ uranium @ 29.03.2006. 03:42 ] @
Mislio sam na pristupačnost u smislu potrebnog predznanja.
Nadam se da je ono "nefizički" šala u vezi sa z.i.t. Najiskrenije se zahvaljujem na onom materijalu, ali sad imamo dve mogućnosti: 1. Ako se držiš definicije intuicionističke logike, onda je smisao formule 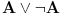 potpuno promenjen - pa se ona više ni ne može smatrati zakonom isključenja trećeg, jer ona više ne znači: dokazivo je potpuno promenjen - pa se ona više ni ne može smatrati zakonom isključenja trećeg, jer ona više ne znači: dokazivo je  ili je dokazivo ili je dokazivo 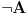 , nego sad znači: , nego sad znači: 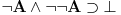 a u opštem slučaju ne važi a u opštem slučaju ne važi 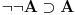 . .2. Odlučio si da promeniš definiciju int. logike - onda je sve u redu - napravio si proširenje klasične logike i nikom ništa Da li se neki član "skupa" {K.D., Ž.M., S.P, M.K., Z.M.} usprotivio ovakvom tvom gledištu? [ galet@world @ 29.03.2006. 08:35 ] @
Citat: Nedeljko: Siguran sam da znaš šta mislimo o tome. Ako imaš neke primedbe na taj odgovor, onda je tvoj posao da ih izneseš. Znam samo šta ti misliš o tome, ali da odradim moj “posao” Ako na primer ugao od 10 podelimo na beskonačno mnogo delova dobićemo ugao od 00 . Takav ugao postoji i ima dimenziju izraženu u stepenima. Ako od nekog ugla oduzmemo isti takav ugao dobićemo rezultat 0, međutim, ova nula se suštinski razlikuje od prethodne, jer ovakva nula ne može imati nikakvu dimenziju, jer baš sve što smo imali to smo i oduzeli. Ovakvu nulu bih ja nazvao “apsolutnom” nulom jer ona znači nepostojanje. Oduzeti od neke vrednosti istu takvu vrednost znači isto što i ukloniti ili uništiti. Ta vrednost više ne postoji – u konkretnom slučaju ne postoji više ugao. Moj zaključak je da govoriti o kosinusu takve nule nema smisla jer je to isto što i govoriti o kosinusu nepostojećeg ugla. Budući da znam šta o tome misli autor gornjeg citata zamolio bih ga da se ovaj put uzdrži, da bi mogli da čujemo i druge. [ Nedeljko @ 29.03.2006. 09:44 ] @
Nadam se da se ipak nećeš ljutiti ako i ovde napišem svoje mišljenje, mada sam ga napisao i na forumu za fiziku. To i dalje ne sprečava ostale učesnike da i oni iznesu svoja mišljenja.
Uz to, pisanje oznake za stepen ovde samo zbunjuje, jer se meša sa stepenovanjem na nulu. Bolje je stepen pisati rečima. Pokušaj takvu podelu ugla da opišeš geometrijski, pa da vidimo šta su kraci takvih delova (ili jednog od tih delova). Veruj mi da se trudim da budem krajnje konstruktivan. Ako se koristi zasnivanje realnih brojeva kao kompletnog uređenog polja, i ravni preko realnih bropjeva, u tom polju neće biti beskonačno malih veličina, pa samim tim ni u toj ravni beskonačno bliskih tačaka, krakova itd. U tom slučaju treba da definišeš tu beskonačnu podelu o kojoj govoriš. Ako pak koristimo neko nearhimedovsko polje kao zasnivanje realnih brojeva, dakle uređeno polje koje uključuje infinitezimale, onda tu zajedno sa beskonačno malim veličinama imamo i beskonačno velike, uključujući i beskonačno velike prirodne brojeve (zovu se nestandardni), koji su u svemu ravnopravni sa konačnim. Svaki ugao se može podeliti na n jednakih delova, za svaki prirodan broj n, koji u ovom slučaju može biti i beskonačan, pa je rezultat delenja podela na beskonačno mnogo beskonačno malih uglova. U matematici se pod nulom podrazumeva neitralni element za sabiranje, koji je jedinstven. Drugim rečima, nula je u matematici samo to što ti nazivaš "apsolutnom nulom", a beskonačno male veličine su nešto drugo. Nema nikakve potrebe menjati standardnu terminologiju, pa infinitezimale zvati nulama, a amnulu apsolunim nulama, jer se promenom termina u sadržaju ništa ne menja, a sa druge strane se otežava komunikacija. Standardne pojmove treba nazivati standardnim terminima, a za nove pojmove uvoditi nove termine. Ugao je u matematici oblast u ravni čiju granicu čine dve (zatvorene) poluprave sa zajedničkim temenom. Ako se uglovi mere u stepenima, onda ugao mora imati meru koja je veća od nule, a manja od 360. Ugao od nula stepeni ne postoji. Odgovarajuća prazna oblast se ne smatra uglom. Kosinus kao funkcija na uglovima se definiše kao funkcija koja uglovima pridružuje realne brojeve, pa shodno tome, kosinus ugla od nula stepeni ne postoji, jer takav ugao ne postoji. Sa druge strane, kosinus beskonačno malog ugla postoji, manji je od jedan i beskonačno blizak jedinici. No, o tome se može govoriti samo u svetlosti nearhimedovskih polja. Sa druge strane, kosinus kao funkcija na realnim (ili kompleksnim) brojevima se definiše kao funkcija koja svakom realnom (ili kompleksnom) broju pridružuje realan (ili kompleksan) broj. Treba je razlikovati od funkcije kosinusa ugla. To su različite funkcije jer im je domen različit. Definicija ovog drugog kosinusa može na primer da bude 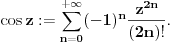 Tu je 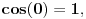 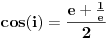 itd. itd.[ Nedeljko @ 30.03.2006. 00:59 ] @
Citat: Izvini što ovako kasno odgovaram. Sve do sad nisam video tvoju poruku. Ne, nisam ja promenio definiciju intuicionističke logike, jer to onda ne bi bila intuicionistička, već neka druga logika. Samo sam izabrao sistem oznaka u kome neće dolaziti do zabune usled označavanja različitih pojmova istim oznakama. Radi se o sledećem: Ako formula oblika 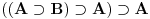 u opštem slučaju nije teorema, onda u opštem slučaju nije teorema, onda 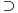 nije oznaka za (klasičnu) implikaciju, već je to sasvim drugi logički veznik. Ne razlikuju se u logici veznici po oznakama, već po zakonima koji za njih važe. Neće neki veznik postati implikacija samo zato što ga je neko označio strelicom udesno. Ja sam samo označio različite logičke veznike različitim simbolima. nije oznaka za (klasičnu) implikaciju, već je to sasvim drugi logički veznik. Ne razlikuju se u logici veznici po oznakama, već po zakonima koji za njih važe. Neće neki veznik postati implikacija samo zato što ga je neko označio strelicom udesno. Ja sam samo označio različite logičke veznike različitim simbolima.Zakon isključenja trećeg nikada nije glasio "dokazivo je A ili je oborivo A". On glasi: "Jeste A ili nije A". U protivnom bi ga bilo nemoguće formulisati u klasičnoj logici. Ipak je on potekao iz klasične logike. Zakon isključenja trećeg glasi: 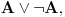 gde je gde je 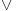 oznaka za (klasičnu) disjunkciju. Ako umesto njega stavim negi drugi logički veznik, onda to više nije zakon isključenja trećeg. Po čemu imam pravo da stavim umesto njega intuicionističku disjunkciju, i da to i dalje zovem zakonom isključenja trećeg, a nemam pravo da stavim, na primer konjunkciju, pa da i formulu oznaka za (klasičnu) disjunkciju. Ako umesto njega stavim negi drugi logički veznik, onda to više nije zakon isključenja trećeg. Po čemu imam pravo da stavim umesto njega intuicionističku disjunkciju, i da to i dalje zovem zakonom isključenja trećeg, a nemam pravo da stavim, na primer konjunkciju, pa da i formulu 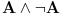 zovem "zakonom isključenaj trećeg za konjunkciju", i isto tako za implikaciju, ekvivalčenciju. zovem "zakonom isključenaj trećeg za konjunkciju", i isto tako za implikaciju, ekvivalčenciju.Nazivanje zakona "A je dokazivo ili oborivo" zakonom isključenja trećeg je menjanje prvobitnog smisla tog zakona. Ja sam se nasuprot tome držao originalne formulacije tog zakona. Isto tako "postojanje" i "konstruktibilnost" nisu isti pojmovi, pa ni pomenuti kvantifikatori nisu isti. Zbog čega da ih mešam označavajući ih istim oznakama. Ne vidim niti jednu prednost takvog pristupa. Nasuprot tome, on sakriva sučtinu intuicionističke logike. Citat: uranium: Da li se neki član "skupa" {K.D., Ž.M., S.P, M.K., Z.M.} usprotivio ovakvom tvom gledištu? Usprotivio se P.J. Ne znam da li je kasnije prihvatio. Prihvatili su S.P. i A.J. Takođe, tekst je upravo na čitanju kod Z.O., ali mi još nije odgovorio. Sa ovima ostalima nisam razgovarao. Citat: uranium: Nadam se da je ono "nefizički" šala u vezi sa z.i.t A šta je sad pa z.i.t? [ uranium @ 30.03.2006. 03:51 ] @
U onom tvom materijalu sam veznik
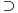 i shvatio kao potpuno novi veznik, ali sam u mom prethodnom postu taj veznik upotrebio u standarnom intuicionističkom smislu tj. kao implikaciju - ali sam zaboravio da to napomenem - izvini zbog toga. i shvatio kao potpuno novi veznik, ali sam u mom prethodnom postu taj veznik upotrebio u standarnom intuicionističkom smislu tj. kao implikaciju - ali sam zaboravio da to napomenem - izvini zbog toga.U intuicionističkoj logici je bitno da imaš konstrukciju kojom dokazuješ neko tvrđenje tako da u strogom smislu ne možemo ni govoriti o z.i.t. (zakonu isključenja trećeg) u izvornom, nego u prilagođenom obliku. Ovi stavovi počivaju na uverenju da u int. logici nema mesta pojmovima: jeste, nije, istina, laž - već pojmovima dokaziv, oboriv. Formalno gledano, možemo da zažmurimo na ovu razliku - ali onda ne možemo istovremeno da pričamo o obe teorije (osim čisto sintaksno). Ali ti sad pokušavaš da napraviš klasičnu logiku unutar intuicionističke u kojoj je 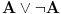 teorema, ali to više nema smisao koji ima u pravoj klasičnoj logici - u protivnom niko nikad ne bi ni tvrdio da u int. logici "ne važi z.i.t.". teorema, ali to više nema smisao koji ima u pravoj klasičnoj logici - u protivnom niko nikad ne bi ni tvrdio da u int. logici "ne važi z.i.t.". Dakle, kao što si i sam napisao - ako nam je kriterijum razlikovanja veznika, skup zakona koji važe za njih - jedina formula koju bi imali pravo da zovemo z.i.t. je 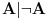 a za nju znamo da ne važi. a za nju znamo da ne važi.[ Nedeljko @ 30.03.2006. 08:56 ] @
Citat: uranium: ali sam u mom prethodnom postu taj veznik upotrebio u standarnom intuicionističkom smislu tj. kao implikaciju Implikacija je veznik klasične logike. Problem je upravo u onom "u intuicionističkom smislu, tj. kao implikaciju", gde se intuicionistička implikacija, koja nije implikacija, jer ne zadovoljava zakon 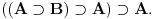 Hoću da kažem sledeće: jedan veznik je implikacija, a drugi veznik je intuicionistička implikacija. Kada se ne kaže drugačije, implikacija je klasična. U svakom slučaju, ti veznici (koji su različiti) ne smeju da se mešaju. Hoću da kažem sledeće: jedan veznik je implikacija, a drugi veznik je intuicionistička implikacija. Kada se ne kaže drugačije, implikacija je klasična. U svakom slučaju, ti veznici (koji su različiti) ne smeju da se mešaju.Citat: uranium: U intuicionističkoj logici je bitno da imaš konstrukciju kojom dokazuješ neko tvrđenje Zavisi od tvrđenja koje dokazuješ. Bitno je da pronađeš term  za koji možeš da dokažeš za koji možeš da dokažeš 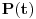 ako dokazuješ tvrđenje ako dokazuješ tvrđenje 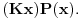 Ukoliko dokazuješ formulu Ukoliko dokazuješ formulu 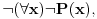 onda ti pronalaženje takvog terma nije bitno. Prva formula odgovara zadatku "Naći x za koje važi P(x)", i tada si po prirodi zadatka obavezan da nažeš takav objekat, i intuicionistička logika te zaista obavezuje na to. Druga formula odgovara zadatku "Dokazato da postoji x za koje je P(x)". Po prirodi zadatka pronalaženje takvog x nije obavezujuće u rešenju, i intuicionistička logika te zaista ne obavezuje na to u dokazivanju one druge formule. onda ti pronalaženje takvog terma nije bitno. Prva formula odgovara zadatku "Naći x za koje važi P(x)", i tada si po prirodi zadatka obavezan da nažeš takav objekat, i intuicionistička logika te zaista obavezuje na to. Druga formula odgovara zadatku "Dokazato da postoji x za koje je P(x)". Po prirodi zadatka pronalaženje takvog x nije obavezujuće u rešenju, i intuicionistička logika te zaista ne obavezuje na to u dokazivanju one druge formule.Citat: uranium: u strogom smislu ne možemo ni govoriti o z.i.t. (zakonu isključenja trećeg) u izvornom, nego u prilagođenom obliku. Naprotiv, možemo govoriti o z.i.t., zato što su svi klasični veznici definljivi u intuicionističkoj logici. Citat: uranium: Ovi stavovi počivaju na uverenju da u int. logici nema mesta pojmovima: jeste, nije, istina, laž - već pojmovima dokaziv, oboriv. Koncepti "istine" i "laži" su samo jedan način gledanja na klasičnu logiku. Oni jesu najjednostavniji i dovoljno dobri kada se govori samo o klasičnoj logici, ali po pravilu nisu dovoljno dobri u proširenjima klasične logike. Bitni su skup formula i skup teorema. Citat: uranium: Formalno gledano, možemo da zažmurimo na ovu razliku - ali onda ne možemo istovremeno da pričamo o obe teorije (osim čisto sintaksno). A zašto nemožemo, ako je jedna teorija podteorija druge teorije? Citat: Definljivost klasičnih veznika u intuicionističkoj logici je teorema koju nisam ja dokazao, već drugi mnogo pre nego što sam se ja ispilio. Drugo, ne postoji "klasična logika" u kojoj nije 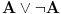 teoema. Dovoljno je bilo da kažeš "praviš klasičnu logiku unutar intuicionističke". Dodatak sa formulom koju si naveo je suvišan. No, nije bitno. Ne sumnjam da to i sam znaš. teoema. Dovoljno je bilo da kažeš "praviš klasičnu logiku unutar intuicionističke". Dodatak sa formulom koju si naveo je suvišan. No, nije bitno. Ne sumnjam da to i sam znaš.Citat: uranium: ali to više nema smisao koji ima u pravoj klasičnoj logici Pojam "smisla" nije matematički. Za logike se kaže da su iste ako imaju isti skup formula i isti skup teorema. I klasičnu logiku može uvesti, čak i modelski, bez dvovrednosnih istinitosnih tablica. Možeš preko bulovsko vrednosnih modela, ili preko semantičkih tabloa, ili na ko zna koje druge načine. Niko te ne tera da koristiš baš dvočlanu Bulovu algebru. Međutim, biće reč o istoj logici jer je skup formula isti, i skup teorema isti. Citat: uranium: u protivnom niko nikad ne bi ni tvrdio da u int. logici "ne važi z.i.t.". Pa, ja i ne tvrdim da ne važi. Moje uverenje je upravo da važi. Za druge ne odgovaram. Citat: Upravo sam zbog ovoga izbegavao zakon isključenja trećeg i išao na Pirsov zakon. U njemu se pojavljuje samo jedan logički veznik: implikacija. U aksiomatizaciji kasične logike koju sam naveo se zakon isključenja trećeg može zameniti Pirsovim zakonom. Dobiće se ekvivalentna aksiomatizacija. U zakonu isključenja trećeg imamo dva logička veznika: disjunkciju i negaciju. No, sada i ovo moram da obrazložim. Ako izolovano posmatramo logičke veznike 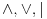 (svaki ponaosob bez ostalih veznika) skup teorema na jeziku svakog od tih veznika pojedinačno je isti. To je prazan skup formula. Ne postoji niti jedna tautologija samo samo na jeziku konjunkcije, niti samo na jeziku disjunkcije, niti postoji intuicionistička teorema samo na jeziku intuicionističke disjunkcije (to jest, da se u njoj pojavljuju samo iskazna slova, zagrade i intuicionistička disjunkcija). Sa te strane se navedeni veznici ne razlikuju. Obrati pažnju da su i konjunkcija i disjunkcija u klasičnoj logici izolovano gledano jedan te istli logički veznik. Oni se razlikuju tek u kombinaciji sa drugim logičkim veznicima. (svaki ponaosob bez ostalih veznika) skup teorema na jeziku svakog od tih veznika pojedinačno je isti. To je prazan skup formula. Ne postoji niti jedna tautologija samo samo na jeziku konjunkcije, niti samo na jeziku disjunkcije, niti postoji intuicionistička teorema samo na jeziku intuicionističke disjunkcije (to jest, da se u njoj pojavljuju samo iskazna slova, zagrade i intuicionistička disjunkcija). Sa te strane se navedeni veznici ne razlikuju. Obrati pažnju da su i konjunkcija i disjunkcija u klasičnoj logici izolovano gledano jedan te istli logički veznik. Oni se razlikuju tek u kombinaciji sa drugim logičkim veznicima.Zbog toga se takav koncept poređenja proširuje sa veznika na sisteme veznika. Sistem veznika 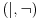 ne odgovara sistemu (disjunkcija,negacija) upravo zbog toga što formula ne odgovara sistemu (disjunkcija,negacija) upravo zbog toga što formula 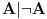 nije teorema. Izolovano gledano, nije teorema. Izolovano gledano,  jeste disjunkcija i jeste disjunkcija i  jeste negacija. Isto tako je izolovano posmatrano i jeste negacija. Isto tako je izolovano posmatrano i 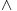 disjunkcija. Da li zbog toga smatraš da je disjunkcija. Da li zbog toga smatraš da je 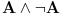 takođe zakon isključenja trećeg? Razmotri ovu svoju primedbu na primeru Pirsovog zakona. Jasnije je, jer imaš samo jedan logički veznik u igri. takođe zakon isključenja trećeg? Razmotri ovu svoju primedbu na primeru Pirsovog zakona. Jasnije je, jer imaš samo jedan logički veznik u igri.[ uranium @ 30.03.2006. 10:57 ] @
Citat: Nedeljko: Hoću da kažem sledeće: jedan veznik je implikacija, a drugi veznik je intuicionistička implikacija. Kada se ne kaže drugačije, implikacija je klasična. U svakom slučaju, ti veznici (koji su različiti) ne smeju da se mešaju. Pa zato sam i upotrebio oznaku 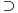 . .Citat: Nedeljko:Zavisi od tvrđenja koje dokazuješ. Slažem se, ali ovde je od interesa bio z.i.t. a on nije oblika o kome pričaš. Citat: Nedeljko:Naprotiv, možemo govoriti o z.i.t., zato što su svi klasični veznici definljivi u intuicionističkoj logici. Da je to stvarno tako, ne bi ni bilo razlike između klasične i int. logike - seti se da si i sam više puta rekao da su međusobni odnosi veznika ono što ih određuje. Npr. već pomenutu implikaciju nije moguće definisati u int. logici - i sam si lepo objasnio zašto (ono kako si ti definisao "klasičnu" implikaciju ne mogu da računam iz prethodno pominjanih razloga). Nisam to ni napisao - već sam napisao to da si ti napravio da to bude teorema u tvojoj "int. logici". I to na osnovu definicije disjunkcije i jeste teorema ali to ne možeš zvati zakonom isključenja trećeg. Hajde da raščistimo jednu stvar: da li se slažeš da je u int. logici 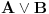 dokazano, samo ako se može dati (u opštem slučaju) konstrukcija iz koje se može zaključiti koja od tih formula je dokaziva i ne samo to već i njen (u opštem slučaju konstruktivan) dokaz. Pogledaj šta si svojevremeno napisao. dokazano, samo ako se može dati (u opštem slučaju) konstrukcija iz koje se može zaključiti koja od tih formula je dokaziva i ne samo to već i njen (u opštem slučaju konstruktivan) dokaz. Pogledaj šta si svojevremeno napisao.Citat: Nedeljko: Pojam "smisla" nije matematički. Je l' ja sad treba da kažem da ova tvoja rečenica nije teorema? Uopšte ne razumem zašto pominješ Pirsov zakon kada ni on ne važi (opet naglašavam da tvoju definiciju implikacije ne mogu da prihvatim za klasičnu ili ako više voliš - ono što si ti napravio ne mogu da prihvatim za intuicionističku logiku). Postoji još čitav niz stavova sa kojima se ne slažem, ali je to sekundarnog značaja Da li nameravaš negde da objaviš ta zapažanja. Voleo bih da nam eventualno preneseš mišljenja recenzenata. Na kraju, mislim da shvatam tvoje gledište, ali za sada ne mogu da se složim sa njim. [ Nedeljko @ 30.03.2006. 14:36 ] @
Možda me utisak vara, ali čini mi se da si se u poslednjoj poruci nekako "naoštrio". Ipak se nadam da diskusija teče bez emotivnih naboja. Ranije smo se poštovali, i nadam se da se tu ništa nije promenilo, kao i da će tako ostati ubuduće. Smatram da nema nikakvih razloga da bude drugačije.
Da upotrebio si je, ali uz, za mene neprihvatljiv komentar "u standarnom intuicionističkom smislu tj. kao implikaciju". Koju implikaciju. Ja pod "implikacijom" podrazumevam samo klasičnu implikaciju. Za svaku drugu navodim njeno "puno ime i prezime". Dakle, u toj aksiomatici simbol 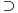 nije oznaka za implikaciju, već za intuicionističku implikaciju, koja je sasvim drugi logički veznik. nije oznaka za implikaciju, već za intuicionističku implikaciju, koja je sasvim drugi logički veznik.Nekako stičem utisak (mada ne mogu da tvrdim, da ne budem pogrešno shvaćen) kao da čitaš samo moje odgovore, a ne i citate koje navodim uz odgovore. Njih navodim da bih pojasnio na šta se moji odgovori odnose, i smatram da je njihovo čitanje važno za bolje razumevanje tih odgovora. Možda grešim, nemoj da se ljutiš. Ti to znaš najbolje. No, u svakom slučaju, čitaj i citate. Citat: uranium: Slažem se, ali ovde je od interesa bio z.i.t. a on nije oblika o kome pričaš. A šta je zakon isključenja trećeg? Kako on glasi? Da li je 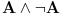 zakon isključenja trećeg? Da li zakon isključenja trećeg može da glasi zakon isključenja trećeg? Da li zakon isključenja trećeg može da glasi 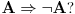 Ne mogu da prihvatim Ne mogu da prihvatim 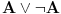 kao zakon isključenja trećeg, ako se ne kaže šta znače upotrebljene oznake. Ovde mislim pre svega na simbol kao zakon isključenja trećeg, ako se ne kaže šta znače upotrebljene oznake. Ovde mislim pre svega na simbol 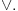 Lično smatram da nije bitno koje oznake koristimo, nego sadržaj tvrđenja o kome govorimo. Možda je ipak bolje da se vratimo na Pirsov zakon, pošto u njemu figuriše samo jedan logički veznik (implikacija), a ne dva, kao u zakonu isključenja trećeg (disjunkcija i negacija), pa će priča iz tog razloga biti jednostavnija. Lično smatram da nije bitno koje oznake koristimo, nego sadržaj tvrđenja o kome govorimo. Možda je ipak bolje da se vratimo na Pirsov zakon, pošto u njemu figuriše samo jedan logički veznik (implikacija), a ne dva, kao u zakonu isključenja trećeg (disjunkcija i negacija), pa će priča iz tog razloga biti jednostavnija.Binarni logički veznik mogu da označim i simbolom 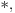 ako hoću. No, da li će ako hoću. No, da li će 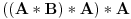 biti Pirsov zakon nezavisno od toga šta je biti Pirsov zakon nezavisno od toga šta je 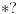 Da li je Da li je 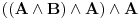 Pirsov zakon? Ne može se Pirsov zakon? Ne može se  zamenjivati bilo kojim veznikom, pa da se dobijena formula zove Pirsov zakon. Pirsov zakon je zakon na jeziku implikacije (znači, klasične). Ako stavim neki drugi veznik umesto implikacije, to više neće biti Pirsov zakon. zamenjivati bilo kojim veznikom, pa da se dobijena formula zove Pirsov zakon. Pirsov zakon je zakon na jeziku implikacije (znači, klasične). Ako stavim neki drugi veznik umesto implikacije, to više neće biti Pirsov zakon.Citat: uranium: Da je to stvarno tako, ne bi ni bilo razlike između klasične i int. logike - seti se da si i sam više puta rekao da su međusobni odnosi veznika ono što ih određuje. Npr. već pomenutu implikaciju nije moguće definisati u int. logici - i sam si lepo objasnio zašto (ono kako si ti definisao "klasičnu" implikaciju ne mogu da računam iz prethodno pominjanih razloga). Teoremu o definljivosti klasičnih veznika u intuicionizmu nisam ja izmislio. To uopšte nije sporno među logičarima koji se bave intuicionizmom, kao ni da u navedenom aksiomatskom sistemu 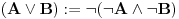 jeste definicija klasične disjunkcije. Intuicionističku disjunkciju nije moguće definisati unutar klasične logike, kao ni intuicionističku implikaciju, kao ni konstruktvnost. To je suštinska razlika između njih. Dakle, razlika postoji. jeste definicija klasične disjunkcije. Intuicionističku disjunkciju nije moguće definisati unutar klasične logike, kao ni intuicionističku implikaciju, kao ni konstruktvnost. To je suštinska razlika između njih. Dakle, razlika postoji. Jedino mi nije jasno gde sam to tvrdio da se klasična implikacija ne može definisati u intuicionističkoj logici. Ja upravo tvrdim suprotno. Citat: uranium: I to na osnovu definicije disjunkcije i jeste teorema ali to ne možeš zvati zakonom isključenja trećeg. A zašto ne mogu? Ako ti smeta to što je disjunkcija izvedeni, a ne polazni veznik, pa je yakon isključenja trećeg u razvijenom obliku zapisan preko konjunkcije i negacije, umesto toga može se skup polaznih veznika proširiti simbolom 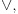 a onda dodati sledeće aksiome: a onda dodati sledeće aksiome: 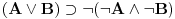 i i 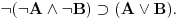 Suština se ne menja. Da li ćeš onda formulu Suština se ne menja. Da li ćeš onda formulu 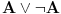 prihvatiti kao zakon isključenja trećeg? Ta formula će svakako biti teorema, a i dalje će sistem obuhvatati koncepte koji nisu definljivi u klasičnoj logici. prihvatiti kao zakon isključenja trećeg? Ta formula će svakako biti teorema, a i dalje će sistem obuhvatati koncepte koji nisu definljivi u klasičnoj logici.Citat: Prvo moramo znati šta je označeno simbolom 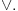 Ako je to konstruktivna disjunkcija, obeležavaću je sa "|". A|B je dokazano ako je bar jedan sastavak dokazan na bar jedan način sredstvima te logike. Recimo, Ako je to konstruktivna disjunkcija, obeležavaću je sa "|". A|B je dokazano ako je bar jedan sastavak dokazan na bar jedan način sredstvima te logike. Recimo, 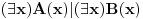 je dokazano ako se dokaže bilo koji od sastavaka je dokazano ako se dokaže bilo koji od sastavaka 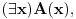 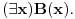 Za razliku od Za razliku od 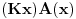 i i 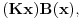 pomenute formule se ne moraju dokazivati konstruktivno. Njihovi indirektni dokazi su takođe obuhvaćeni intuicionističkom logikom. pomenute formule se ne moraju dokazivati konstruktivno. Njihovi indirektni dokazi su takođe obuhvaćeni intuicionističkom logikom.Citat: uranium: Pogledaj šta si svojevremeno napisao. Vidim, ali ne mislim da to protivreči ovome što ovde pišem. Naprotiv, tamo sam istakao razliku između zadataka tipa "dokazati da postoji objekat takav da ..." i "naći objekat takav da...". To su različite stvari i za njih imamo odvojene kvantifikatore 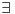 i i 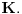 Oba su obuhvaćena intuicionističkom logikom. Jedan zahteva nalaženje svedoka, a drugi ne. Oba su obuhvaćena intuicionističkom logikom. Jedan zahteva nalaženje svedoka, a drugi ne.Citat: uranium: Je l' ja sad treba da kažem da ova tvoja rečenica nije teorema? Pojam "smisao" zaista nije matematički, pa moja rečenica u kojoj se on pojavljuje nije matematički iskaz, pa ne može biti ni teorema. Međutim, kada sam pisao o tome, radilo se o nečemu drugom. U matematičkoj logici postoji potreba za poređenjem logika. Naravno, matematičkim putem, pa se jednakost logika ne može definisati preko "smisla" tih logika ili drugih nematematičkih pojmova. Citat: uranium: Uopšte ne razumem zašto pominješ Pirsov zakon kada ni on ne važi Pirsov zakon pominjem kao 1. Ravnopravnu zamenu za zakon isključenja trećeg u aksiomatizaciji klasične logike koju sam naveo. 2. Zakon u kome figuriše samo jedan logički veznik (implikacija) umesto dva, kao u zakonu isključenja trećeg (disjunkcija i negacija), pa se izlaganje malo pojednostavljuje. Za njega mislim da važi u istom smislu u kome važi i zakon isključenja trećeg. Citat: uranium: opet naglašavam da tvoju definiciju implikacije ne mogu da prihvatim za klasičnu ili ako više voliš - ono što si ti napravio ne mogu da prihvatim za intuicionističku logiku). A ja naglašavam da se za sve navedene logičke rezultate znalo pre nego što samse ja rodio. Tu nema mojih definicija. No, svejedno. Ovo znači da se ne slažeš sa onim što je opšteprihvaćeno u logici. No, to nije ništa loše. Kao da sam ja pa nešto bolji. Na osnovu definicije poređenja logika i veznika, ono jeste aksiomatizacija intuicionističke logike sa sistemom veznika 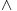 za konjunkciju, za konjunkciju,  za intuicionističku disjunkciju, za intuicionističku disjunkciju,  za negaciju, za negaciju, 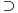 za intuicionističku implikaciju; operatorima za intuicionističku implikaciju; operatorima 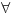 za univerzalnu kvantifikaciju, za univerzalnu kvantifikaciju,  za konstruktivno postojanje i simbolom za konstruktivno postojanje i simbolom  za jednakost. Bar tako misle logičari koji su se bavili intuicionizmom. Takođe, zna se i da (klasična) disjunkcija, (klasična) implikacija i kvantifikator (klasičnog) postojanja jesu definljivi u toj logici, kao i da su ono njihove moguće definicije. To nije sporno među logičarima. Evo, šta može biti sporno: za jednakost. Bar tako misle logičari koji su se bavili intuicionizmom. Takođe, zna se i da (klasična) disjunkcija, (klasična) implikacija i kvantifikator (klasičnog) postojanja jesu definljivi u toj logici, kao i da su ono njihove moguće definicije. To nije sporno među logičarima. Evo, šta može biti sporno:Sami za sebe, simboli 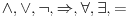 uvedeni onim sistemom jesu simboli klasične logike u odgovarajućim značenjima (da ih ne nabrajam). Isto tako, simboli uvedeni onim sistemom jesu simboli klasične logike u odgovarajućim značenjima (da ih ne nabrajam). Isto tako, simboli 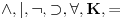 uvedeni onim sistemom jesu simboli intuicionističke logike u odgovarajućim značenjima (da ih ne nabrajam). Međutim, da li se to može tvrditi za oba ta sistema u ukupnosti? Drugim rečima, da li je moguće uvesti neki neekvivalentan sistem (sa simbolima uvedeni onim sistemom jesu simboli intuicionističke logike u odgovarajućim značenjima (da ih ne nabrajam). Međutim, da li se to može tvrditi za oba ta sistema u ukupnosti? Drugim rečima, da li je moguće uvesti neki neekvivalentan sistem (sa simbolima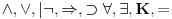 ) čija bi restrikcija na simbole ) čija bi restrikcija na simbole 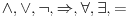 bila klasična logika, bila klasična logika, a restrikcija na simbole 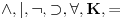 intuicionistička logika. intuicionistička logika.Odgovor na poslednje pitanuje je pozitivan. Zbog toga se klasična logika ne definiše unutar intuicionističke. Kako izdvojiti jedan privilegovan način potapanja. Na koji način tvrditi da je to potapanje "bolje" od nekog drugog (neekvivalentnog). Nije u svim potapanjima klasične logike u intuicionističku 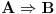 intuicionistički ekvivalentno sa intuicionistički ekvivalentno sa 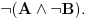 Ja se ne slažem oko formulacije zakona isključenja trećeg itd. Obzirom na poslednju napomenu, tvoja primedba da zapravo nije jasno šta je zakon isključenja trećeg u intuicionizmu, je sasvim na mestu. Zahvaljujući tome što se sistem simbola 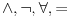 ne razlikuje u klasičnoj i intuicionističkoj logici, a čini bazu klasične logike, to sam koristio za potapanje. Međutim, meni je time garantovana samo klasična ekvivalencija između na primer ne razlikuje u klasičnoj i intuicionističkoj logici, a čini bazu klasične logike, to sam koristio za potapanje. Međutim, meni je time garantovana samo klasična ekvivalencija između na primer 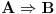 i i 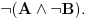 Međutim, klasičnu implikaciju nisam mogao da definišem preko klasične ekvivalencije koja se definiše preko klasične implikacije (circulus viciosus). Međutim, klasičnu implikaciju nisam mogao da definišem preko klasične ekvivalencije koja se definiše preko klasične implikacije (circulus viciosus).[ Nedeljko @ 31.03.2006. 00:00 ] @
Još samo malo da pojasnim nejedinstvenost obuhvatanja klasične i intuicionističke logike u jednu logiku.
Pretpostavimo da imamo sistem sa logičkim simbolima 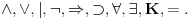 Taj sistem reprodukuje klasičnu logiku ako mu je restrikcija na sistem sa simbolima 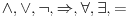 klasična logika u smislu da je formula na tom jeziku teorema tog sistema ako i samo ako je teorema klasične logike. Isto tako, taj sistem reprodukuje intuicionističku logiku ako je njegova restrikcija na sistem sa simbolima klasična logika u smislu da je formula na tom jeziku teorema tog sistema ako i samo ako je teorema klasične logike. Isto tako, taj sistem reprodukuje intuicionističku logiku ako je njegova restrikcija na sistem sa simbolima 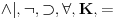 intuicionistička logika u smislu da je formula na tom jeziku teorema tog sistema ako i samo ako je teorema intuicionističke logike. Ako taj sistem u tom smislu reprodukuje obe navedene logike, to nam i dalje ne daje nikakve informacije o međusobnom odnosu klasičnih i intuicionističkih simbola. intuicionistička logika u smislu da je formula na tom jeziku teorema tog sistema ako i samo ako je teorema intuicionističke logike. Ako taj sistem u tom smislu reprodukuje obe navedene logike, to nam i dalje ne daje nikakve informacije o međusobnom odnosu klasičnih i intuicionističkih simbola.Dakle, ako hoćemo obe logike da obuhvatimo jednom, onda znamo koje formule na jeziku klasične logike treba da budu teoreme. To su tačno teoreme klasične logike. Isto tako, znamo koje formule na jeziku intuicionističke logike treba da budu teoreme. To su tačno teoreme intuicionističke logike. Međutim, nije jasno koje od formula koje uključuju i klasične i intuicionističke simbole treba da budu teoreme. Na tom skupu formula se pojavljuje nejedinstvenost. U principu tada između klasičnih i intuicionističkih simbola ne moraju da postoje nikakve međusobne veze. Tada klasična logika neće biti interpretirna unutar intuicionističke. Međutim, čak i ako se ograničimo na definisanje klasičnih simbola preko intuicionističkih, moći ćemo to da uradimo na više neekvivalentnih načina. [ galet@world @ 31.03.2006. 10:29 ] @
Citat: Nedeljko: Ako je a=b, onda se ti uglovi ne mogu oduzimati... Po adicionoj teoremi: cos(α – β) = cos α cos β + sin α sin β. Nigde ne stoji da ova teorema ne važi ako je α = β t.j. nigde nema zabrane da se takvi uglovi ne mogu oduzimati. Ova teorema se bez sumnje odnosi na kosinus kao funkciju uglova. Tvrdnja da se jednaki uglovi ne mogu oduzimati je besmislena, ali se radi o prirodi rezultata tog oduzimanja. Taj rezultat je takav da mu se ne može pridružiti nikakva vrednost funkcije jer u tom slučaju ne postoji argument koji ima dimenziju ugla. [ Nedeljko @ 31.03.2006. 22:22 ] @
Izaberi bilo koji ugao A u ravni. Šta ti je to A-A? Ako taj pojam nije definisan, kako onda možeš govoriti o cos(A-A)? Još bolje, ako su A i B nekekvi uglovi u ravni u opštem položaju, koji ne moraju imati niti jedan zajednički krak, šta je onda A+B ili A-B.
Navedena formula važi bez ikakvih ograničenja za funkciju cos definisanu na skupu realnih (ili kompleksnih) brojeva. Možda je bolje da sa cosr označim kosinusnu funkciju definisanu na skupu realnih brojeva, sa cosk kosinusnu funkciju definisanu na skupu kompleksnih brojeva, a sa cosu kosinusnu funkciju definisanu na skupu uglova u ravni, i slično za sinusne funkcije. Bez ikakvih ograničenja važi sinr(a+b)=sinr(a)cosr(b)+cosr(a)sinr(b), sinr(a-b)=sinr(a)cosr(b)-cosr(a)sinr(b), cosr(a+b)=cosr(a)cosr(b)-sinr(a)sinr(b), cosr(a-b)=cosr(a)cosr(b)+sinr(a)sinr(b), dakle za sve realne vrednosti a i b. Slično tome, bez ikakvih ograničenja važi sink(a+b)=sink(a)cosk(b)+cosk(a)sink(b), sink(a-b)=sink(a)cosk(b)-cosk(a)sink(b), cosk(a+b)=cosk(a)cosk(b)-sink(a)sink(b), cosk(a-b)=cosk(a)cosk(b)+sink(a)sink(b), dakle za sve kompleksne vrednosti a i b. Na uglovima u ravni se takođe definiše funkcija mere, koju ću označiti sa m, koja svakom uglu A pridružuje pozitivan realan broj m(A), pri čemu u slučaju da je zbir uglova A i B definisan, mora da važi m(A+B)=m(A)+m(B) i pri čemu podudarni uglovi moraju imati istu meru. Takva funkcija je određena jednoznačno do na multiplikativnu konstantu. Ako je mera takva da je mera pravog ugla pi/2, onda za ma koji ugao A važe formule sinu(A)=sinr(m(A)), cosu(A)=cosr(m(A)). Dakle, bez ikakvih ograničenja važe formule sinr(m(A)+m(B))=sinu(A)cosu(B)+cosu(A)sinu(B), sinr(m(A)-m(B))=sinu(A)cosu(B)-cosu(A)sinu(B), cosr(m(A)+m(B))=cosu(A)cosu(B)-sinu(A)sinu(B), cosr(m(A)-m(B))=cosu(A)cosu(B)+sinu(A)sinu(B), Često se umesto m(A) piše samo A, i svaka kosinusna funkcija obeležava sa cos, kada nema opasnosti od zabune, ali se uvek mora znati na šta se misli. Ako je u ravni izabran koordinatni koordinatni sistem i razmatraju se samo uglovi kod kojih je jedan krak pozitivan deo x-ose, onda ma koja druga poluprava (znači, ne ta ista) sa temenom u koordinatnom početku određuje tačno dva ugla. Ako se ograničimo samo na one kod kojih je smer od pozitivnog dela x-ose kao kraka ka drugoj osi pozitivan, onda svaka druga poluprava (znači, ne ta ista) sa koordinatnim početkom određuje tačno jedan ugao. Ti uglovi će se meriti realnim brojevima iz otvorenog intervala od 0 do 2pi. Ovakav pojam ugla se može uopštiti tako da svaki realan broj bude mera tačno jednog ugla. No, to neće biti ugao u standardnom geometrijskom smislu, već uređen par čija je prva komponenta poluprava sa temenom u koordinatnom početku, a druga komponenta ceo broj. Dakle, to nije ugao iz geometrije, već sasvim drugi pojam, koji je na neki način povezan sa pojmovima realnog broja i pojmom (geometrisjkog) ugla. Svakom (geometrijskom) uglu odgovara tačno jedan ovakav, pri čemu geometrijskim uglovima odgovaraju uređeni parovi čija je prva komponenta poluprava sa temenom u koordinatnom početku različita od pozitivnog dela x-ose, a druga nula. Na ovakvim uglovima se mogu definisati trigonometrijske funkcije, kojima odgovaraju realne trigonometrijske funkcije. Uglovne trigonometrijske funkcije odgovaraju samo restrikcijama ovih, kao što odgovaraju restrikcijama realnih na interval (0,2pi). Ovakvi uopšteni uglovi se uvek mogu sabirati i oduzimati, a geometrijski uglovi ne. Nije nikakva greška uopštene uglove shvatiti baš kao realne brojeve, a ne parove (poluprava sa centrom u koordinatnom početku, ceo broj), jer postoji prirodna bijekcija između njih (to je upravo funkcija mere uopštenih uglova). Zato nije ni čudo što se mogu uvek sabirati i oduzimati, baš kao realni brojevi. No, geometrijski uglovi su nešto drugo. U matematici se izomorfne strukture po pravilu identifikuju. Zato se niko i ne bavi ovim "uopštenim uglovima", jer je ta struktura izomorfna aditivnoj grupi realnih brojeva. Znači, oni su praktično isto što i realni brojevi. [ uranium @ 01.04.2006. 02:55 ] @
@Nedeljko:
Nadam se da mi nećeš zameriti što malo kasnim sa odgovorom, ali to je bio jedini način da "udahnem duboko i izbrojim do deset". Pošto sam duboko uveren da ovakve rasprave smatraš zabavnim, nemoj se ljutiti ako se i ja malo zabavim u ovom postu. Ni jednog trenutka nisam imao (niti ću imati) nameru da te uvredim. Naravno, taj moj trud ne može nikako biti garancija da te nešto od onoga što budem napisao neće emotivno povrediti, pa se zato unapred (dazanu i) iskreno izvinjavam. Sasvim je moguće da mi je na nekim mestima ton bio preoštar, ali "sintaksno" gledano mislim da sam ostao u granicama pristojnosti (a ako je verovati nekim logičarima iz "sintakse" se da sve videti). U nekima od prethodnih rečenica sam ispustio tonifikator za sarkazam  . .Citat: Nedeljko: Nekako stičem utisak (mada ne mogu da tvrdim, da ne budem pogrešno shvaćen) kao da čitaš samo moje odgovore, a ne i citate koje navodim uz odgovore. Potpuno te razumem, i ja sam se tako osećao dok sam emotivno prilazio ovoj raspravi. Citat: Nedeljko: Zbog toga se klasična logika ne definiše unutar intuicionističke. Eh, da si to na vreme rekao svega ovoga ne bi ni bilo. Toliko si razudio "front" da bih mogao da te citiram do sutra (sve "čestitke" onome ko je napravio sistem za citiranje na ES-u zaista deluje odbijajuće) - ali iz zdravstvenih razloga odustajem od toga (do daljnjeg). Manimo se zato "ćorava posla" i pogledajmo sledeći primer. Neka su date aksiome: 1. 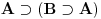 2. 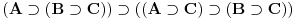 3. 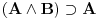 4. 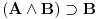 5. 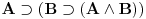 6. 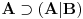 7. 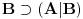 8. 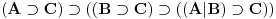 9. 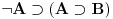 10. 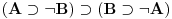 11. 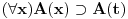 12. 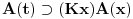 13. 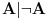 14. 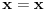 15. 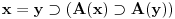 i pravila izvođenja: 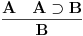 , ,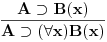 , ,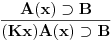 . .Time je određena klasična logika (predikatska sa jednakošću). Ako uklonimo onu nesrećnu aksiomu, dobijamo tvoju intuicionstičku logiku. Ako prihvatimo sve tvoje naknadne definicije (napominjem po ko zna koji put - sintaksno - nemam ništa protiv njih), dobijamo da je klasična logika prava restrikcija sebe same... a znaš gde to vodi. [Ovu poruku je menjao uranium dana 01.04.2006. u 04:00 GMT+1] [ Nedeljko @ 01.04.2006. 11:26 ] @
Citat: uranium: Pošto sam duboko uveren da ovakve rasprave smatraš zabavnim, nemoj se ljutiti ako se i ja malo zabavim u ovom postu. Naravno. Citat: uranium: Ni jednog trenutka nisam imao (niti ću imati) nameru da te uvredim. Ma ne, nisam mislio da si hteo da mene, ili bilo koga drugog povrediš, niti si me na bilo koji način povredio. Samo sam se bojao da sa previše emocija ulaziš u raspravu. No, sve je u redu. Što se tiče razloga zašto se klasična logika ne definiše unutar intuicionsitičke, to su moji zaključci do kojih sam došao naknadno, kroz diskusiju sa tobom. Izgleda da je ova rsprava bila plodna. Citat: uranium: @Nedeljko:dobijamo da je klasična logika prava restrikcija sebe same... a znaš gde to vodi. Ne znam kuda to vodi. Mogao bi to malo da pojasniš. Mnoge strukture imaju izomorfne prave podstrukture, pa šta. Nego, treba razlikovati podračun (to jest račun koji je na istom jeziku, ali ima uži skup teorema, recimo koji se dobija izbacivanjem nekih aksioma) od restrikcije tog računa (to jest računa koji se dobija sužavanjem jezika). Te stvari nisu iste. Veliki pozdrav. [ uranium @ 01.04.2006. 18:27 ] @
Citat: Nedeljko: Ne znam kuda to vodi. Mogao bi to malo da pojasniš. U klasičnoj logici je 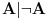 isto što i isto što i 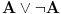 (ovde je veznik (ovde je veznik 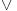 određen kako si ga (standardno) i definisao), pa dobijamo da određen kako si ga (standardno) i definisao), pa dobijamo da 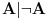 ipak važi i u tvojoj "intuicionističkoj" logici ipak važi i u tvojoj "intuicionističkoj" logici Citat: Nedeljko: Nego, treba razlikovati podračun (to jest račun koji je na istom jeziku, ali ima uži skup teorema, recimo koji se dobija izbacivanjem nekih aksioma) od restrikcije tog računa (to jest računa koji se dobija sužavanjem jezika). Te stvari nisu iste. Hvala na ovom upozorenju (nisam u toku sa standardnom terminologijom, ali očigledno je da si razumeo šta sam hteo da kažem). Veliki pozdrav i tebi [ Nedeljko @ 01.04.2006. 20:17 ] @
Aksiomatski sistem koji si zapisao jeste klasična logika, i tamo
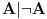 jeste teorema. Ali tu nema ni "i" od intuicionizma. Kada se izbaci aksioma 13, (prelazimo na podračun) onda se dobija intuicionistička logika u kojoj jeste teorema. Ali tu nema ni "i" od intuicionizma. Kada se izbaci aksioma 13, (prelazimo na podračun) onda se dobija intuicionistička logika u kojoj 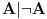 nije teorema. I dalje ne razumem šta je sporno. nije teorema. I dalje ne razumem šta je sporno.Recimo da dodamo još i ove aksiome: 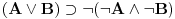 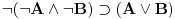 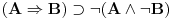 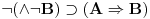 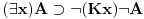 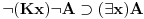 Sa aksiomom 13 imamo klasičnu logiku gde imamo duple oznake za neka značenja. Ukoliko uklonimo aksiomu 13, dobijamo intuicionističku logiku u kojoj te stvari nisu ekvivalentne. Klasična logika će biti restrikcija tog sistema. 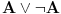 jeste teorema, a jeste teorema, a 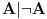 nije. nije.Drugo, to nije moja "intuicionistička", već intuicionistička logika (u varijanti koju sam priložio u pdf fajlu u prvoj poruci), barem po standarnim kriterijumima poređenaj logika. Druga je stvar što ja imam pravo da definišem nove simbole preko polaznih. Na to imam pravo u bilo kom sistemu. [ uranium @ 01.04.2006. 22:17 ] @
Citat: Slažem se. Ja ni ne tvrdim da se koristeći samo takav sistem (bez 13. aksiome) može izvesti 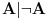 . .Sada definišemo veznik 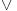 , pa pokažemo da je , pa pokažemo da je 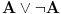 teorema. To je teorema i u nadračunu, šta više, uopšte se ne razlikuje od aksiome teorema. To je teorema i u nadračunu, šta više, uopšte se ne razlikuje od aksiome 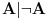 . Time smo pokazali dupliranost oznaka za disjunkciju, pa iako se formalno ne može izvesti . Time smo pokazali dupliranost oznaka za disjunkciju, pa iako se formalno ne može izvesti 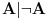 u int. logici, mogli bi reći da i tamo važi (priznajem da to ne bi imalo nikakvo "sintaksno" opravdanje). u int. logici, mogli bi reći da i tamo važi (priznajem da to ne bi imalo nikakvo "sintaksno" opravdanje).Verujem da je uz pomoć nadstrukture pokazano da (držeći se uvedene definicije za disjunkciju) teorema 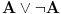 nije zakon isključenja trećeg, jer u protivnom dolazimo do neprijatne situacije, budući da je ono suženje izomorfno nadračunu čije sam aksiome naveo. Kad kažem neprijatna situacija, mislim na sledeće: u int. logici nije izvedivo nije zakon isključenja trećeg, jer u protivnom dolazimo do neprijatne situacije, budući da je ono suženje izomorfno nadračunu čije sam aksiome naveo. Kad kažem neprijatna situacija, mislim na sledeće: u int. logici nije izvedivo 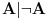 , ali jeste , ali jeste 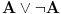 , a te dve teoreme klasične logike su izomorfne slike jedna druge. I kako na kraju reći: "U int. logici je izvediv zakon isključenja trećeg." ili "U int. logici nije izvediv zakon isključenja trećeg." , a te dve teoreme klasične logike su izomorfne slike jedna druge. I kako na kraju reći: "U int. logici je izvediv zakon isključenja trećeg." ili "U int. logici nije izvediv zakon isključenja trećeg."Mislim da bi posle ovoga, zakon isključenja trećeg bio ubijen Sad me baš zanima šta bi se desilo, ako bi nastavili da generišemo nove int. logike u oba smera (u jednom kao raširenje one klasične, a u drugom kao podračun onog suženja); a onda nove klasične u oba smera (u jednom kao nadračun prethodno definisanog int. raširenja, a u drugom kao suženje prethodno definisanog int. podračuna) i tako ad infinitum. Kao što verovatno primećuješ, kada zanemarim semantiku - prinuđen sam da se složim sa dobrim delom tvojih stavova. [Ovu poruku je menjao uranium dana 01.04.2006. u 23:20 GMT+1] [ Nedeljko @ 02.04.2006. 01:29 ] @
Moram priznati da te ne razumem najbolje.
Par veznika 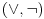 se ne razlikuje od para veznika se ne razlikuje od para veznika 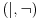 u nadračunu, ali se razlikuje u podračunu upravo zato što u nadračunu, ali se razlikuje u podračunu upravo zato što 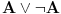 jeste teorema, a jeste teorema, a 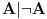 nije teorema. To možeš uporediti sa teorijom pramenova euklidske i apsolutne geometrije. Za paraboličke i hiperboličke pramenove važe iste teoreme u euklidskoj geometriji, ali ne važe iste teoreme u apsoltnoj geometriji. Šta je tu sporno ili neobično? nije teorema. To možeš uporediti sa teorijom pramenova euklidske i apsolutne geometrije. Za paraboličke i hiperboličke pramenove važe iste teoreme u euklidskoj geometriji, ali ne važe iste teoreme u apsoltnoj geometriji. Šta je tu sporno ili neobično?Pretpostavljam da semantiku logike vezuješ za njen smisao. U logici se modeli zovu semantikom, a aksiomatski sistemi sintaksom. Parovi veznika 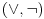 i i 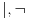 jesu isti (i sintaksno i semantički) u nadračunu, odnosno različiti u podračunu. Razne formule koje su ekvivalentne u ZFC, ne moraju biti ekvialentne u ZF, pa se pri izbacivanju aksiome izbora mnogi pojmovi cepaju na više podpojmova. Sve je to krajnje uobičajeno u matematici. Uopšte ne razumem poentu tvoje priče. jesu isti (i sintaksno i semantički) u nadračunu, odnosno različiti u podračunu. Razne formule koje su ekvivalentne u ZFC, ne moraju biti ekvialentne u ZF, pa se pri izbacivanju aksiome izbora mnogi pojmovi cepaju na više podpojmova. Sve je to krajnje uobičajeno u matematici. Uopšte ne razumem poentu tvoje priče.Sa druge strane, korist od ovog sistema postoji. Omogućava nam da rešavamo i zadatke tipa "Primerom pokazati da postoji..." bez gubljenja bilo čega od klasične logike. [ uranium @ 02.04.2006. 17:52 ] @
Ja se potpuno slažem sa time što si napisao. Zato sam u prethodnom postu napisao
Citat: uranium: (priznajem da to ne bi imalo nikakvo "sintaksno" opravdanje). Ali, prirodno je zapitati se: pa što sam onda to i pominjao? Pa zato što naša situacija nije sasvim ista kao u primerima koje si dao. Neka je 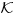 sistem onih aksioma i pravila izvođenja koje sam naveo (neka su u njemu date i one standardne definicije), a neka je sistem onih aksioma i pravila izvođenja koje sam naveo (neka su u njemu date i one standardne definicije), a neka je 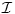 sistem dobijen iz sistem dobijen iz 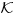 izbacivanjem 13. aksiome, i još neka je izbacivanjem 13. aksiome, i još neka je 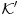 sistem dobijen restrikcijom sistema sistem dobijen restrikcijom sistema 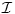 onako kako si opisao u onom materijalu. Ako su onako kako si opisao u onom materijalu. Ako su 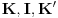 računi koji odgovaraju pomenutim sistemima, onda je lako videti da je svaka teorema intuicionističke logike, teorema i klasične logike, kao i obrnuto, svaka teorema klasične logike je teorema intuicionističke logike (zbog izomorfnosti računi koji odgovaraju pomenutim sistemima, onda je lako videti da je svaka teorema intuicionističke logike, teorema i klasične logike, kao i obrnuto, svaka teorema klasične logike je teorema intuicionističke logike (zbog izomorfnosti  i i 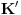 ). ).I šta je to sad? [ Nedeljko @ 02.04.2006. 20:01 ] @
Sistemi K i K' nikako nisu izomorfni, jer sistem K ima širi jezik od sistema K', pa se ne mogu ni porediti. To što su u sistemu K veznici "|" i "v" isti samo znači da taj sistem ima neku vrstu netrivijalnog "automorfizma". Sistem K nema simbol "|" uopšte. Naravno, svejedno je koje ćeš oznake koristiti, ali nije svejedno koliko veznika imaš i koje su arnosti. U tom slučaju je K' prava restrikcija logike I, koja je pravi podračun računa K. Obrati pažnju na razliku između pojmova "restrikcija" i "podračun".
Skup formula sistema K' je pravi podskup skupa formula sistema I koji je jednak skupu formula sistema K. Prihvataš li da postoje teoreme sistema K, pa čak i sistema I, koje nisu formule sistema K'. Jedna od takvih je 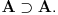 Skup teorema sistema K' je pravi podskup skupa teorema sistema I, koji je pravi podskup skupa teorema sistema K. [ uranium @ 02.04.2006. 20:24 ] @
Citat: Nedeljko: Skup teorema sistema K' je pravi podskup skupa teorema sistema I, koji je pravi podskup skupa teorema sistema K. Slažem se. Ali zar onda imaš pravo da račun 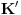 zoveš klasičnom logikom? zoveš klasičnom logikom?Citat: Nedeljko: Sistemi K i K' nikako nisu izomorfni, jer sistem K ima širi jezik od sistema K', pa se ne mogu ni porediti. Ali ako ostavimo definicije onih veznika i onog kvantifikatora tek za račun  zar nećemo onda imati izomorfnost ona dva računa? zar nećemo onda imati izomorfnost ona dva računa?[ Nedeljko @ 03.04.2006. 02:06 ] @
OK, pogrešio sam u prethodnoj poruci. Da se popravim.
Sistem K' jeste tačno klasična logika na jeziku 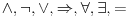 . Ne vidim u tome nikakav problem. Zbog čega ne bi bila? . Ne vidim u tome nikakav problem. Zbog čega ne bi bila?Sistem K takođe jeste tačno klasična na istom jeziku. K i K' su izomorfni. Imaju izomorfne jezike. Sistem I jeste intuicionistička logika na izomorfnom jeziku. Možemo reći da su jezici isti. Recimo da je taj jezik 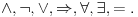 To upravo znači i da je skup formula isti. To upravo znači i da je skup formula isti.Vratimo se sada na tvoje pitanje Citat: Kada potapaš sistem K' u sistem I, ti nećeš svaki polazni logički simbol domena slikati u sebe, već u veznik koji je definljiv u logici koja je kodomen. Time se neće svaka formula domena preslikati u sebe. Recimo, formula 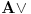 slikaće se u formulu slikaće se u formulu 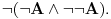 To jeste potapanje, jer se svaak teorema doemna slika u teoremu kodomena. Kada potapaš sistem I u sistem K, ti svaki polazni simbol slikaš u sebe samog, pa se samim tim i svaka formula domena slika u samu sebe. I to je potapanje, jer se svaka teorema domena slika u teoremu kodomena. Sistemi K i K' će biti u potpunosti isti, ali će sistem I imati uži skup teorema (Nemoj ovde da brzaš, pročitaj tekst do kraja, Vreba jedna "optička varka".). Dakle, neće klasična i intuicionistička logika biti iste. To jeste potapanje, jer se svaak teorema doemna slika u teoremu kodomena. Kada potapaš sistem I u sistem K, ti svaki polazni simbol slikaš u sebe samog, pa se samim tim i svaka formula domena slika u samu sebe. I to je potapanje, jer se svaka teorema domena slika u teoremu kodomena. Sistemi K i K' će biti u potpunosti isti, ali će sistem I imati uži skup teorema (Nemoj ovde da brzaš, pročitaj tekst do kraja, Vreba jedna "optička varka".). Dakle, neće klasična i intuicionistička logika biti iste.Seti se samo da se svaki od intervala [0,1), (0,1] može utopiti u onaj drugi, ali da oni nikako nisu izomorfni. Ne kažem da si tvrdio suprotno, niti da to ne znaš, već samo napominjem da to treba stalno imati u vidu. Međutim, isti simbol će u različitim sistemima označavati različite veznike. Zato je bolje da kažemo da sistem I ima jezik 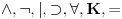 da ne bi bilo opasnosti od "optičke varke" da je u sistemu I formula da ne bi bilo opasnosti od "optičke varke" da je u sistemu I formula 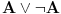 formulacija zakona isključenja trećeg. sistem K se tada utapa u sistem I, mi ćemo u principu polazne simbole iz domena slikati u izvedene simbole kodomena, pa će se formula formulacija zakona isključenja trećeg. sistem K se tada utapa u sistem I, mi ćemo u principu polazne simbole iz domena slikati u izvedene simbole kodomena, pa će se formula 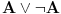 slikati u formulu slikati u formulu 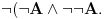 Sa druge strane, pri potapanju sistema I u sistem K ćemo polazne simbole domena slikati u polazne simbole kodomena. Na primer, Sa druge strane, pri potapanju sistema I u sistem K ćemo polazne simbole domena slikati u polazne simbole kodomena. Na primer, 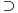 u u 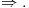 Kada se eliminiše "optička varka", onda više skup teorema sistema I nije inkluzijski uporediv sa skupom teorema sistema K. No, i ovde imamo jednu "optičku varku". Nismo uračunali simbole koji mogu biti definisani preko polaznih. Pretpostavimo da je K'' sistem dobijen proširivanjem sistema K novim sibolima definisanim preko polaznih. Ukoliko upotrebimo barem jedan intuicionistički simbol u tom proširenju, onda zahtevamo da sistem K'' i sistem I na preseku njihovih skupova formula imaju isti skup teorema. Drugim rečima, ne dopuštamo upotrebu istog simbola u različitim značenjima. Tada možeš formirati sistem I' proširivanjem sistema I svim sibolima sistema K'' koji nisu simboli sistema I, definisanim preko polaznih simbola sistema I, tako da skup teorema sistema I' i K'' na skupu formula sistema K'' bude isti, i da skup teorema sistema K'' bude pravi podskup skupa teorema sistema I'. U obrnutom smeru se to ne može uraditi. To je zato što se svi klasični simboli mogu definisati unutar intuicionističke logike, ali se svi intuicionistički ne mogu definisati u okviru klasične logike. Kada definišemo u sistemu I nove simbole preko polaznih, dobićemo sistem čiji je skup teorema pravi nadskup skupa teorema [ uranium @ 03.04.2006. 22:28 ] @
Neka je
 zadat na jeziku zadat na jeziku 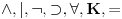 , i neka je , i neka je  zadat na jeziku zadat na jeziku 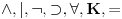 , i neka je , i neka je 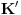 zadat na jeziku zadat na jeziku 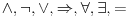 . .Znači, kada iz postojeće klasične logike želim da generišem podračun izomorfan intuicionističkoj logici, meni uopšte nisu potrebni novi simboli - ostavljam isti jezik, ali izbacujem onu aksiomu. Kada iz postojeće intuicionističke logike, pokušavam da napravim račun izomorfan sa klasičnom logikom, onda moram prvo da proširim jezik, pa da ga restrikujem. Uvođenjem novih definicija u sistem  dobijamo bogatiji jezik i njemu odgovarajući sistem dobijamo bogatiji jezik i njemu odgovarajući sistem 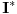 koji je raširenje sistema koji je raširenje sistema  . Dakle, jedino što možemo da tvrdimo je to da intuicionistička logika ima raširenje koje obuhvata klasičnu logiku, a ne da je ona sama raširenje klasične logike. . Dakle, jedino što možemo da tvrdimo je to da intuicionistička logika ima raširenje koje obuhvata klasičnu logiku, a ne da je ona sama raširenje klasične logike.Pomalo je neprijatno i to što sistem 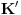 nema pravila izvođenja na sopstvenom jeziku, nego mora da se služi "uslugama" svog raširenja. nema pravila izvođenja na sopstvenom jeziku, nego mora da se služi "uslugama" svog raširenja.[Ovu poruku je menjao uranium dana 03.04.2006. u 23:45 GMT+1] [ Nedeljko @ 03.04.2006. 23:15 ] @
Uvođenjem definicija se u sučtini ne obogaćuje sistem. Utapanje jedne logike u drugu je nekakvo preslikavanje skupa formula logike koja je domen u skup formula logike koja je kodomen, ali da se pritom na ranije opisani način prati struktura formula i da se svaka teorema domena slika u teoremu kodomena.
Postoji utapanje f intuicionističke logike (I) u klasičnu logiku (K) takvi da za ma koju formulu F intuicionističke logike važi F je teorema sistema I => f(F) je teorema sistema K. Sa druge strane, ne postoji takvo utapanje f za koje bi još važilo i F je teorema sistema I <=> f(F) je teorema sistema I za svaku formulu F sistema K. Međutim, postoji utapanje g sistema K u sistem I takvo da za svaku formulu sistema K važi F je teorema sistema K <=> g(F) je teorema sistema I. Drugim rečima, klasična logika je podlogika intuicionističke u jačem smislu od smisla u kome je intuicionistička logika podlogika klasične logike. Ja sam ranije pisao o tome da se (polazni) simboli doemena moraju slikati u (polazne) simbole kodomena. Ne, kod utapanja se (polazni) simboli domena slikauju u simbole koji se mogu definisati u sistemu koji je kodomen. [ uranium @ 04.04.2006. 02:54 ] @
Citat: Nedeljko: Sa druge strane, ne postoji takvo utapanje f za koje bi još važilo i F je teorema sistema I <=> f(F) je teorema sistema I za svaku formulu F sistema K. Pretpostavljam da si hteo: Citat: F je teorema sistema I <=> f(F) je teorema sistema K za svaku formulu F sistema K. Citat: Nedeljko: Uvođenjem definicija se u sučtini ne obogaćuje sistem. Jednim delom se slažem, ali kada se sve teoreme u kojima se javljaju definisani simboli, očiste od tih simbola tj. svedu na polazne simbole - dobijamo nešto što više nije izomorfno klasičnoj logici. Zato, još uvek ostajem pri tvrdnji: Citat: uranium: Dakle, jedino što možemo da tvrdimo je to da intuicionistička logika ima raširenje koje obuhvata klasičnu logiku, a ne da je ona sama raširenje klasične logike. [ Nedeljko @ 04.04.2006. 12:30 ] @
Citat: uranium: Pretpostavljam da si hteo: Da, jeste, upravo sam to hteo da kažem. Citat: uranium: kada se sve teoreme u kojima se javljaju definisani simboli, očiste od tih simbola tj. svedu na polazne simbole - dobijamo nešto što više nije izomorfno klasičnoj logici. Po čemu nije izomorfno. Navedeno utapanje jeste izomorfizam. Dakle, ovako. Ograničimo se radi jednostavnosti na iskazni slučaj. Neka su data dva sistema S i S'. Ako svakom n-arnom vezniku * sistema S pridružimo formulu F*(p1,...,pn), sistema S', a onda definišemo presliakvanje f skupa formula sistema S u skup formula sistema S' na sledeći način: f(p)=p, gde je p proizvoljno iskazno slovo (recimo da su u oba sistema ista), f(*(A1,...,An))=F*(f(A1),...,f(An)), gde je * bilo koji iskazni veznik sistema S, a A1,...,An proizvoljne formule sistema S. Ako pritom za svaku formulu sistema S važi A je teorema sistema S => f(A) je teorema sistema S', onda ćemo reći da je f slabi homomorfizam sistema S u sistem S'. Ukoliko pak za svaku formulu sistema S važi A je teorema sistema S <=> f(A) je teorema sistema S', onda ćemo za f reći da je jaki homomorfizam sistema S u sistem S'. (Jako) utapanje definišemo hao 1-1 (jaki) homomorfizam, a izomorfizam kao jaki bijektivni homomorfizam. Po čemu onda dobijana sistem K' nije izomorfan sistemu K? U euklidsku geometriju i bilo koju drugu matematičku teoriju kada aksiomatizuješ, polazne pojmove možeš izabrati na mnogo načina, a da uvek dobiješ istu teoriju. [ uranium @ 04.04.2006. 14:22 ] @
[ Nedeljko @ 04.04.2006. 22:58 ] @
A zašto pomenuto preslikavanje nije surjektivno? Obrati pažnju na to da kodomen nije sistem, I, već sistem K'. Koja formula sistema K' nije u slici tog preslikavanja?
[ uranium @ 05.04.2006. 02:41 ] @
Verovatno smo se negde usput razišli
Dakle, ja sam pričao o sledećem, ako je sistem 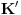 dat na jeziku dat na jeziku 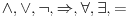 on jeste izomorfan sa sistemom on jeste izomorfan sa sistemom  tu valjda nema ništa sporno. tu valjda nema ništa sporno. Dalje, smatrao sam da su i sistem  i sistem i sistem  dati na jeziku dati na jeziku 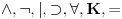 . .Ako se u sistemu 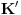 oslobodimo simbola oslobodimo simbola 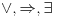 dobijamo formule koje pripadaju sistemu dobijamo formule koje pripadaju sistemu  a time i sistemu a time i sistemu  . Tako da je u tom slučaju reč bila o običnom utapanju prečišćenog sistema . Tako da je u tom slučaju reč bila o običnom utapanju prečišćenog sistema 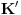 identičkim preslikavanjem iz prečišćenog identičkim preslikavanjem iz prečišćenog 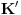 u u  a ne obrnuto. a ne obrnuto.A onda ni jedna formula iz  koja sadrži npr. veznik koja sadrži npr. veznik  ne bi bila slika nijedne formule iz prečišćenog ne bi bila slika nijedne formule iz prečišćenog 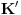 . .Drugim rečima, 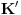 nije suženje sistema nije suženje sistema  , jer njihovi jezici nisu uporedivi u smislu inkluzije. , jer njihovi jezici nisu uporedivi u smislu inkluzije.[ Nedeljko @ 05.04.2006. 10:11 ] @
Prduhitrio si me. Bio sam umoran i zaboravio sam da napomenem da se sve ovo gleda do ne ekvivalenciju.
Formule A i B su u nekom formalnom sistemu ekvivalentne ako je iz hipoteze A izvodivo B i iz hipoteze B izvodivo A. Složićeš se da sada imamo jednu bijekciju između klasa ekvivalencije skupova formula sistema K i K'. [ uranium @ 05.04.2006. 19:14 ] @
Citat: Nedeljko: Složićeš se da sada imamo jednu bijekciju između klasa ekvivalencije skupova formula sistema K i K'. Pre nego što se složim, moram da proverim još nešto. Ako već sve gledamo do na ekvivalenciju, onda umesto izbacivanja aksiome 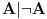 trebalo je da izbacimo čitavu klasu ekvivalencije te aksiome (između ostalih u toj klasi se nalazi i formula trebalo je da izbacimo čitavu klasu ekvivalencije te aksiome (između ostalih u toj klasi se nalazi i formula 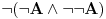 ). Kako bi onda izgledao sistem ). Kako bi onda izgledao sistem  , odnosno sistem , odnosno sistem 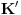 ? Da li bi u njima formula ? Da li bi u njima formula 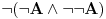 bila teorema? bila teorema? Drugim rečima, ako sve gledamo do na ekvivalenciju, onda se i polazni sistem  može svesti samo na simbole može svesti samo na simbole 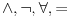 , pa kako onda iz njega izbaciti zakon isključenja trećeg? , pa kako onda iz njega izbaciti zakon isključenja trećeg?[Ovu poruku je menjao uranium dana 05.04.2006. u 20:24 GMT+1] [ Nedeljko @ 06.04.2006. 11:27 ] @
Moram da priznam, da si veoma konstruktivno kritičan.
Teorije (npr. logike) se ne razlikuju po formalnim sistemima koji ih predstavljaju, već po teoremama koje važe u njima. Formule sistema K' su tačno formule na jeziku 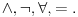 Teoreme sistema I koje su na jeziku sistema K' su tačno logičke istine klasične logike. To je definicija podsistema K'. Nasleđuje se deo formula, kao i one teoreme koje su među tim formulama. Formule sistema K su tačno formule na jeziku Teoreme sistema I koje su na jeziku sistema K' su tačno logičke istine klasične logike. To je definicija podsistema K'. Nasleđuje se deo formula, kao i one teoreme koje su među tim formulama. Formule sistema K su tačno formule na jeziku 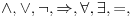 a teoreme su mu tačno formule na tom jeziku koje su logičke istine klasične logike. a teoreme su mu tačno formule na tom jeziku koje su logičke istine klasične logike.No, mi smo krenuli od utapanja sistema K u sistem I. Držimo se toga. [ uranium @ 07.04.2006. 02:06 ] @
Ok, onda smo završili (mrzi me da kopam po literaturi, tako da ću ti verovati na reč da se izomorfnost logika sme svesti na izomorfnost klasa ekvivalencije njihovih teorema bez nekih teških posledica
Zanimljivo je (mada je pomalo offtopic) to da uvođenje/izbacivanje definisanih pojmova unutar teorije i nije baš toliko naivno koliko se možda čini. Tako da, što se mene tiče - to baca senku sumnje na izomorfnost sistema  i i 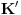 u smislu da ako su zaista izomorfni (preciznije: ako smemo poistovetiti izomorfne sisteme u smislu koji si opisao) - trebalo bi da je moguće - bez proširivanja jezika - iz sistema u smislu da ako su zaista izomorfni (preciznije: ako smemo poistovetiti izomorfne sisteme u smislu koji si opisao) - trebalo bi da je moguće - bez proširivanja jezika - iz sistema 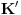 generisati neku intuicionističku logiku - ali to mi deluje skoro nemoguće u našem slučaju... izgleda da ne možemo tvrditi i generisati neku intuicionističku logiku - ali to mi deluje skoro nemoguće u našem slučaju... izgleda da ne možemo tvrditi i Citat: Nedeljko: Teorije (npr. logike) se ne razlikuju po formalnim sistemima koji ih predstavljaju, već po teoremama koje važe u njima. i Citat: Nedeljko: ... da se sve ovo gleda do na ekvivalenciju. Naravno, ovo je samo lični utisak... [Ovu poruku je menjao uranium dana 07.04.2006. u 03:53 GMT+1] [ Nedeljko @ 07.04.2006. 11:30 ] @
@uranium
Ja sse ne sećam da sam se na forumu za matematiku tako nalupetao kao sada u diskusiji sa tobom. To je zato što govorim o ojmovima o kojima sam jako davno slušao na logičkom seminaru. No, nije bitno. U knjizi "Matematička logika - klasična teorija sudova" Vladimira Devidea dato je nekoliko aksiomatskih sistema za klasičnu iskaznu logiku na različitim jezicima. Svi ti sistemi, mada imaju različite alfabete, predstavljaju opis iste, klasične iskazne logike. Treba videti da li je klasična logika podlogika intuicionističke u istom smislu u kome su svo oni sistemi iz Devideove knjige različiti opisi iste logike. Citat: Zeleni Obad: Svasta... pa sta li bi to moglo biti tako komplilkovano? ;) Ljudi mozda, ili - sam razum? :) Ne radi se o komplikovanosti, već o ograničenjima samog naučnog metoda. Pogledaj kojim se pitanjima uopšte bavi filozofija. Kako bi naučni metod mogao da odgovori na pitanja morala (etika), na primer? [ uranium @ 07.04.2006. 14:49 ] @
@Nedeljko:
Meni ostaje još samo da ti se zahvalim na ogromnom strpljenju i na obilju novih informacija koje si mi pružio - malo je reći da moj pogled na ovu temu nije ni izbliza onakav kakav je bio pre nedelju dana To što smo obojica više puta promenili mišljenje o istoj stvari - pripisujem osveti dijalektičke logike [ Nedeljko @ 07.04.2006. 16:34 ] @
Ama, nema šta da mi se zahvaljuješ. I meni su tvoje konstruktivne (da ne kažem intuicionističke ;-) malo [ale nije na odmet) kritike pomogle da se prisetim nekih stvari, i da neke stvari raščistim. Ovaj forum valjda i služi za to.
[ qzqzqz @ 25.04.2006. 14:47 ] @
Na kojoj teoriji se zasniva savremena matematika? Do pre nekoliko decenija to je bila Kantorova teroija skupova, ali su tu pronalizili neke bagove.
[ Nedeljko @ 26.04.2006. 10:58 ] @
Od zasnivanja na Kantorovoj teoriji skupova je prošlo mnogo više od nekoliko decenija. Danas se matematika yasniva na aksiomatskoj teoriji skupova. Najrasprostranjeniji sistem aksioma teorije skupova je ZFC (Cermelo Frankelova sistem).
[ qzqzqz @ 26.05.2006. 20:34 ] @
Koliko je matematika primenljiva u realnom zivotu, sa obzirom na razlicitost aksioma teorija?
[ Nedeljko @ 28.05.2006. 22:10 ] @
Matematika tvrdi da u svakom modelu svake matematičke teorije (znači, pri svakoj interpretaciji polaznih pojmova te teorije pri kojoj važe sve njene aksiome) važe sve teoreme te matematičke teorije.
Kada primenjuješ matematiku, ti koristiš neku konkretnu interpretaciju polaznih pojmova neke matematičke teorije. Matematika ne tvrdi da će u toj interpretaciji obavezno važiti aksiome te teorije, već da ako one važe, onda da moraju da važe i sve teoreme te teorije. Provera da li aksiome te teorije važe u toj interpretaciji ostaje na tebi. Ukoliko tu matematičku teoriju primenjuješ van matematike, onda ta interpretacija nije matematička jer povezuje matematičke i nematematičke pojmove, pa se ta provera ne može vršiti matematičkim sredstvima. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|