[ Lobacev @ 29.03.2006. 12:13 ] @
| Neka je i=sqr(-1). 1. i=i 2. sqr(-1)=sqr(-1)=sqr(-1/1)=sqr(1/-1)=sqr(1)/sqr(-1) 3. sqr(-1)*sqr(-1)=sqr(1) 4. -1=1 Gde je greška? |
|
[ Lobacev @ 29.03.2006. 12:13 ] @
[ del-boy @ 29.03.2006. 12:51 ] @
Koren iz -1 nije samo i nego i -i! Kompleksni koren...
Koliko se sećam na ESu je bilo par tema na ovaj fazon da se preko i dolazi do izraza 1=-1! [Ovu poruku je menjao del-boy dana 29.03.2006. u 13:52 GMT+1] [ Daniel011 @ 30.03.2006. 09:14 ] @
Zanimljiv štos, jedino mi nikako nije jasno kako si iz 3. koraka stigao do 4.?
Razumeo sam sve do 3. koraka, ali iz 3. uopšte ne uspevam da vidim zašto bi -1 trebalo da bude jednako 1? [ Lobacev @ 30.03.2006. 10:19 ] @
Objašnjenje za 3. korak:
3.a. sqr(-1)*sqr(-1)=1 3.b. i*i=1 3.c. -1=1 [ Milan Gligorijevic @ 30.03.2006. 10:57 ] @
[ Lobacev @ 30.03.2006. 11:13 ] @
Da li to znači da ne važi sledeća jednakost:
sqr(a/b)=sqr(a)/sqr(b) ? ili da ne važi (-a)/b=a/(-b)? [ Daniel011 @ 30.03.2006. 11:13 ] @
Citat: Lobacev: Objašnjenje za 3. korak: 3.a. sqr(-1)*sqr(-1)=1 3.b. i*i=1 3.c. -1=1 Tačno, očigledno je, ali mi je nekako promaklo. Inače slažem se sa onim što kaže del-boy da  može biti i može biti i  i i  . .Citat: mmwc: ovo nije jednako "sqr(1/-1)=sqr(1)/sqr(-1)" Očigledno je da nije jednako, ali u čemu je greška u tom izrazu? Koren količnika dva broja valjda jeste jednak količniku korena ta dva broja. [ Milan Gligorijevic @ 30.03.2006. 11:21 ] @
uzmi papir i olovku i probaj
sqr(1)/sqr(-1) pomnozi sa sqr(-1)/sqr(-1) i dobijes iznad razlomacke crte sqr(-1) sto je jednako i, a ispod razlomacke crte sqr(-1)*sqr(-1) sto je jednako -1 pa je rezultat celog razlomka -i [ Daniel011 @ 30.03.2006. 11:39 ] @
Citat: mmwc: uzmi papir i olovku i probaj sqr(1)/sqr(-1) pomnozi sa sqr(-1)/sqr(-1) i dobijes iznad razlomacke crte sqr(-1) sto je jednako i, a ispod razlomacke crte sqr(-1)*sqr(-1) sto je jednako -1 pa je rezultat celog razlomka -i To definitivno nije sporno, ali ja samo pitam u čemu je greška ako se napiše da je 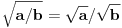 ? ?[ Bojan Basic @ 30.03.2006. 12:31 ] @
[ Lobacev @ 30.03.2006. 14:24 ] @
Matematika nije TABU nauka pa da nešto zabranjuje. Može se reći da nešto MOŽE da se uradi (i zašto može) ili NE MOŽE da se uradi (i zašto ne može). A sada jedno malo pitanje čije rešenje će nas približiti odgonetki:
U izrazu y=sqrt(x**2) (kvadratni koren od x na kvadrat) koji je redosled operacija: da li se prvo radi kvadriranje pa korenovanje, korenovanje pa kvadriranje ili je to svejedno? [ Daniel011 @ 30.03.2006. 15:32 ] @
Citat: Lobacev: U izrazu y=sqrt(x**2) (kvadratni koren od x na kvadrat) koji je redosled operacija: da li se prvo radi kvadriranje pa korenovanje, korenovanje pa kvadriranje ili je to svejedno? Logičnije je da se u ovom konkretnom slučaju prvo radi kvadriranje, s obzirom da je ovde kvadriranje navedeno u okviru argumenta funkcije korenovanja. Nego, ja sam upravo dokazao da je 1=0 ! :-) (Molim vas da ovo shvatite isključivo kao šalu i nikako drugačije): Pošto je 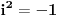 , sledi , sledi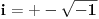 Sada nađemo 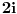 : :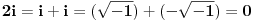 (Prvo  u gornjem izrazu je zamenjeno izrazom u gornjem izrazu je zamenjeno izrazom 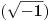 , a drugo izrazom , a drugo izrazom 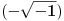 , jer , jer  , kao što smo rekli, može biti i jedno i drugo.) , kao što smo rekli, može biti i jedno i drugo.)Iz ovoga sledi da je 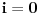 ! !Samim tim je i 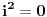 , a pošto je po definiciji , a pošto je po definiciji 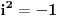 , odatle je , odatle je 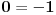 . Ako obe strane jednačine pomnožimo sa . Ako obe strane jednačine pomnožimo sa  , dobijemo , dobijemo 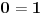 ! ![ Farenhajt @ 30.03.2006. 20:11 ] @
Pa dakle, Bojan je (ispravno) tvrdio da nije tačno
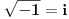 nego da se mora reći nego da se mora reći 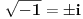 . .U tome je i suština greške u Lobačevljevom početnom postu: Naime, u izrazu 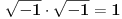 PREĆUTNO je uzeto da jedan kvadratni koren ima vrednost PREĆUTNO je uzeto da jedan kvadratni koren ima vrednost  , a drugi , a drugi 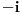 . Naravno, to je logički moguće (ne postoji zakon protiv međusobnog množenja svih različitih vrednosti određenog korena), ali, međutim, ne odgovara definiciji kvadriranja, gde se jedna te ISTA vrednost mora množiti sama sa sobom. . Naravno, to je logički moguće (ne postoji zakon protiv međusobnog množenja svih različitih vrednosti određenog korena), ali, međutim, ne odgovara definiciji kvadriranja, gde se jedna te ISTA vrednost mora množiti sama sa sobom.Takođe, u malopređašnjem postu, operacija "množenje određene vrednost brojem 2" po definiciji je ekvivalentna dodavanju te iste vrednosti samoj sebi, te se - naravno! - ne može pisati 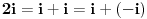 (Greška je, dakle, slična ovome: 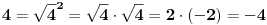 ) )[Ovu poruku je menjao Farenhajt dana 30.03.2006. u 21:17 GMT+1] [ Lobacev @ 31.03.2006. 07:20 ] @
Nije baš sasvim tako kako kaže Farenhajt, ali LIČI! Problem je što se u koraku
sqr(-1/1)=sqr(1/-1) prećutno uzima da je sqr(-1)*sqr(-1)=1, a u poslednjem koraku se uzima da je sqr(-1)*sqr(-1)=-1. Oba tvrđenja su tačna, ali se ne mogu uzimati različita rešenja u isto vreme, npr. kao što iz 1=1 sledi da je sqr(1)=sqr(1) +-1=+-1 ali se odavde ne može tvrditi da je +1=-1 napomena: sqr(-1/1)=sqr(-1)/sqr(1)= (sqr(-1)/sqr(1))*(sqr(-1)/sqr(-1))= =sqr(-1)*sqr(-1)/(sqr(1)*sqr(-1))= sqr(-1)*sqr(-1)/sqr(-1) vrednost izraza sqr(-1)*sqr(-1) mora biti konzistentna tokom čitavog procesa rešenja problema, t.j. uzima se ILI vrednost 1 ILI -1. [Ovu poruku je menjao Lobacev dana 31.03.2006. u 08:25 GMT+1] [ Nedeljko @ 01.04.2006. 19:02 ] @
To je zato što se samo mućka sa izrazima, a da se ne zna šta zapravo znači šta.
Postoje različiti kvadratni koreni u matematici. Analitički koren je funkcija koja slika nenegativne realne brojeve u nenegativne realne brojeve. Za nenegativne realne brojeve 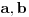 važi važi 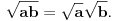 Algebarski koren iz nekog kompleksnog broja je bilo kouji kompleksan broj čiji je kvadrat upravo taj dati broj. Postoje tačno dva kvadratna korena iz bilo kog kompleksnog broja različitog od nule. Tu se ne može primenjivati pomenuta formula. Slično važi i kod kompleksnog kvadratnog korena, bez obzira da li se radi na dvolisnoj površi ili na jednostruko povezanoj oblasti kojoj ne pripada nula. Bojan je u pravu kada kaže da izraz Algebarski koren iz nekog kompleksnog broja je bilo kouji kompleksan broj čiji je kvadrat upravo taj dati broj. Postoje tačno dva kvadratna korena iz bilo kog kompleksnog broja različitog od nule. Tu se ne može primenjivati pomenuta formula. Slično važi i kod kompleksnog kvadratnog korena, bez obzira da li se radi na dvolisnoj površi ili na jednostruko povezanoj oblasti kojoj ne pripada nula. Bojan je u pravu kada kaže da izraz 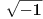 nema previše smisla, a ako se kompleksni koren korektno uvede (na dvolisnoj površi ili jednostruko povezanoj oblasti koja isključuje nulu), onda neće važiti isti algebarski zakoni bez ograničenja. nema previše smisla, a ako se kompleksni koren korektno uvede (na dvolisnoj površi ili jednostruko povezanoj oblasti koja isključuje nulu), onda neće važiti isti algebarski zakoni bez ograničenja.[ mickey6252 @ 02.04.2006. 02:43 ] @
Citat: Lobacev: Matematika nije TABU nauka pa da nešto zabranjuje. Može se reći da nešto MOŽE da se uradi (i zašto može) ili NE MOŽE da se uradi (i zašto ne može) Dakle, ako ti neko, u okviru neke teorije, kaže da nešto ne smeš da uradiš, a zatim ti to i dokaže (kaže ti zašto ne smeš to da uradiš), onda ti je faktički zabranio da to uradiš. To i dalje ne znači da je matematika tabu nauka. Naprotiv, baš zbog toga je matematika vrlo otvorena prema različitim mišljenjima. Ako nešto tvrdiš, pa uz put to i dokažeš... daleko ćeš dogurati. [ Fitopatolog @ 30.04.2006. 20:38 ] @
Sasvim jednostavno i korektno objašnjenje, bez korišćenja "teške artiljerije".
[ galet@world @ 21.07.2006. 09:34 ] @
Sledi, po Bojanu, da se i ne može pisati u drugom obliku nego samo tako t. j. kao simbol. U drugom obliku se može pisati samo i2 t. j.: - 1
[ Fitopatolog @ 30.12.2007. 11:44 ] @
Lepa tema, pa da se malo podsetimo...
[ Boba90 @ 01.01.2008. 19:08 ] @
operacija korenovanja je definisana samo za >= 0 te je zabranjeno napisati da je i koren iz -1 , ali je -1= i na kvadrat tacno...
[ Fitopatolog @ 28.03.2009. 12:26 ] @
Citat: Boba90: operacija korenovanja je definisana samo za >= 0 !? U ovom primeru nemamo takvo ograničenje! [ holononi @ 16.05.2009. 16:33 ] @
1/i = z
1 = iz 1 = (1, 0); i = (0, 1); z = (x, y) (1, 0) = (0, 1)(x, y) (1, 0) = (0*x - 1*y, 0*y + 1*x) (1, 0) = (-y, x) y = -1; x = 0 z = (0, -1) = -(0, 1) = -i = 1/i ------------------------------- z = r*e^(iα) 1/z = (1/r)*1/e^(iα) = (1/r)*e^(-iα) = (1/r)( cos(-α) + i*sin(-α) ) = (1/r)( cosα - i*sinα ) z = i => r = 1, α = π/2 1/i = 1( cos(π/2) - i*sin(π/2) ) = -i [ Nedeljko @ 17.05.2009. 13:19 ] @
Aman ljudi, realan koren nije definisan u tački -1, a za kompleksan koren ne važi
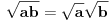 . Definišite korenu funkciju sa kojom radite, pa probajte da proterate izvođenje sa njom. Ako ne razumete matematiku, a zanima vas, to je rešiv prolem. Ne, ovde nije cilj to, već namerno pravljenje mistike niodčega. . Definišite korenu funkciju sa kojom radite, pa probajte da proterate izvođenje sa njom. Ako ne razumete matematiku, a zanima vas, to je rešiv prolem. Ne, ovde nije cilj to, već namerno pravljenje mistike niodčega.Ovaj primer je svakako koristan da bi se videlo da baratanje matematikom bez razumevanja proizvodi besmislene rezultate. [ holononi @ 17.05.2009. 14:29 ] @
Citat: Aman ljudi, U čemu je problem? Ako je to reakcija na moj post onda sam zbunjen jer sam uveo pojam kompleksnog broja kao uredjen par, što je po mom mišljenju jedino ispravno. Sve što je potrebno je jasno definisano i nema zabune sa korenom jer √(-1) je priča za malu decu. Polje kompleksnih brojva se mora posmatrati u ravni da bi se stekla pravilna slika o rezultatima operacija nad kompleksnim brojevima. S druge strane polarno-eksponencijalna forma ekvivalentno definiše kompleksan broj u ravni. [ Nedeljko @ 17.05.2009. 15:30 ] @
Izvinjavam se, nisam ni čitao tvoj post, već sam samo primetio da se još raspravlja o nečemu što je razjašnjeno. Lepo sam napisao šta treba da definiše onaj ko pretenduje na ovakvo izvođenje kontradikcije. Mislim da kompleksni brojevi nisu problem, već korena funkcija.
Zapravo, pročitao sam ovo Citat: Što se tiče tvog posta holononi, nije mi baš jasno šta je poenta. [ Fitopatolog @ 17.05.2009. 18:36 ] @
Zašto je ZABRANJENO? Nisam navikao u matematici na zabrane već na objašnjenja.
Npr. SQR(-1) ima dva rešenja, i i(veznik) -i. Zašto je onda zabranjeno pisati SQR(-1)? !? [ holononi @ 17.05.2009. 19:31 ] @
Citat: Zašto je onda zabranjeno pisati SQR(-1)? Nije zabranjeno. Samo treba biti pažljiv pri korišćenju. Ako je SQR(.) operacija na skupu realnih brojeva tada SQR(-1) nije definisano. Medjutim ako neko hoće da kaže i = SQR(-1) tada mora biti jako oprezan. Kako sam već naveo ispravno je i = (0, 1). Tada se ne dolazi do netačnih tvrdjenja -1=1, 2i=0 i slično. Zašto do toga dolazi. Iz prostog razloga što "račundžija" "šeta" iz jednog polja u drugo. Kad mu odgovara koristi polje realnih brojeva i onda mirne savesti "ušeta" u polje kompleksnih brojeva pa tada dolazi do "čudnih slučajeva". Da se podsetimo, (R, +, *) je polje realnih brojeva sa operacijma sabiranja i množenja kako smo inače navikli još iz osnovne škole. Medjutim struktura (R2, +C, *C) je polje kompleksnih brojeva gde su operacije sabiranja i množenja definisane na sledeći način (a, b) +C (c, d) = (a+c, b+d) (a, b) *C (c, d) = (ac - bd, ad + bc) dok je nula data sa (0, 0), jedinica je (1, 0) a imaginarna jedinica i = (0, 1). Ako se još podsetimo da je -(a, b) = (-a, -b) dobili smo suprotni a može se definisati i inverzni element. U ovako definisanom polju kompleksnih brojeva nema zabune i ništa čudno sa korenom iz minus jedan. √(-1) = z = r*eiΦ -1 = r²e2iΦ -1 = r²( cos(2Φ) + i*sin(2Φ) ) -1 = r²( cos(2Φ) + i*sin(2Φ) ) cos(π) = r²( cos(2Φ) + i*sin(2Φ) ) z1 = z2 <=> Re(z1) = Re(z2) i Im(z1)= Im(z2) r=1 cos(π) = cos(2Φ) => π = 2Φ => Φ = π/2 0 = sin(2Φ) => 2Φ = π ili 2Φ = 0, odnosno Φ = π/2 ili Φ = 0 Φ nemože biti jednako nula jer tada ne bi važilo cos(π) = cos(2Φ), prema tome Φ = π/2. Dakle √(-1) = eiπ/2 = i [ Farenhajt @ 17.05.2009. 20:34 ] @
Citat: Fitopatolog: Zašto je ZABRANJENO? Nisam navikao u matematici na zabrane već na objašnjenja. Npr. SQR(-1) ima dva rešenja, i i(veznik) -i. Zašto je onda zabranjeno pisati SQR(-1)? !? Kao što reče holononi, nije zabranjeno. Ali evo u čemu je kvaka. U skupu realnih brojeva, 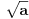 je DOGOVORNO USVOJENA OZNAKA ZA POZITIVNU VREDNOST KORENA. Takav dogovor se može napraviti, jer zbog uređenja polja realnih brojeva uvek možemo nedvosmisleno odrediti šta je pozitivno, a šta negativno. je DOGOVORNO USVOJENA OZNAKA ZA POZITIVNU VREDNOST KORENA. Takav dogovor se može napraviti, jer zbog uređenja polja realnih brojeva uvek možemo nedvosmisleno odrediti šta je pozitivno, a šta negativno.U skupu kompleksnih brojeva se NE MOŽE NAPRAVITI TAKAV DOGOVOR, jednostavno zato što, kao brojevi u ravni, kompleksni brojevi ne poznaju termine "pozitivno" i "negativno" - tj. nema uređenja. Stoga je 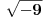 samo KOMPAKTNA OZNAKA ZA SKUP OD DVA KOMPLEKSNA BROJA samo KOMPAKTNA OZNAKA ZA SKUP OD DVA KOMPLEKSNA BROJA 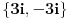 , tj. , tj. 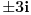 . .E sada, ta "dvogubost" kompleksnog korena mora se imati u vidu čak i ako potkorena veličina "liči" na realan broj, ali ga zapravo tretiraš kao kompleksan - evo šta hoću da kažem: kad napišeš 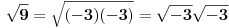 , prvi član u nizu moraš tretirati kao KOMPLEKSAN broj, te ti se jednakost svodi na , prvi član u nizu moraš tretirati kao KOMPLEKSAN broj, te ti se jednakost svodi na 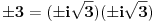 , što je svakako tačno. , što je svakako tačno.Da li ti je sad jasnije? [ Fitopatolog @ 17.05.2009. 20:52 ] @
Citat: Farenhajt: Kao što reče holononi, nije zabranjeno. Ali evo u čemu je kvaka. U skupu realnih brojeva, 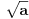 je DOGOVORNO USVOJENA OZNAKA ZA POZITIVNU VREDNOST KORENA. Takav dogovor se može napraviti, jer zbog uređenja polja realnih brojeva uvek možemo nedvosmisleno odrediti šta je pozitivno, a šta negativno. je DOGOVORNO USVOJENA OZNAKA ZA POZITIVNU VREDNOST KORENA. Takav dogovor se može napraviti, jer zbog uređenja polja realnih brojeva uvek možemo nedvosmisleno odrediti šta je pozitivno, a šta negativno.U skupu kompleksnih brojeva se NE MOŽE NAPRAVITI TAKAV DOGOVOR, jednostavno zato što, kao brojevi u ravni, kompleksni brojevi ne poznaju termine "pozitivno" i "negativno" - tj. nema uređenja. Hmmm... Možda ipak možemo napraviti takav dogovor, pošto za bilo koji kompleksan broj z imamo dva korena: sqr(z)= x+iy i takođe sqr(z)= -x-iy= -(x+iy) iz prostog razloga što je drugi koren uvek jednak prvom koji je pomnožen sa e**(i pi) = -1. ? I za realan i za imaginaran deo kompleksnog broja vrlo dobro možemo utvrditi uređenje, pa samim tim imamo uređenje i za kompleksan broj koji oni grade? [ Farenhajt @ 17.05.2009. 22:53 ] @
Citat: Fitopatolog: I za realan i za imaginaran deo kompleksnog broja vrlo dobro možemo utvrditi uređenje, pa samim tim imamo uređenje i za kompleksan broj koji oni grade? Po tom rezonu, kako bi uporedio brojeve 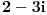 i i 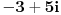 ? I kako bi svaki od njih ponaosob uporedio s kompleksnim brojem ? I kako bi svaki od njih ponaosob uporedio s kompleksnim brojem 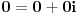 ? ?[ Fitopatolog @ 17.05.2009. 22:58 ] @
Prvi ima veći realni i manji imaginarni deo od drugog.
Analogno ide upoređenje ova dva sa trećim. [ Fitopatolog @ 17.05.2009. 23:01 ] @
Ali mislim da nas to ne sprečava da pišemo
sqr(a)*sqr(b) = sqr(a*b) a i b su kompleksni brojevi. [ Farenhajt @ 17.05.2009. 23:03 ] @
Citat: Fitopatolog: Prvi ima veći realni i manji imaginarni deo od drugog. I kako taj (sasvim tačan) zaključak možeš iskoristiti da ih poređaš u neprestano rastući niz od negativne do pozitivne beskonačnosti, kao što možeš realne brojeve? Ne možeš, pošto kod kompleksnih brojeva imaš "dva stepena slobode", koji te sprečavaju da ih potpuno urediš. MOŽEŠ urediti neke specijalne podskupove skupa kompleksnih brojeva - recimo, brojeve koji (geometrijski) leže na jednoj pravoj, ili na duži, ili na krivoj, ali kompletnu kompleksnu ravan ne možeš urediti. [ Farenhajt @ 17.05.2009. 23:04 ] @
Citat: Fitopatolog: Ali mislim da nas to ne sprečava da pišemo sqr(a)*sqr(b) = sqr(a*b) a i b su kompleksni brojevi. Kao što rekoh, ništa te ne SPREČAVA da to napišeš, ali moraš paziti kako to TUMAČIŠ, a za tumačenje vidi onu moju gornju (dužu) poruku. [ Fitopatolog @ 17.05.2009. 23:06 ] @
Kako bi uporedio dva pravougaonika?
[ Fitopatolog @ 17.05.2009. 23:09 ] @
U čemu je problem ako se napiše sqr(a)*sqr(b) = sqr(a*b)
još uvek ne vidim, daj neki primer? [ Fitopatolog @ 17.05.2009. 23:11 ] @
Citat: Farenhajt: I kako taj (sasvim tačan) zaključak možeš iskoristiti da ih poređaš u neprestano rastući niz od negativne do pozitivne beskonačnosti, kao što možeš realne brojeve? pa već su poređani u ravni koju prave imaginarna i realna osa. Da mogu da se tretiraju kao realni brojevi, kompleksni brojevi nam ne bi ni trebali, zar ne? [ Farenhajt @ 17.05.2009. 23:16 ] @
Citat: Fitopatolog: Kako bi uporedio dva pravougaonika? Sad ću nakratko da privatizujem ovaj forum: Ko boga te molim, nemoj me s pitanjima tipa "kako bi uradio nešto za šta trenutno važeća matematika kaže da se ne može ni definisati, a kamoli uraditi". Još se oporavljam od galet@worldovog slučaja. Citat: Fitopatolog: U čemu je problem ako se napiše sqr(a)*sqr(b) = sqr(a*b) još uvek ne vidim, daj neki primer? Ili ne razumeš srpski jezik, ili se praviš blesav. Dvaput sam rekao da to MOŽE da se piše, ali da NE MOŽE DA SE TUMAČI ONAKO KAKO SE TUMAČI U SKUPU REALNIH BROJEVA, NEGO ONAKO KAKO MORA DA SE TUMAČI U SKUPU KOMPLEKSNIH BROJEVA. Ti to prihvati ili nemoj, tvoja volja, a ja više neću ponavljati. [ Bojan Basic @ 17.05.2009. 23:53 ] @
Citat: Fitopatolog: Prvi ima veći realni i manji imaginarni deo od drugog. Dobro, i recimo da se dva korena nekog kompleksnog broja  odnose baš ovako (jedan ima veći realni a manji imaginarni deo od drugog). Kojeg od njih bi (dogovorno) proglasio za vrednost odnose baš ovako (jedan ima veći realni a manji imaginarni deo od drugog). Kojeg od njih bi (dogovorno) proglasio za vrednost 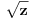 ? ?[ holononi @ 18.05.2009. 00:06 ] @
Da li se dogovaramo oko toga šta je imaginarna jedinica ili pokušavamo da odredimo koliko korena ima kompleksan broj? Može se pisati i = √(-1) dok je -i = -√(-1). Sa druge strane ako je reč o broju korena kompleksnog broja onda ih uvek ima n za n-ti koren, pa tako i za √(-1). Ali te dve vrednosti su različite
z1 = cos(pi/2) + i*sin(pi/2) = i z2 = cos(3pi/2) + i*sin(3pi/2) = -i Iz ovoga ne sledi da su i i -i isto. Niti ima zabune oko definicije. U kompleksnoj ravni će i dalje važiti i = (0, 1) -i = (0, -1) a ovo treba čitati i je zamena za ... a ne shvatati kao jednakost! Samo što je lakše staviti = nego pisati sva ta čuda. To je uopšte problem nastave matematike, gde se direktno prelazi na korišćenje simbola a da nema prethodno jasnog dogovora šta ti simboli znače. Jednom pogrešno stečene navike se posle teško ispravljaju. Pri tome uopšte nisam siguran da li se po tom pitanju može učiniti bilo šta. Nova saznanja nas zatrpavaju kao mećava i predugo zadržavanje oko detalja (koji su važni) ne bi rezultiralo u bilo čemu. Ostaje ono pomalo grubo ali možda jedino realno "ko razume shvatiće". Medjutim, da li smo mogli uzeti i = -√(-1)? Da mogli smo. I čini mi se da se ništa bitno ne bi promenilo. Citat: sqr(a)*sqr(b) = sqr(a*b) Ovo važi samo za realne nenegativne brojeve. Kad su u pitanju kompleksni brojevi, koren je višeznačna funkcija. U polju kompleksnih brojeva nije moguće jednostavno uredjenje (moralo bi da važi a<>b povlači a<b ili a>b). Ako se pretpostavi da takvo uredjenje postoji. Tada i<0 ili i>0 i moralo bi da važi i*i > 0, što je kontradikcija jer je i*i = -1 < 0. [ Fitopatolog @ 18.05.2009. 06:31 ] @
Sve se slažem sa Vama (mada sam ponekad i blesav. Kao što se i Farenhajt ponekad pravi pametan). Da izbegnemo problem sa uređenjam, zadržimo oba korena od sqr(z) ravnopravnim. Za koje oblasti kompleksne ravni tada važi sqr(a)*sqr(b) = sqr(a*b) a za koje ne? [ holononi @ 18.05.2009. 09:37 ] @
√z1 √z2 = w1 w2
w1 = √r1( cos((φ1+2kπ)/2) + isin((φ1+2kπ)/2) ), k=0,1 w2 = √r2( cos((φ2+2mπ)/2) + isin((φ2+2mπ)/2) ), m=0,1 pa u opštem slučaju √z1 √z2 ima 4 rešenja, dok √(z1 z2) = w w = √(r1 r2)( cos((φ1+φ2+2tπ)/2) + isin((φ1+φ2+2tπ)/2) ), t=0,1 u opštem slučaju √(z1 z2) ima 2 rešenja, pa je √z1 √z2 <> √(z1 z2). √z1 √z2 = √(z1 z2) samo ako je φ1 = φ2 = 0, tj. na R+. [ Fitopatolog @ 18.05.2009. 10:19 ] @
Sasvim OK. Ako se ne varam po dva rešenja (od četiri) se uvek poklapaju. Tako da su preostala dva (različita) rešenja jednaka rešenju sqr(a*b).
Mislim da možemo pisati da je sqr(a)*sqr(b) = sqr(a*b) imajući na umu uvek prethodne dve rečenice? da ne bude dileme, imamo w1, -w1, w2 i -w2. w1*w2 se poklapa sa rešenjem (-w1) * (-w2) a (-w1)*w2 se poklapa sa w1*(-w2). [Ovu poruku je menjao Fitopatolog dana 18.05.2009. u 12:03 GMT+1] [Ovu poruku je menjao Fitopatolog dana 19.05.2009. u 21:03 GMT+1] [ Nedeljko @ 20.05.2009. 10:32 ] @
Smem li da pitam o čemu se ovde raspravlja?
[ Fitopatolog @ 20.05.2009. 11:29 ] @
Smeš, zašto ne bi smeo?
[ Nedeljko @ 20.05.2009. 13:45 ] @
[ Cabo @ 20.05.2009. 16:20 ] @
Citat: Nedeljko: I, u čemu je fora? Da li neko misli da je našao 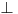 u matematici ili je fabula radnje u nečemu drugom? u matematici ili je fabula radnje u nečemu drugom?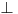 ? „Dno“ ili... ? ? „Dno“ ili... ?[ Nedeljko @ 20.05.2009. 17:20 ] @
Kontradikcija ili dno, u ovom kontekstu se ne razlikuju.
[ holononi @ 28.05.2009. 13:05 ] @
[ braker @ 28.05.2009. 16:46 ] @
Odgovor: e^(i*x) = cosx + i*sinx, za x= pi => e^(i*pi) = -1
[ Fitopatolog @ 17.06.2010. 21:31 ] @
Evo (opet) zgodne teme za rashlađivanje u ovim toplim danima...
[ holononi @ 17.06.2010. 21:57 ] @
Šta bi Euler bez radijana?
eit = cist [ holononi @ 02.03.2011. 14:05 ] @
Č-)
[ holononi @ 03.03.2011. 20:31 ] @
[ holononi @ 04.03.2011. 21:40 ] @
I, šta je zaključak?
da li je ovo Citat: Fitopatolog: Sasvim OK. Ako se ne varam po dva rešenja (od četiri) se uvek poklapaju. Tako da su preostala dva (različita) rešenja jednaka rešenju sqr(a*b). Mislim da možemo pisati da je sqr(a)*sqr(b) = sqr(a*b) imajući na umu uvek prethodne dve rečenice? da ne bude dileme, imamo w1, -w1, w2 i -w2. w1*w2 se poklapa sa rešenjem (-w1) * (-w2) a (-w1)*w2 se poklapa sa w1*(-w2). ispravno ili nije, može li iko da razjasni? Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|