Znam da postoji algoritam (1969. ga je objavio Robert Risch) koji za datu elementarnu f-ju pronalazi njenu elementarnu primitivnu f-ju (neodređeni integral) ili dokazuje da primitivna f-ja nije elementarna. Algoritam se oslanja na jedan dubok Liouville-ov rezultat.

U knjizi Algorithms for Computer Algebra, K.O. Geddes,S.R. Czapor, G. Labahn postoji vrlo detaljan opis tog algoritma, sa dovoljnim brojem primera.

Sta je elementarna f-ja?

Osnovne elementarne f-je su:
identička, konstantna, eksponencijalna, logaritamska, stepena, trigonometrijske i inverzne trigonometrijske.

Kada na njih konačno mnogo puta primeniš operacije sabiranja, oduzimanja, množenja, deljenja i kompozicije - dobijaš skup svih tzv. elementarnih f-ja.

Zaboravih da napomenem (jer sam mislio da to znaš - i izvinjavam se ako zaista znaš) da sve to ne znači da navedeni integrali ne postoje (tj. da navedene podintegralne f-je nemaju primitivnu) nego samo znači to da njihove primitivne f-je nisu elementarne.

_{[Ovu poruku je menjao uranium dana 02.04.2006. u 18:51 GMT+1]}

ok, onda koja su resenja onih integrala?

_{[Ovu poruku je menjao qzqzqz dana 02.04.2006. u 19:16 GMT+1]}

Izvini što tek sad ogovaram, ali nisam znao da si menjao poruku.

Pretpostavimo da obe podintegralne f-je posmatraš na intervalu .
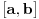
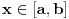
Onda za svako važi:





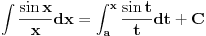
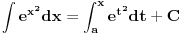
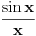
sve ovo važi zbog neprekidnosti podintegralnih f-ja (u tački f-ju možemo da dodefinišemo sa ).

Ovo nije jedini način predstavljanja rešenja, jer date f-je možemo razviti u odgovarajuće redove, a unutar njihovog radijusa konvergencije možemo ih integrisati član po član (a radijus je u ovim slučajevima beskonačan).



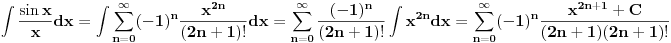
i analogno za drugi integral.

Možda će se nekome činiti da ovde imamo problem u tački , međutim za f-ju



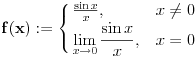
se lako dobija da važi



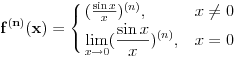
pa je f-ja beskonačno diferencijabilna i u nuli.

_{[Ovu poruku je menjao uranium dana 03.04.2006. u 02:21 GMT+1]}

jel postoji metod dokazivanja da neki integral nije resiv (da nema ono analiticko resenje)?