Opisacu samo najlaksi primer.
Da bi broj imao isti broj cifara prva mora biti 1 a zadnja 9.
Sto znaci da dobijeni broj pocinje sa 91..

Pocetni br: 1.......9
Dobijeni br: 91........

Prvi se mnozi sa 9, pa kad se pomnozi od 9*9 dobije se br 81.
Znaci pocetni broj izgleda 1......819! Nije tako! Ova osmica zavisi i od cifre koja je ispred, ali jedinica stoji tu sigurno.Znaci

Pocetni br: 1.......19
Dobijeni br: 91........1

Sada 19 (zadnje cifre pocetnog broja) mnozimo sa 9 i dobijamo 171. Stotine ne pisemo jer opet zavise od broja ispred pa dobijamo

Pocetni br: 1.......719
Dobijeni br: 91........71

itd. Problem nastaje kada treba da upisemo nulu i da sa njome mnozimo ( desice se posle desetak cifara) Uradi kombinaciju sa svih 9 cifara i videces da ce drug cifra koju trazis (za upisivanje) uvek biti ista.
Resenje je kada zavrsis niz sa 91 (pocetkom broja koji se trazi)
Stigao sam do dvadesete-tridesete cifre pa me je mrzelo dalje da racunam. Verovatno postoji manji broj, ali je nesto komplikovanije izracunati, a nemam vremena da objasnjavam pocinju mi predavanja.

Označimo traženi broj sa .

Očigledno je da zadatak ima i trivijalno rešenje:
Potražimo sada i ostala rešenja.

Dakle, neka je .
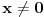
Kao što je salepronalazac i primetio poslednja cifra broja mora biti .
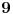
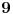
Neka broj ima cifara, onda se veza između premeštanja poslednje cifre i množenja sa može opisati jednačinom:



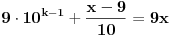
koja posle sređivanja postaje:



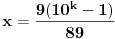
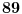
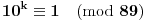
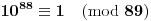
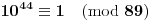
Broj je prost, i mora da važi . Na osnovu Male Fermaove teoreme znamo da je , a odatle sledi da je ili ili .
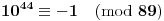
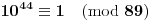
Proverom se pokazuje da je i da je to ujedno i najmanje pozitivno rešenje jednačine .

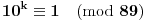
Dakle, sva rešenja su data sa , .

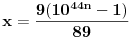
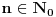
Primera radi, evo šta se dobija za :

.


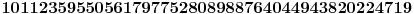
_{[Ovu poruku je menjao uranium dana 11.04.2006. u 18:12 GMT+1]}