[ Lobacev @ 13.04.2006. 09:57 ] @
| Koliko iznosi: 1. e! (e faktorijal, ili 2.71... faktorijal)? 2. i! (nije samo igra znakova, ovo znači i - imaginarna jedinica faktorijal) |
|
[ Lobacev @ 13.04.2006. 09:57 ] @
[ darkon @ 13.04.2006. 11:48 ] @
[ uranium @ 13.04.2006. 13:08 ] @
[ Lobacev @ 13.04.2006. 13:28 ] @
Baš lepo. A kakav je odgovor na pitanje 2?
[ darkon @ 13.04.2006. 14:50 ] @
Da, zaboravio sam na gama funkciju.
Međutim, ona je definisana u opštem slučaju u skupu kompleksnih brojeva, ali da bi odgovarajući integral apsolutno konvergirao, mora realan deo kompleksnog broja  biti pozitivan. Ovde je on jednak nuli, pa nisam siguran da li se u ovom slučaju integral može izračunati. U svakom slučaju treba to baciti na papir pa videti. biti pozitivan. Ovde je on jednak nuli, pa nisam siguran da li se u ovom slučaju integral može izračunati. U svakom slučaju treba to baciti na papir pa videti.[ uranium @ 14.04.2006. 21:25 ] @
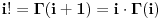 Dakle, dovoljno je da nađemo 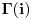 . .U knjizi On a Class of Incomplete Gamma Functions with Applications , M. Aslam Chaudhry, Syed M. Zibair postoji sledeći rezultat: 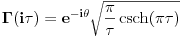 , ,pri čemu je 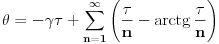 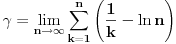 (Euler-Mascheroni-jeva konstanta) (Euler-Mascheroni-jeva konstanta)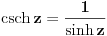 tj. hiperbolički kosekans. tj. hiperbolički kosekans.Je l' ima neki dobrovoljac da uvrsti 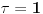 ? ? [Ovu poruku je menjao uranium dana 14.04.2006. u 22:26 GMT+1] [ Lobacev @ 17.04.2006. 07:02 ] @
Ostaje samo da proverimo da li postoji još neka funkcija f(z) za koju važi da je
f(z+1)=z*f(z) ili je Gama-funkcija jedina sa ovakvom osobinom? [Ovu poruku je menjao Lobacev dana 17.04.2006. u 10:13 GMT+1] [ uranium @ 17.04.2006. 13:39 ] @
U knjizi Functions of One Complex Variable, J. B. Conway, postoji dokaz Bohr-Mollerup-ove teoreme kojom se najčešće i karakteriše gama f-ja :
Neka je  f-ja definisana na f-ja definisana na 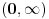 tako da je tako da je 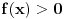 za svako za svako 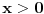 . . Ako  ima sledeće osobine: ima sledeće osobine:1. 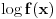 je konveksna f-ja je konveksna f-ja2. 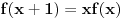 za svako za svako  3. 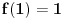 onda je 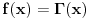 . .Ovo naravno ne daje jasan odgovor na tvoje pitanje (a odgovor na "ili - deo" je u stvari "Ne!" Posmatrajmo f-ju 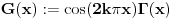 ( (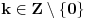 ) )Očigledno je da važi: 1. 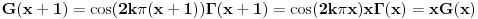 2. 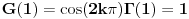 [Ovu poruku je menjao uranium dana 18.04.2006. u 03:42 GMT+1] [ Lobacev @ 17.04.2006. 14:07 ] @
Onda smo (više Uranijum nego "smo"), čini mi se, lepo apsolvirali generalisani faktorijal. Pošto je on povezan sa generalisanim izvodom (o kome je bilo već reči u nekoj od prethodnih tema), znači li to da možemo npr. naći i z-ti izvod neke funkcije (npr. sin(x)) gde je z kompleksan broj (npr. z=sqr(2)+i*sqr(2))?
[ emiraga @ 17.04.2006. 18:55 ] @
[ uranium @ 18.04.2006. 02:38 ] @
Odosmo u offtopic.
Nekoliko istorijskih činjenica: • Jacob Bernoulli u jednom od pisama Leibniz-u postavlja pitanje: Kakav bi bio smisao Leibniz-ove teoreme o  -tom izvodu proizvoda dve f-je, ako -tom izvodu proizvoda dve f-je, ako  ne bi bilo celo? ne bi bilo celo?• Leibniz u pismima L'Hôpital-u (iz 1695. god.) i Wallis-u (iz 1697. god.) primećuje da je moguće definisati izvod reda 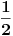 . .• Prvi uspeh postiže Euler (1738. god.) zapažanjem da 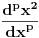 ima smisla i kad ima smisla i kad  nije celo. nije celo.• Neke zanimljive predloge dao je i Laplace (1812. god.). • Lacroix je izveo eksplicitnu formulu za 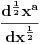 (1820. god.). (1820. god.).• Liouville (1822. god.) iznosi svoj prvi predlog definicije uopštenog izvoda, a u periodu od 1832. do 1837. objavljuje niz radova na tu temu - koji se zasnivaju na osnovnoj ideji: ako f-ju predstavimo u obliku 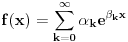 , onda je (uz izvesne pretpostavke o konvergenciji) uopšteni izvod jednak , onda je (uz izvesne pretpostavke o konvergenciji) uopšteni izvod jednak 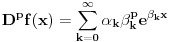 ( (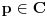 ). ).Zaista nemam živaca da pišem ovo dalje - koga ova oblast stvarno zanima (a pri kraju je sa postdipl. iz Analize [ emiraga @ 07.05.2006. 20:10 ] @
[ SrdjanR271 @ 30.12.2008. 03:44 ] @
Faktorijel od i je ovoliko 0.498016.... - i 0.15495....
Ne znam kako, ali Wolfram Matematica ga moze izracunati. [ SrdjanR271 @ 30.12.2008. 03:46 ] @
Ali znam kako dobiti 1/2 ! = SQRT[Pi]/2
[ Nedeljko @ 16.01.2009. 14:34 ] @
Faktorijel je funkcija definisana na celim nenegativnim brojevima. Produzenje je moguce, ali nije jednistveno i to onda nije faktorijel, nego nesto drugo.
[ petarm @ 17.01.2009. 10:34 ] @
Citat: SrdjanR271: Faktorijel od i je ovoliko 0.498016.... - i 0.15495.... Ne znam kako, ali Wolfram Matematica ga moze izracunati. 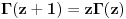 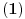 . I pozvacu se na knjigu Specijalne . I pozvacu se na knjigu Specijalnefunkcije; D. Mitronovic,D. Djokovic u kojoj je data relacija 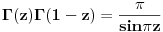 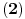 . Sada cu iz ove . Sada cu iz overelacije izraziti 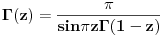 i to i toubaciti u 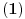 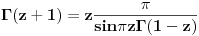 Pa Paako zamenimo 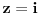 dobijamo dobijamo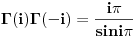 . Pa sad kad ti . Pa sad kad tiMathematica izracuna 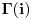 ti izracunas ti izracunas 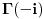 to toproveris sa rezultatom koji dobije Mathematica za 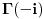 i ako i akose ta dva rezultata slazu mozes da izaberes da verujes Mathematici! :) Nadam se da nisam negde pogresio.Ja dosad u onome sto sam video u fizici nisam imao potrebu da racunam 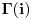 .Ali cak i da jesam .Ali cak i da jesampp da bih iskoristio Mathematicu, Mathlab ili neki slican program. Danas nema smisla raditi pesice takve stvari. To je gubljenje vremena! [ Nedeljko @ 17.01.2009. 18:58 ] @
Prvo, ovde se mešaju faktorijel i gama funkcija. Da ponovim,
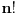 je definisano za cele nenegativne vrednosti je definisano za cele nenegativne vrednosti  . .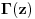 je definisano za sve kompleksne vrednosti je definisano za sve kompleksne vrednosti  izuzev celih koje nisu prirodne. izuzev celih koje nisu prirodne.Važi 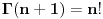 za svaki ceo nenegativan broj za svaki ceo nenegativan broj  . .Definiciju 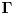 funkcije u kompleksnom području možete pronaći na funkcije u kompleksnom području možete pronaći nahttp://en.wikipedia.org/wiki/G...nction#Alternative_definitions [ petarm @ 18.01.2009. 12:46 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|