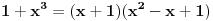
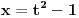
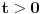
Budući da je uvodimo smenu , (neka je ) time dobijamo .

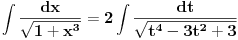
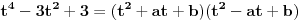
Pronađimo i takve da važi: . Dobijamo sistem:




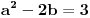
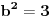
vidimo da je jedno od realnih rešenja:




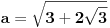
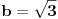
Radi jednostavnosti, neću zamenjivati te konkretne vrednosti.
Dakle, polazni integral se može zapisati u obliku .
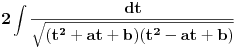
Sada nam je cilj da se uz pomoć jedne smene oslobodimo linearnih članova u oba trinoma.
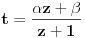
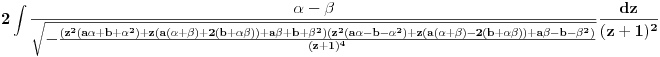
Neka je zato , integral postaje tj.



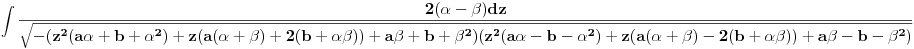
Izaberimo vrednosti za i tako da koeficijenti uz linearne članove postanu jednaki nuli. Rešavamo sistem:




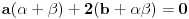
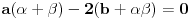
Lako dobijamo da je jedno od rešenja:




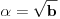
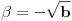
time smo integral sveli na:

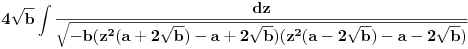
tj.



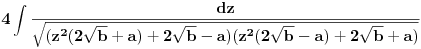
Sada potkoreni izraz svodimo na oblik:






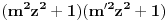
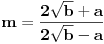
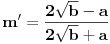
pa integral postaje:

.

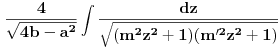
Najzad, svešćemo potkoreni izraz na oblik:

.

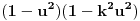
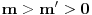
Lako se proverava da je pa možemo staviti da je




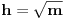
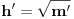
Uvodimo smenu ().
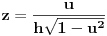
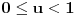
Posle sređivanja dobijamo:



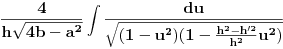
pa možemo uzeti da je .

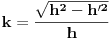
@kajla:

E sad zavisno od toga šta smatraš kanonskim oblikom - ostaje još eventualno da uvedeš smenu
().

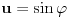
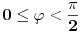
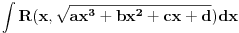
Nadam se da postoji i jednostavnija varijanta - ali ja sam "ispešačio" tipičan postupak koji (do na poslednji korak) radi za svaki eliptički integral oblika ( je proizvoljna racionalna f-ja).

Zainteresovanima preporučujem da pogledaju:

Kurs differencialnogo i integralnogo ischislenija, G. M. Fihtengolc