Malo ću promeniti oznake, tj. neka je:
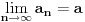
,
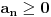
za svako
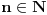
.
Ako smeš da iskoristiš neprekidnost f-je
onda odmah sledi
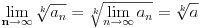
.
Pošto najverovatnije ne smeš da upotrebiš pomenutu neprekidnost - traženu relaciju
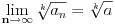
dokazujemo po definiciji limesa niza tj. dokazaćemo da za svako realno

, postoji
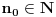
, tako da za svako prirodno

važi
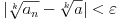 1.
1. Neka je
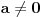
.
Prisetimo se da važi relacija:
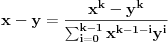
Neka je
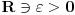
proizvoljno. Budući da važi
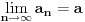
, postoji neko
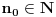
tako da za svako prirodno

važi
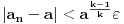
.
Sada imamo:
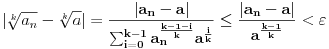
za svako prirodno

.
2. Neka je
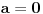
.
Onda za svako realno

, postoji
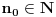
tako da za svako prirodno

važi
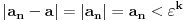
, otuda odmah sledi da svako prirodno

važi i
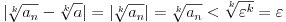
.