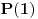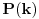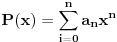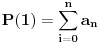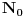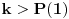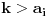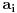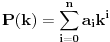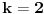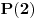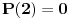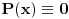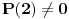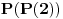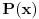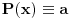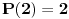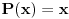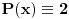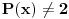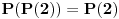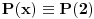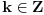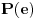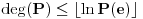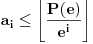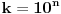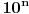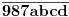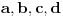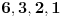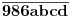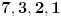|
|
[ nikmil @ 29.04.2006. 12:12 ] @
|
| Hi, folks! Prevrnuo sam net tražeći rešenja zadataka sa saveznog u Vršcu, a nema ih ni na www.imo.org.yu ni na www.matf.bg.ac.yu/~matic/competitions.
Ako neko zna gde se mogu naći rešenja, neka mi kaže, please!
[Ovu poruku je menjao nikmil dana 02.05.2006. u 19:59 GMT+1] |
[ qzqzqz @ 29.04.2006. 15:19 ] @
Mogao bi da kazes koji te zadatak zanima, pa da pokusamo svi zajedno da ga resimo. Mislim da nigde nema resenja na netu.
[ nikmil @ 29.04.2006. 18:12 ] @
Evo zadatka:
"Tatjana je zamislila polinom P(x), ciji su koeficijenti iz skupa N0.
Danica �zeli da odredi taj polinom. Ona u jednom potezu izgovara
ceo broj k, a Tatjana joj saopstava vrednost P(k). Na�ci najma�nji broj
poteza potrebnih Danici da otkrije polinom koji je Tatjana zamislila."
[ Bojan Basic @ 29.04.2006. 18:45 ] @
Ajde ja da probam, da vidimo da li sam ispao iz forme.
Najmanji broj poteza je  . Danica prvo traži vrednost 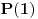 . Nakon što to sazna, pita za vrednost 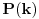 , gde je  bilo koji broj veći od 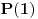 . To joj je dovoljno da otkrije o kom polinomu se radi.
Zaista, ako je 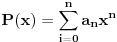 , onda je 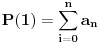 . Kako su koeficijenti iz 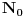 , iz 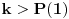 imamo 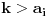 za sve 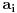 . Pošto je 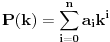 , Danica dobija koeficijente polinoma tako što zapiše 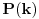 u osnovi  . [ qzqzqz @ 29.04.2006. 18:48 ] @
Verovao ili ne, najmanji broj poteza je 2.
za 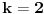 dobijamo 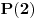 . Ako je 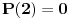 onda je 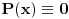 . Inace ako je 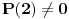 onda je 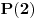 vece od svakog koeficijenta. Sada trazimo 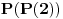 i taj broj prebacimo u sistem sa osnovom 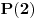 i koeficijente polinoma 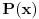 ocitamo kao "cifre" tog broja. [ Bojan Basic @ 29.04.2006. 19:15 ] @
@qzqzqz:
Imaš jednu greščicu. Ako je 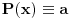 , onda 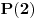 nije veće od svakog koeficijenta. To se može malo doraditi. Ako je 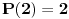 onda se dvoumimo između 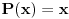 i 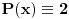 , što lako proveravamo u sledećem koraku. Ako je, pak, 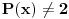 onda nastavljamo kako si rekao, uz napomenu da ukoliko dobijemo 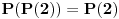 onda odmah kažemo rezultat 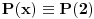 umesto da menjamo osnovu broja (što, uzgred budi rečeno, neće ni biti ispravno u ovom slučaju).
Još jedna zanimljivost. Šta ako izbacimo uslov da 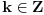 ? Onda je moguće saznati polinom u samo jednom koraku! Zaista, pitajmo za vrednost 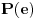 . Tada imamo 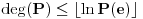 , a takođe možemo ograničiti i svaki koeficijent procenom 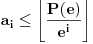 . Ostaje nam samo konačno mnogo prihvatljivih polinoma, a njih možemo isprobati jedan po jedan i videti koji se poklapa sa rečenom vrednošću. Istina, ovo bi bilo malo teže „implementirati“ u prirodi, ali i to je jedna od lepota matematike :) [ qzqzqz @ 29.04.2006. 19:38 ] @
da da, u pravu si...
[ nikmil @ 29.04.2006. 21:29 ] @
Šta da kažem, osim hvala!
Ima još jedan zadatak, koji sam rešio, ali na "rudarski" način:
"Naći najveći prirodan broj, čije su sve cifre različite, a da je djeljiv svakom svojom cifrom."
Prvo sam eliminisao cifre 0, 5 i 4, a onda sam taj broj označio kao A=9*106+8*105+7*10a+6*10b+3*10c+2*10d+1*10e.
Onda sam tražio sve kombinacije brojeva a,b,c,d,e takve da je A=0(mod 8) i A=0(mod 7), pa sam najvece A uzeo kao resenje.
Interesuje me da li postoji neki elegantniji nacin.
Poz.
[ Bojan Basic @ 29.04.2006. 22:29 ] @
Citat: #1132925/ nikmil:
Interesuje me da li postoji neki elegantniji nacin.
Nemam pojma, ali koristim priliku da istaknem da rudarski način nije ništa gori od elegantnog, jednostavno - rešenje je rešenje, pokazano je to što se traži u zadatku i kraj, svaka dalja priča je suvišna. Evo kako bih ja rešio taj zadatak: sveo bih na 7 cifara kao što si i ti učinio, a zatim bih pustio kompjuter da radi nekoliko minuta (ili sati, dana, koliko treba a zavisi i od bitnosti problema), i ispisani broj bih uzeo kao rezultat. U slučaju da se radi o nečem zvaničnom i treba da negde pošaljem/objavim rešenje, priložio bih source ili pseudo kod i nikako ne bi smeli da mi ne priznaju rešenje jer je potpuno korektno. [ Daniel011 @ 30.04.2006. 01:37 ] @
Nadovezao bih se na rešenje 1. zadatka. Možda bi bilo zgodno odabrati  tako da, uz već pomenuti uslov da je 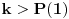 ,  takođe bude i stepen desetke, tj. 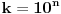 ,  . Posle toga bismo imali konverziju iz decimalnog sistema u sistem sa osnovom 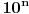 , što je mnogo jednostavije, tj. na broju zapisanom u decimalnom obliku samo posmatramo grupe od  cifara i tako dođemo do cifara odgovarajućeg broja u sistemu sa osnovom 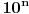 . [ Bojan Basic @ 30.04.2006. 01:46 ] @
Slažem se, ali nismo tu da olakšavamo Danici posao već samo da pokažemo da ona to može da uradi u dva poteza, a da li teško ili lako nas ne zanima - njen problem ;)
[ qzqzqz @ 30.04.2006. 08:40 ] @
Ne znam koliko je elegantije, ali moze da prodje
Posmatramo brojeve oblika 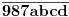 , gde su 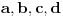 razilicite cifre iz skupa 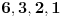 i trazimo onaj koji je deljiv sa 56. Sada koliko se secam ovde ne postoji takav broj. Onda trazimo brojeve oblika  , gde su 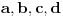 razilicite cifre iz skupa 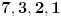 . Ovde se nadje broj koji je deljiv sa 56 i on je trazeni. [ qzqzqz @ 30.04.2006. 14:53 ] @
Cekaj bre, jesi ti siguran da bi ti priznali zadatak ako napises program?
[ Bojan Basic @ 30.04.2006. 16:02 ] @
Nisam mislio na neko takmičenje (logično, pošto tamo nemaš kompjuter da možeš da napišeš program i proveriš koje rezultate daje), već na ozbiljna matematička istraživanja. Recimo, padaju mi na pamet Problem četiri boje i Keplerova hipoteza, to su prilično čuveni problemi (a sigurno ih ima još, ako te baš zanima mogu da porazmislim). Ako se jednog dana bude promenio sistem matematičkih takmičenja tako da učenicima bude na raspolaganju kompjuter (u šta sumnjam, ali ko zna), verujem da će biti i to dozvoljeno. Na međunarodnim takmičenjima je dozvoljena i upotreba svega što je dokazano iz matematike, uz, naravno, jasnu odrednicu (o takmičenjima u zemlji neću da pričam pošto sam ove godine bio „sa druge strane stola“ i verovatno se više neću ni petljati s tim). Kad kažem „jasna odrednica“ pod tim podrazumevam da nedvosmisleno objasniš žiriju šta si koristio i odakle ti ideja da je to dokazano. Na primer, kad kažeš „Pitagorina teorema“ svi znaju da je dokazana, pa je svaka dalja referenca suvišna. Isto važi i za Veliku Fermaovu teoremu (da, sme se slobodno koristiti, bez obzira na to što je dokaz takav kakav jeste). S druge strane, može da ti zatreba i nešto što nije baš opštepoznato, i tu je potrebno da navedeš makar autora i naziv rada, a poželjno je da staviš i naziv i broj časopisa u kom je rad objavljen kako niko ne bi imao problema da proveri to što pričaš. Tu su takmičari opet u hendikepu jer nemaju na takmičenju mogućnosti da proveravaju koji rezultati koji su im potrebni su objavljeni, ali ako nekad naletiš na nešto za šta misliš da će ti zatrebati nauči napamet referencu i samo je citiraj. Postoji primer sa IMO u Moskvi kada je jedan takmičar koristio teoremu iz teorije grafova i zahvaljujuži njoj rešio zadatak. U blizini je bilo dosta stručnjaka iz teorije grafova ali niko nije znao za tu teoremu, no nisu uspeli da nađu ni kontraprimer. Pošto je žiri bio dobro raspoložen zvali su telefonom u Ameriku najvećeg stručnjaka iz te oblasti, i čak ni on nije znao da li je teorema tačna ili ne. Pošto je žiri bio ekstremno dobro raspoložen bacili su se sami na rešavanje, i jedan koordinator je pri kraju drugog dana uspeo da konstruiše kontraprimer, pa je učenik dobio zasluženih 0 bodova. Da je žiri dokazao teoremu, po rečima jednog poznatog tim lidera, učenik bi najverovatnije dobio 7 bodova. To je ujedno i mana korišćenja takvih rezultata - ako imaš makar i najsitniju greščicu treba da se pomučiš i za bod, no ako si siguran da ti je sve dobro možeš mirno da spavaš. Za ovaj gornji primer sam samo čuo, ali imam i jedan koji znam iz prve ruke (pričao mi je takmičar koji je tako uradio). Olimpijada 1991, zadatak B3. On je koristio jedan uslov za konvergenciju Zeta funkcije. Uslov je relativno poznat, ali složićeš se da baš nije primeren način rešavanja zadatka sa srednjoškolskog takmičenja. Bilo je diskusije u žiriju (samo on i jedan Mađar su tako uradili), i na kraju je došao predsednik, pogledao o čemu se radi, i rekao: „Gospodo, šta da se radi, ne valja vam zadatak kad može tako da se reši, rešenja su potpuno tačna i moramo dati po 7 bodova“. Kako izgleda kad se zadatak rešava uz pomoć slabo poznatih rezultata možeš videti ovde (drugi način) i ovde. [ qzqzqz @ 02.05.2006. 17:36 ] @
Zanimljivi su ti ovi primeri... Nego, kada bi mi ostalo na takmicenju da proverim da li nesto vazi za nekoliko stotina brojeva i opisem to nekim algoritmom ja mislim da bi morali da mi daju nesto za taj deo zadatka. Ipak je to skoro zavrsen zadatak koji je logicki ispravno uradjen.
[ darkon @ 02.05.2006. 18:34 ] @
Teško da ćeš ih ovde ikada naći ;) [ nikmil @ 02.05.2006. 19:01 ] @
Citat: darkon: Teško da ćeš ih ovde ikada naći ;)
Moja greska. Mislio sam www.imo.org.yu[ Bojan Basic @ 02.05.2006. 19:12 ] @
Citat: qzqzqz:
Zanimljivi su ti ovi primeri... Nego, kada bi mi ostalo na takmicenju da proverim da li nesto vazi za nekoliko stotina brojeva i opisem to nekim algoritmom ja mislim da bi morali da mi daju nesto za taj deo zadatka. Ipak je to skoro zavrsen zadatak koji je logicki ispravno uradjen.
Na IMO da, možda bi čak mogao da dobiješ i sve. Na nacionalnim takmičenjima sumnjam da ćeš mnogo postići, neću mnogo da pričam o tamošnjim dešavanjima, ali reći ću ovako: član sam republičke i savezne komisije iz informatike, i tamo je milina raditi - svako smisli po nekoliko zadataka (a i ne mora ako nema ništa, uvek bude dovoljno predloga), sastanemo se jedan dan, prodiskutujemo predloge, odaberemo koliko treba i to je ceo posao. Što se tiče matematike to ide... malo drugačije. Za pregledanje je tek posebna priča - na moje oči se učenik žali što su mu skinuli 5 bodova (ili beše čak 10, ne sećam se) na potpuno tačan zadatak (pregledao sam taj njegov zadatak nekoliko puta i apsolutno tvrdim da je zadatak 100% korektan), i oni kažu da mu fali neki primer. On zaokruži jednu rečenicu i kaže da je to primer (naravno, jeste), dok se oni blesave i kažu da to nije to. I, kao vrhunac svega, pošto je učenik bio uporan, oni njemu kažu: "Da si bar napisao da je to primer bilo bi dobro, ali nigde to ne piše". Sve sam znao kako to ide i dok sam se takmičio ali tad sam se borio za svoj groš i imao sam više živaca da se svađam sa... članovima komisije, sad je malo drugačije. Naravno, ima tamo i OK ljudi, ali su manjina i ništa ne mogu da urade. Nadam se samo da će se stvari uskoro promeniti, u suprotnom ja zauvek okrećem leđa nacionalnim matematičkim takmičenjima srednjoškolaca iako bi mi bilo jako žao jer stvarno to volim da radim.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|