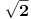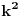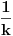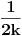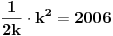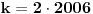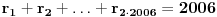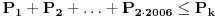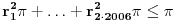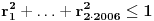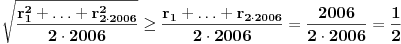[ nikmil @ 15.05.2006. 13:45 ] @
|
| Na republičkom takmičenju CG (12. maj, Nikšić) bio je sledeći zadatak:
- Dokazati da se u krug poluprečnika 1 može smestiti 2*2006 krugova, tako da nijedan krug nema zajedničku unutrašnju tačku sa ostalim krugovima, a da im je zbir poluprečnika jednak 2006.
Ovaj zadatak ima dva SUPROTNA rešenja, jedno kojim se dokazuje tvrđenje, a jedno kojim se to tvrđenje obara. Oba rešenja izgledaju logično i tačno, ali sigurno je da ne mogu biti oba tačna, pa vas molim za pomoć da nađemo koje je pogrešno. Evo kako idu rešenja
1: U krug poluprečnika 1 može se upisati kvadrat stranice 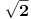 , pa samim tim i kvadrat stranice , pa samim tim i kvadrat stranice  . Ako taj kvadrat izdjelimo na . Ako taj kvadrat izdjelimo na 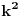 kvadrata, stranica kvadrata, stranica 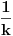 i u njih upišemo krugove, poluprečnici tih krugova će biti i u njih upišemo krugove, poluprečnici tih krugova će biti 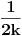 . Ako uzmemo da je zbir poluprečnika, prema uslovu iz zadatka, jednak 2006, dobijamo: . Ako uzmemo da je zbir poluprečnika, prema uslovu iz zadatka, jednak 2006, dobijamo:
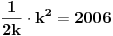 , tj. , tj.
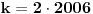 , iz čega sledi da se može smestiti 2006*2 krugova da im je suma poluprečnika 2006. , iz čega sledi da se može smestiti 2006*2 krugova da im je suma poluprečnika 2006.
Ovo je, inače, bilo zvanično rešenje komisije.
2: Ako uzmemo da postoje ti krugovi i označimo ih sa  , a prvi (dati) krug sa , a prvi (dati) krug sa  onda je: onda je:
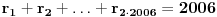 . .
Da bi manji krugovi bili smesteni u veći, dati krug, mora da je zadovoljeno:
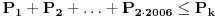
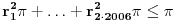
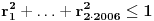 . .
Koristeci nejednakost kvadratne i aritmeticke sredine dobijamo:
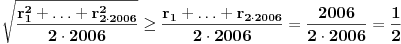 , tj. , tj.
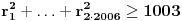 , sto je u kontradikciji sa , sto je u kontradikciji sa 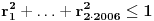 , pa krugovi , pa krugovi  ne mogu postojati. ne mogu postojati.
Ovo je bilo moje resenje zadatka, na koje sam dobio max. 25 poena, ali bih da resim dilemu koje je resenje ispravno. |
[ cassey @ 15.05.2006. 14:46 ] @
Koliko ja vidim, u prvom resenju ti upises k^2 krugova tj. (2 * 2006)^2 krugova a ne 2 * 2006 krugova...
[ Bojan Basic @ 15.05.2006. 15:21 ] @
Ako si dobio 25 poena na rešenje koje daje različit rezultat od zvaničnog to bi trebalo da znači da je komisija pronašla grešku u svom rešenju (onu na koju je Andreja ukazao) i tvoje ocenila kao tačno. Verovatno je još takmičara pronašlo rešenje kao tvoje pa je komisija jednostavno primetila da njihovo ne valja.
[ nikmil @ 15.05.2006. 16:53 ] @
Vidi baš. Kakav previd.
... ha... Hvala momci
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.