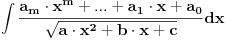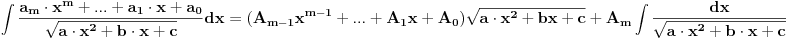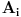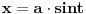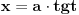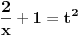[ ponta @ 15.05.2006. 14:17 ] @
| Nakon što sam se ganjao sa 3 profesora, 10 asistenata i mali milion studenata (oni bolji), evo me i kod vas. Ostao mi je usmeni iz matematike, kojeg sam 90% uradio. Ali da tu nisu ti integrali:( Zamolio bi bilo koga ko zna uraditi ove zadatke da mi pomogne. Jer ja sam sve pokušao ali ne nalazim rješenje. Ako neko može makar da me uputi kako da ih uradim, jer mi ovisi godina od ovih zadataka. HVALA unaprijed svim dobrovoljcima inegral ((x^2-x+1)dx)/(sqrt(x^2+2*x+2)) integral sqrt(x^2+2*x)dx |