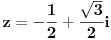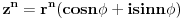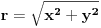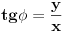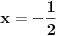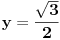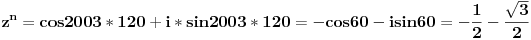[ TheAlas @ 15.05.2006. 19:18 ] @
|
| Moze li neko da mi pomogne u resavanju ovog kompleksnog broja?
( (sqrt(3)/2)*i - 1/2 )^2003
Ne mogu nikako da shvatim o cemu se radi, eksponent broja samo menja znakove, ali ne znam zasto niti kako to da koristim. Resenje zadatka je:
-1/2 - (sqrt(3)/2)*i
dakle isto kao i bez exponenta - imaginarni deo je samo promenio znak, takodje se dobija isto resenje kvadriranjem (zamenio sam 2003 sa 2)...
O cemu se ovde radi?  |
[ mickey6252 @ 15.05.2006. 19:44 ] @
Pokušaj da taj broj prebaciš u eksponencijalni oblik. Koliko vidim, ovako s nogu, modul ovog broja je 1, pa će i rešenje biti na jediničnoj kružnici.
[ zarkomd @ 15.05.2006. 19:59 ] @
to mu dodje
(1*exp(i*(2pi/3))^2003= exp(i*2*2003pi/3)=cos(pi*4005/3+pi/3)+i*sin(pi*4005/3+pi/3)=-1/2-I*sqrt(3)/2
[ jelena-dj @ 16.05.2006. 13:45 ] @
Imamo
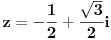
Primeni Moavrovu formulu za stepenovanje kompleksnog broja:
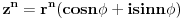
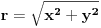
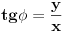
gde je
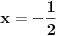
, a
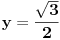
dobijamo da je r=1, a phi=120 stepeni (posto je rec o drugom kvadrantu)
i kad to sve zamenimo:
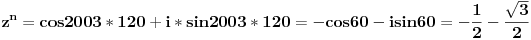
POZDRAV!
[ TheAlas @ 17.05.2006. 18:51 ] @
Hvala ljudi (a posebno Jeci

), nisam znao za Moavrovu formulu - sad je sve jasno

.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.