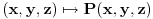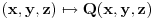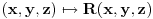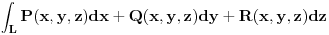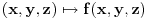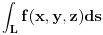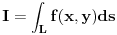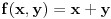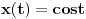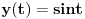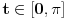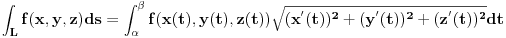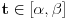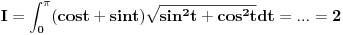Nisi baš najjasniji. Za potpunu definiciju krivolinijskog integrala obratićeš se nekom relevantnom udžbeniku, npr.

Matematika III, kratak kurs profesora Dobrila Tošića.

Siguran sam da postoji još dosta udžbenika na ovu temu gde je ova tematika i podrobnije obrađena.

Ja ću ovde samo ispisati definicije krivolinijskog integrala po koordinatama (krivolinijski integral druge vrste), krivolinijskog integrala po luku (krivolinijski integral prve vrste) i rešiću drugi primer iz tvoga posta.

1. Krivolinijski integral druge vrste:

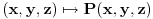
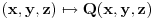
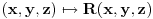
Uz odgovarajuću definiciju luka i date funkcije , i definisane u svakoj tački luka , krivolinijski integral druge vrste se piše ovako:



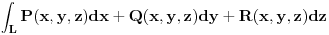
2. Krivolinijski integral prve vrste:

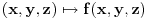
U ovom slučaju luk ne mora biti orijentisan. Funkcija je definisana u svim tačkama luka , pa je krivolinijski integral prve vrste:

,

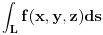
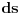
gde je priraštaj luka u graničnom procesu.

Iz nekog razloga tebe zbunjuju neke pozitivne vrednosti. Evo rešenja drugog zadatka:

ZADATAK: Rešiti krivolinijski integral:

,
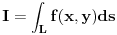
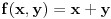
gde je , a luk je definisan kao gornja polovina kružnice (y>0) sa centrom u koordinatnom početku.

REŠENJE:

Luk možemo zapisati u parametarskom obliku:
,
,

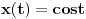
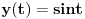
gde je .

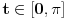
Krivolinijski integral prve vrste se rešava pomoću formule:

,
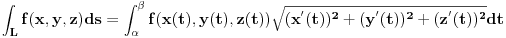
gde je .

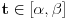
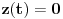
U našem slučaju je , pa dobijamo:



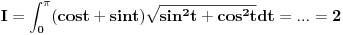_{[Ovu poruku je menjao darkon dana 03.06.2006. u 17:03 GMT+1]}

Hvala! Moze li pomoc oko ovog zadatka.

1.) Izracunajte krivolinijski integral integral od (dx-dy)/(x+y) uzet duz konture kvadrata s temenima u tackama A(1,0), B(0,1), C(-1,0) I D(0,-1) pod uslovom da se kontura obilazi u smeru suprotnom od smera kazaljke na satu.

Iscepkam ovaj integral na cetiri po AB,BC,CD i DA i dobijem da su integrali po BC i DA jednaki nuli. Ali sta dalje? U napomeni pise da se ne moze koristiti Greenova formula. Zasto? Unapred hvala!

Doduse ovo je krivolinijski integral druge vrste! Ali mislim da nije neki problem sto sam ovde postavio. Uzgred na tom mestu gde su formule pojave mi se crna slova koja ne mogu procitati! Sta da radim?

Pa saberi integrale po konturama AB i CD i treba da dobiješ rezultat -4. Nemoguće da si zaključio ovo gore, a da ne znaš da rešiš ova dva integrala. Ako je baš toliki problem, postovaću kompletno rešenje ovde.

Greenova formula se bavi integracijom po zatvorenoj orjentisanoj površini, što ovde nije slučaj.

Na kom mestu? O kojim formulama govoriš?

Shvatio sam! Hvala ti! Ovo sam odmah video da je npr. kod BC y-x=1, pa kad sam diferencirao dx-dy=0. Odakle mi je odmah brojilac bio jednak nuli, pa i sam integral od B do C. Isto to dobijem i kod DA. Ne znam zasto nisam odmah parametrizovao AB y=t, x=1-t, dy=dt, dx=-dt i isto tako i kod CD. U redu je –4. Zasto kazes da kontura nije orijentisana ako je u zadatku dato da je obilazim u smeru suprotnom od smera kazaljke na satu. To sto pises u TEXU ne mogu da procitam, od danasnjeg dana. Ne znam zasto. Pojavi mi se crn okvir oko formule I veoma sitna bela slova I kada na to kliknem pojavi mi se zapis ali u Texu.

U slučaju krivolinijskih integrala prve vrste sam rekao da luk (kontura) ne mora biti orijentisan. U rešenom zadatku se radi o krivolinijskom integralu druge vrste i očigledno da od smera konture zavise granice određenih integrala.

Što se tiče problema sa TEX-om ne mogu ti pomoći. Ja sve vidim OK.
Ima li još neko problema sa nečitljivošću formula?

I još nešto: valjanost rezultata gornjeg problema bi trebalo biti moguće proveriti Stokes-ovom formulom.