Neka je , onda prema prvom uslovu imamo , a prema drugom uslovu imamo .

Ako je , onda važi .
Specijalno, ako je , onda je i pa važi .

Za svako celo i važi .
()

Dakle, ako bi bilo i i , onda bismo imali da je , pa bi moralo da bude a to je kontradikcija.

Znači, mora biti ili .

Ne može biti , jer bi to (u slučaju da je ) vodilo ka što je kontradikcija.

Najzad, vidimo da je tj. .

Neka je , onda imamo tj.
- pošto ovo poslednje mora da važi za svako jasno je da mora biti .

Dakle, jedino rešenje je

Lepo, čestitam.

Evo i moja dva obećana rešenja.

Rešenje 1:

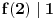
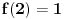
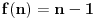
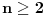
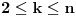
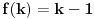
Iz prvog uslova zadatka za dobijamo iz čega direktno sledi . Dokazaćemo indukcijom da je za sve . Neka za svako važi . Kako je

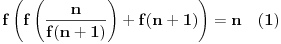
sledi da je

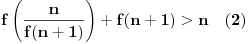
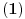
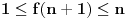
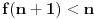
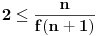
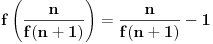
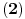
(u suprotnom bi, na osnovu induktivne hipoteze, leva strana relacije bila manja od ). Očigledno je . Pretpostavimo da je . Sada je pa na osnovu induktivne hipoteze imamo . Uvrštavanjem ovoga u imamo:



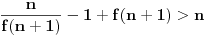
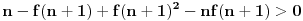
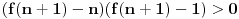
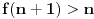
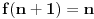
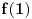
Izraz u drugoj zagradi je nenegativan pa je što je kontradikcija. Sledi da je pretpostavka netačna pa mora biti . Preostaje još da nađemo vrednost . Imamo da je

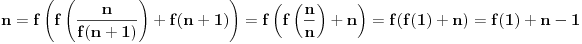
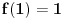
iz čega sledi . Lako se proverava da funkcija

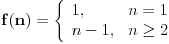
zaista ispunjava uslove zadatka.

Rešenje 2:

Iz prvog uslova zadatka sledi

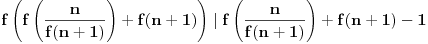
što u kombinaciji sa drugim uslovom daje

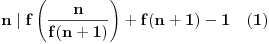
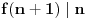
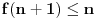
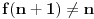
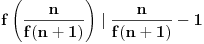
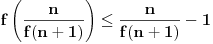
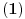
Pošto sledi da je . Slično, ukoliko pretpostavimo da za neko važi , iz sledi , i uvrštavanjem dobijene dve nejednakosti u relaciju dobijamo

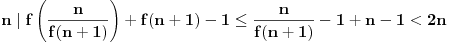
Dakle, da bi važila naznačena deljivost mora biti




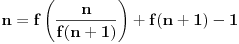
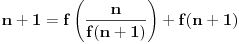
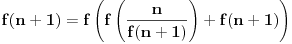
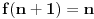
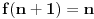
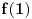
Ovo je kontradikcija sa našom pretpostavkom. Zaključili smo da za svako važi . Preostaje još da nađemo vrednost , a ovo se radi isto kao u prethodnom rešenju.

Lep zadatak Basicu.. .Sto ga nisi sacuvao za naredne godine?

Ako nije prošao ove godine verovatno iz istog razloga ne bi ni neke naredne (predlagao sam ga za republičko, tu je bio previše težak, onda posle za savezno, tu ne znam šta beše razlog). Osim toga, prilično sam se razočarao u situaciju u Društvu matematičara (kao što sam jednom rekao, i dok sam bio takmičar znao sam da je loše, ali nisam znao da je baš ovoliko loše) pa ne znam ni da li ću se više baktati tim, a ako i budem odlučio da nastavim, do sledeće godine ću verovatno smisliti još zadataka - nije mi neophodno da čuvam baš ovaj jedan.

A kome ti uopste predlazes i saljes zadatak kad ga smislis?

Daš nekome koga poznaješ a ko ide na sastanak povodom izbora zadataka (naravno, moraju svi da znaju ko si zbog garancije da nisi nikome rekao).