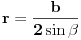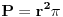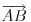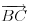[ mrakodol @ 08.06.2006. 16:18 ] @
| 1.Dati su prirodan broj n(n>3) i skup A od n tacaka u ravni. Odrediti tri razlicite tacke skupa A tako da razlika izmedju povrsine kruga ogranicene kruznicom koja prolazi kroz prolazi kroz te tri tacke i povrsina trougla sa tjemenima u tim tackama bude najmanja. Ako takvih trojki tacaka ima vise onda ih odrediti sve. 2.Dati su prirodni brojevi m i n, i polinom P(x) stepena n svojim koeficientima uz X (na i) , a i=0,1,2,...,n. Odrediti koeficiente polinoma P(na m)(x) razvijenog po stepenima od x. *P(na m)(x)-citati P na m od x **X (na i)-citati X na i Ovi zadaci su mi za zadacu pa vas molim da mi pomognete!Ili barem matematicki objasnite kako bi se to moglo rijesiti a sam cu da pisem program..jednostavno ne razumijem teks zadatka! |