Može štapom i kanapom :)
Funkciju
g(
x) rastaviš na dve:
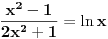
Onda ispitaš ovu racionalnu funkciju, i videćeš da, na domenu [1, +∞):
1. ima nulu u tački
x = 1, a nagib u toj tački manji od 45º
2. ima horizontalnu asimptotu
x = 1/2
3. svuda je konveksna
ln(
x) je takođe svuda konveksna i ima nulu u tački
x = 1, ali je nagib u toj tački tačno 45º.
Drugim rečima, ln(
x) je svuda iznad ove racionalne funkcije, pa je funkcija
g(
x) svuda negativna.