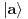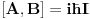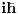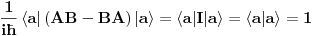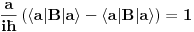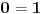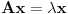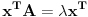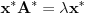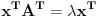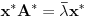[ tomkeus @ 10.06.2006. 14:19 ] @
|
[ tomkeus @ 11.06.2006. 16:47 ] @
Nema zainteresovanih za diskusiju? :(
[ Lobacev @ 12.06.2006. 11:06 ] @
Možda zato što se formule slabo vide!!!
[ tomkeus @ 12.06.2006. 15:11 ] @
Ne znam. Meni normalno izgledaju.
[ Daniel011 @ 14.06.2006. 01:42 ] @
Formule se slabo vide iz Internet Explorera, dok se iz Opere vide normalno. Na ovaj problem sam ukazao u ovoj temi, ali nažalost još uvek niko nije reagovao po pitanju rešavanja tog problema.
Izvinjavam se zbog offtopic-a. [ Mikky @ 26.10.2008. 21:49 ] @
Jel moze pojasnjenje gde je greska u gornjem rezonovanju?
[ petarm @ 27.10.2008. 19:59 ] @
Ipak Nedeljko zadatak sadrzi rec OPSERVABLA! Observable u kvantnoj mehanici predstavljene su ermitskim operatorima, a svojstvene vrednosti ermitskih operatora su realne!
[ petarm @ 27.10.2008. 20:02 ] @
[ tomkeus @ 29.10.2008. 16:20 ] @
Citat: petarm: Ipak kako su ove opservable kanonski konjugovane one imaju neprekidan spektar pa vektor 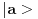 ne moze biti normiran na ne moze biti normiran na  :) :)Tačno tako. Ovo je u principu dokaz kontradikcijom da kanonski konjugovane opservable nemaju diskretan spektar. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|