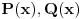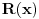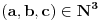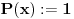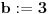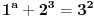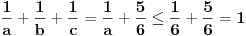[ qzqzqz @ 13.06.2006. 19:27 ] @
|
[ Bojan Basic @ 13.06.2006. 21:00 ] @
Teško da mi to možemo ovde dokazati. Glavni kamen spoticanja nije Velika Fermaova teorema (iako si pokazao da Zadatak nju implicira, možda bi se moglo pokazati i obrnuto, tj. da ona implicira Zadatak što bi bilo sasvim legitimno rešenje jer je ona dokazana i sme se kao takva koristiti). Ono što nam ovde zaista pravi problem je što Zadatak implicira i jedan prilično težak otvoren problem, Beal's Conjecture.
Zaista, neka smo dokazali tvrđenje. Pretpostavimo da postoje  i i 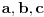 za koje je za koje je 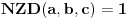 takvi da je takvi da je 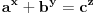 . U tom slučaju je . U tom slučaju je 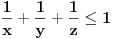 , što je u suprotnosti sa Zadatkom za , što je u suprotnosti sa Zadatkom za  , ,  , ,  , , 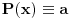 , ,  , , 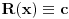 . .Nego, zanima me da li je ovo nešto za šta se veruje da je tačno ili ti je palo na pamet? Ako je ovo drugo javi, pa možda možemo naći kontraprimer. [ qzqzqz @ 13.06.2006. 21:11 ] @
Pa ja mislim da je ovo tacno jer je danas na dodatnoj Dusan Djukic dokazao ovo. Manje-vise sam skontao, pa ako nekog zanima iznecu dokaz.
[ Bojan Basic @ 13.06.2006. 22:04 ] @
E, ako možeš bilo bi super da vidimo dokaz (ako se ne sećaš celog i samo smernice bi pomogle), koliko poznajem Đukića on zna šta priča.
[ uranium @ 14.06.2006. 02:17 ] @
[ qzqzqz @ 14.06.2006. 06:20 ] @
Glavna fora je u tome sto se koristi sledeca lema:
Neka su 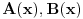 i i  uzajamno prosti polinomi takvi da je uzajamno prosti polinomi takvi da je 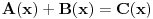 . .Onda je 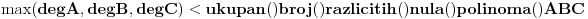 . .Ova lema se primeni na polinome 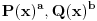 i i 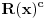 i dobija se zadatak. i dobija se zadatak.E sad dokaz ideo nekako ovako: Neka je  , slicno i za , slicno i za 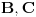 . .Imamo da je  . Sada obe strane diferenciramo i dobija se nesto oblika . Sada obe strane diferenciramo i dobija se nesto oblika 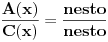 , pa posto su A i C uzajamno prosti posle svodjenja na zajednicki A je ovo gore, a C je dole. Samo sto ovo , pa posto su A i C uzajamno prosti posle svodjenja na zajednicki A je ovo gore, a C je dole. Samo sto ovo  nisam prepisao. Posle ovoga sledi i lema. nisam prepisao. Posle ovoga sledi i lema.Sada neka neko dopuni ovaj dokaz. [ Bojan Basic @ 14.06.2006. 13:47 ] @
Citat: uranium: priznajem da sam možda malo zloupotrebio nepreciznost postavke... :) Možda sam nešto prevideo, ali gde tačno si zloupotrebio nepreciznost postavke? Meni ovo deluje kao sasvim legalan kontraprimer. @qzqzqz: Više stvari mi nije jasno pa ću da krenem sa jednom po jednom. Citat: qzqzqz: pa posto su A i C uzajamno prosti posle svodjenja na zajednicki A je ovo gore, a C je dole. Nigde nismo rekli da su A i C uzajamno prosti, rekli smo samo da je 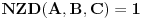 . Verovatno si hteo da u formulaciji kažeš da su . Verovatno si hteo da u formulaciji kažeš da su 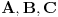 uzajamno prosti po parovima (to znači da su svaka dva od njih uzajamno prosti), da li sam u pravu? uzajamno prosti po parovima (to znači da su svaka dva od njih uzajamno prosti), da li sam u pravu?Citat: I dalje ne vidim kako, možeš li još malo da pojasniš? Citat: Ovo mi deluje najnelogičnije. Evo jednog kontraprimera, pa ti vidi šta nije u redu (čak i ako usvojimo moju prvu ispravku). Neka je 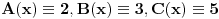 . Ovi polinomi su uzajamno prosti (štaviše, po parovima), i važi da je . Ovi polinomi su uzajamno prosti (štaviše, po parovima), i važi da je 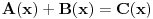 , pa je ipak , pa je ipak 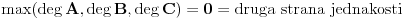 . .Da li imaš slučajno zabeleženo još nešto ili se sećaš još nečega što nisi pomenuo a moglo bi da razjasni ove nedoumice? Hoćeš li da pitam Đukića šta je tačno predavao pa da javim? [ qzqzqz @ 14.06.2006. 14:29 ] @
Pa u pravu si, najbolje je da njega pitas, a ne da ja dajem polu-tacne informacije.
[ uranium @ 14.06.2006. 14:35 ] @
Znao sam da ću se kajati zbog ovoga
Pitanje je sasvim na mestu, međutim ja sam se krajnje neprecizno izrazio... Kontraprimer je sasvim u redu pod uslovom da je formulacija tvrđenja upravo onakva kako ju je qzqzqz i napisao. Aludirao sam na to da tvrđenje(?) možda treba posmatrati do na neke trivijalne slučajeve. Što se tiče same leme, ukoliko se dokaz glavnog tvrđenja bitno oslanja na strogu nejednakost - onda je ona smena  potpuno nekorektna, jer kao što vidimo lema (u sadašnjoj formi) ne važi za ne-nula konstantne polinome. potpuno nekorektna, jer kao što vidimo lema (u sadašnjoj formi) ne važi za ne-nula konstantne polinome. Meni se čini da kada uzmemo da je 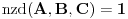 a pri tom i a pri tom i 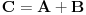 da su onda polinomi uzajamno prosti i po parovima. da su onda polinomi uzajamno prosti i po parovima.Onaj deo sa izvodima mi deluje veoma sumnjivo - ako ništa drugo, mislim da bi bilo neophodno dokazati i da su  i i  uzajamno prosti - pre nego što izvučemo zaključak uzajamno prosti - pre nego što izvučemo zaključak  i i 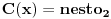 . Nažalost, ključni problem nastaje mnogo ranije - naime ako smo već uzeli da je . Nažalost, ključni problem nastaje mnogo ranije - naime ako smo već uzeli da je 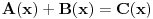 tj. tj.  onda diferenciranjem obe strane identiteta ne možemo ni očekivati da dobijemo nešto korisno. Zaista posle sređivanja (imajući u vidu onda diferenciranjem obe strane identiteta ne možemo ni očekivati da dobijemo nešto korisno. Zaista posle sređivanja (imajući u vidu 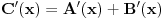 ) dobijamo: ) dobijamo: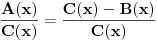 . .Sve u svemu, nije mi ni izbliza jasna veza između leme i glavnog tvrđenja. [ qzqzqz @ 16.06.2006. 14:42 ] @
Evo tacnog tvrdjenja zadatka i leme(zadatak 13.)
http://www.matf.bg.ac.yu/~mati...ne/polinomskejednacine_ddj.pdf [ Bojan Basic @ 16.06.2006. 15:04 ] @
Sinoć mi je poslao link ka tome kad sam ga pitao za tačnu formulaciju i rešenje i jutros sam čitao ali nisam uspeo da razumem neke stvari, recimo zašto je koeficijent uz vodeći stepen polinoma po pretpostavci jednak jedinici?
Citat: uranium: Meni se čini da kada uzmemo da je 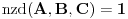 a pri tom i a pri tom i 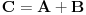 da su onda polinomi uzajamno prosti i po parovima. da su onda polinomi uzajamno prosti i po parovima.Ovde si u pravu, nisam obratio pažnju na to. [ uranium @ 16.06.2006. 17:20 ] @
Moram da priznam da je rešenje zaista prelepo
...dakle, ono diferenciranje je ipak donelo neke korisne informacije  , već (a to je sasvim dovoljno) , već (a to je sasvim dovoljno)  . .Nemam nikakve zamerke na rešenje (s tim da je u formulaciji i zadatka i leme trebalo naglasiti da se radi o polinomima stepena barem 1). @Bojan Bašić: To što su svi polinomi monični - mislim da nije nikakav problem, jer (koliko vidim) dokaz leme bi tekao isto i u protivnom. [ Bojan Basic @ 16.06.2006. 18:45 ] @
Citat: uranium: To što su svi polinomi monični - mislim da nije nikakav problem, jer (koliko vidim) dokaz leme bi tekao isto i u protivnom. Čini se da si u pravu ali svakako može da unese zabunu, mislim da je ipak potrebno bar napomenuti. Citat: uranium: Nemam nikakve zamerke na rešenje (s tim da je u formulaciji i zadatka i leme trebalo naglasiti da se radi o polinomima stepena barem 1). Eto, posle svega je zadatak korektan (i vrlo lep) uz dodatne uslove, ali ipak ništa od Velike Fermaove teoreme ni Bealove hipoteze :) Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|