[ useer @ 20.06.2006. 11:24 ] @
| da li neko moze da mi pokaze resenje 3. zadatka sa IMO 2004... video sam neko resenje na mathlinksu ali tamo nista nisam mogao da skontam, ruzna im je grafika |
|
[ useer @ 20.06.2006. 11:24 ] @
[ Bojan Basic @ 21.06.2006. 13:11 ] @
Zadatak:
Nazovimo kukom figuru sastavljenu od 6 jediničnih kvadrata kao na slici. 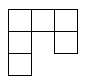 Odrediti sve 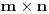 pravougaonike koji se mogu pokriti kukama. Pravougaonik pokrivamo bez preklapanja i bez rupa, nijedan deo kuke ne sme da izađe van pravougaonika, i kuke smemo slobodno okretati i prevrtati. pravougaonike koji se mogu pokriti kukama. Pravougaonik pokrivamo bez preklapanja i bez rupa, nijedan deo kuke ne sme da izađe van pravougaonika, i kuke smemo slobodno okretati i prevrtati.Rešenje: Pravougaonik se može pokriti u samo sledećim slučajima: 1) 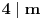 , , 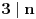 ; ;2) 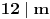 , , 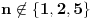 (ili isto ovo sa zamenjenim 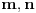 ). ).Pretpostavimo da je neki 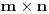 pravougaonik već pokriven na opisani način. Najpre uočimo da svakoj kuki možemo pridružiti neku drugu koja pokriva njeno „unutrašnje“ polje. Pri tome je očigledno da je ovakvo pridruživanje uzajamno, tj. da smo time podelili skup kuka na parove tako da svaki par obrazuje jednu od sledeće dve pločice. pravougaonik već pokriven na opisani način. Najpre uočimo da svakoj kuki možemo pridružiti neku drugu koja pokriva njeno „unutrašnje“ polje. Pri tome je očigledno da je ovakvo pridruživanje uzajamno, tj. da smo time podelili skup kuka na parove tako da svaki par obrazuje jednu od sledeće dve pločice.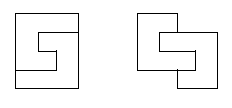 Pošto se svaka pločica sastoji od 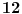 jediničnih kvadrata, odmah zaključujemo da jediničnih kvadrata, odmah zaključujemo da 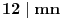 . Pretpostavimo da je jedan od . Pretpostavimo da je jedan od 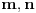 deljiv sa deljiv sa  , i neka, bez umanjenja opštosti, , i neka, bez umanjenja opštosti, 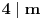 . Ako pri tome i . Ako pri tome i 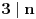 , polazni pravougaonik možemo razbiti na pravougaonike veličine , polazni pravougaonik možemo razbiti na pravougaonike veličine 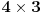 , od kojih svaki možemo lako pokriti. , od kojih svaki možemo lako pokriti.Dalje, ako 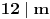 i i 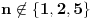 , uvek postoje , uvek postoje 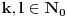 takvi da je takvi da je 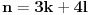 (rezultat Silvestera) pa u tom slučaju pravougaonik izdelimo na delove (rezultat Silvestera) pa u tom slučaju pravougaonik izdelimo na delove 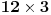 i i 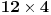 od kojih svaki možemo pokriti kao što je već pokazano, a u slučaju od kojih svaki možemo pokriti kao što je već pokazano, a u slučaju 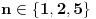 očigledno je da traženo pokrivanje ne postoji. očigledno je da traženo pokrivanje ne postoji.Preostao nam je još slučaj 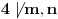 . Tada su . Tada su  i i  parni brojevi, a broj pločica je neparan. Obojmo svaku četvrtu kolonu u crno, svaki četvrti red u crno, a preseke ovih obojenih redova nećemo obojiti. Primetimo da svaka pločica pokriva neparan broj obojenih kvadratića i ima ih neparan broj, a ukupno ima parno obojenih kvadratića. Kontradikcija. parni brojevi, a broj pločica je neparan. Obojmo svaku četvrtu kolonu u crno, svaki četvrti red u crno, a preseke ovih obojenih redova nećemo obojiti. Primetimo da svaka pločica pokriva neparan broj obojenih kvadratića i ima ih neparan broj, a ukupno ima parno obojenih kvadratića. Kontradikcija.[ useer @ 21.06.2006. 13:37 ] @
mnogo lep zadatak ...
hvala bojane ...nego kako mogu da te pitam nesto ako jos ne mogu da pisem pp? [ Bojan Basic @ 21.06.2006. 14:23 ] @
Možeš mi se javiti preko ICQ-a, Jabbera, e-maila (sve ovo ima u mom profilu), a ako se radi o nečemu što možda zanima i ostale članove foruma slobodno postavi temu.
Što se tiče zadatka, da li je lep zavisi od ukusa, ali za IMO definitvno nije, jer se radi o potpuno neoriginalnoj stvari koja se pojavljivala na 1000 različitih mesta. Sam sastavljač zadatka (Jan Wil iz Estonije) kaže da je problem sastavio tako što organizatori estonskog takmičenja nisu umeli da smisle lepe probleme, i onda je rekao: „Vrlo je lako sastaviti probleme, posebno iz kombinatorike. Uzmite proizvoljan oblik (nacrtao je našu kuku na tabli), i zapitajte se da li je moguće njom pokriti pravougaonik!“. Kako sam kaže, nikad nije pomišljao ni da će ovaj problem doći na estonskom nacionalnom takmičenju, a posebno ne na Olimpijadi. To je inače njegov drugi problem na IMO, prvi je bio 1999, zadatak 1. [ useer @ 21.06.2006. 14:34 ] @
pa pitanje je jednostavno i zanimalo bi verovatno sve mladje posto si bio dobar na imo:
da li si u os bio dobar takmicar kao i u srednjoj skoli i da li si bio na jbmo? [ Bojan Basic @ 21.06.2006. 14:50 ] @
Bio sam dosta dobar, a nisam bio na JBMO pošto mi je na Saveznom falilo 1-2 mesta (ne sećam se tačno, davno je bilo), a Malu tada nisu organizovali.
[ useer @ 21.06.2006. 14:55 ] @
ok hvala i jos jedna stvar oni zadaci sto si mi pre neki dan dao na temi "samo trigonometrija" da li imaju elementarno resenje posto mi izgleda da resenje prvog trigonometrijom sigurno ne bih napakovao....
[ Bojan Basic @ 21.06.2006. 15:08 ] @
Imaju, naravno (svaki geometrijski zadatak ima elementarno rešenje samo je pitanje koliko ga je teško naći), ali bih te zamolio da diskusiju o tome nastavimo na http://www.elitesecurity.org/tema/182755 jer se ovde radi o sasvim drugoj temi.
[ useer @ 21.06.2006. 15:22 ] @
uredu..a ako je ovaj ranije pomenuti zadatak vec tako "ruzan" i lak zasto je bio onako slabo resen(bar u nasoj ekipi nissam siguran za ostale)
[ Bojan Basic @ 21.06.2006. 15:34 ] @
Nisam nigde rekao da je lak, samo da nije tip zadatka kakav je poželjan na IMO.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|