Evo ovako, obe f-je su sa minimumom, i to samo jednim. Iz njihovih prvih izvoda mozes da dobijes koordinate njihovih ekstremuma:

,
,

Kod minimuma će važiti:

,
,

Kada vratis ove vrednost x u jednačine, dobićes odgovarajuće vrednosti y. Ovo su koordinate tačaka:

,

Treba izjednačiti samo ordinate, tj. vrednosti y:

kako si dobio to prvo 2x-m i 2x-2?

Pa diferenciras prvu i drugu jednacinu po x i izjednacis sa 0.

Ako još nisi radio izvode, ne ulazim, rešenje se sastoji u tome da nađeš koordinate temena ovih funkcija. Teme svake realne f-je oblika , , će biti u . Kada dobiješ temena, postavi njihove y-koordinate sa dve strane jednačine, kao što je gore urađeno, i dobićeš jednačinu sa jednom nepoznatom: m.

da ne stavljam novu temu odrediti k tako da nule budu vece od 3.... znaci i , ali sta jos??

Ja bih to uradio preko Vijetovih formula, znaci: i

Preko Vijeta kako je Sonec rekao dobija se k>1.

Za k=1.2 rešenja su



Ja bih rešio ovako:

.

.

.

.

.

.

_{[Ovu poruku je menjao SrdjanR271 dana 16.11.2011. u 23:19 GMT+1]}

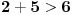
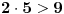
Tacno. Ovaj sistem sto sam postavio je tacan, al ne i dovoljan uslov. Jer ja mogu uzeti brojeve 2,5 kao resenja jednacine, i oni zadovoljavaju resenja sistema, tj. i . A 2 nije vece od 3. Hvala Srdjane na ispravci.

I da, nisam siguran da moze da se uradi kako je @cikin mislio, jer da, teme ce biti vece od 3, al nule funkcije ne moraju biti vece od 3 u tom slucaju (i nisu (tacnije jedna), sem ako je bas teme dvostruka nula, tj. ).
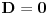