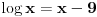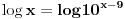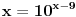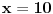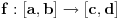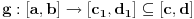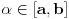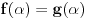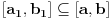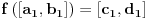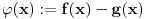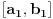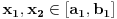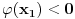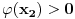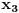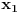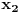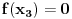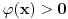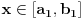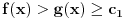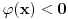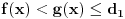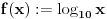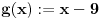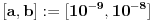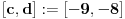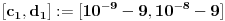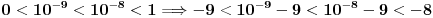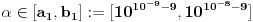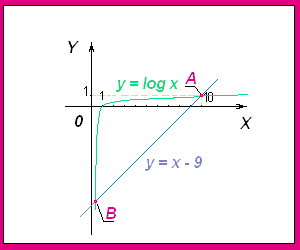Što se samog rešenja tiče:





Znajući da j-na ima samo jedno rešenje (skicirati grafike f-ja), dosta je pronaći jedan broj koji zadovoljava j-nu.


J-na x = log x nema realno rešenje.

Što se opšteg postupka tiče, moraćeš da sačekaš nekog drugog.

Postoji još jedno rešenje - to je geometrijski očigledno, ali da damo i analitički dokaz.


Lema

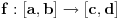
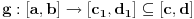
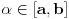
Ako su i neprekidne i surjektivne, onda postoji tačka za koju je .

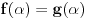
Dokaz.

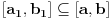
Zbog neprekidnosti f-je mora da postoji barem jedan interval takav da .
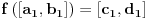
_{Napomena: Na tom intervalu ne mora biti surjektivna. Ako neko želi dokaz postojanja intervala neka traži - pa ću napisati.}

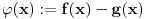
Uvedimo pomoćnu neprekidnu f-ju i posmatrajmo je na intervalu .

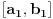
1. Ako ima nulu, lema je dokazana.

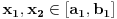
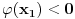
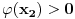
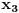
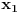
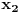
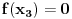
2. Ako nema nulu, onda ne mogu da postoje tačke takve da i , jer bi zbog neprekidnosti postojala i neka tačka između tačaka i za koju bi bilo . Dakle, je konstantnog znaka na .

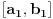
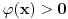
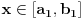
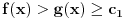
Ako je , onda dobijamo da je za svako što protivreči surjektivnosti f-je .

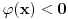
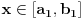
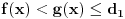
Ako je , onda dobijamo da je za svako što protivreči surjektivnosti f-je .

Dobijene kontradikcije dokazuju postojanje nule.




Sada možemo da primenimo lemu na zadatak.












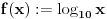
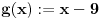
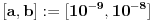
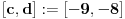
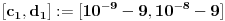
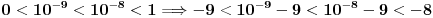
Pa dobijamo da postoji još jedno rešenje .


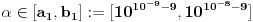
_{[Ovu poruku je menjao uranium dana 28.06.2006. u 03:45 GMT+1]}

Moja greška, tek sada sam pogledao grafik...

Ovakve jednačine se rješavaju numerički.Ima nekoliko
metoda,a najjednostavnija je:"Odreži pa probaj".