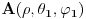
Neka su date različite tačke i .
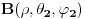
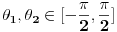
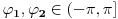
Pri čemu, je radijus, predstavljaju elevaciju a azimut.

Neka je tačka centar sfere.

Sve tačke na duži možemo opisati sa:

, .

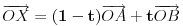
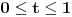
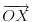
Sada ostaje da vidimo kakvim koeficijentom (u f-ji od ) moramo da pomnožimo vektor da bi dobili tačku na luku (to je moguće, ako )

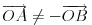
Za početak, znamo da je

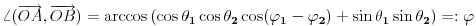_{Ovo je dobijeno prebacivanjem sfernih u Dekartove koordinate a zatim i računanjem skalarnog proizvoda.}

Lako je videti da je

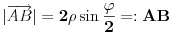
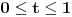
Sada, ako je fiksirano, koristeći kosinusnu teoremu, nalazimo .


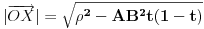
1.

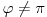
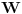
Tačka pripada luku ako i samo ako

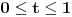
postoji , takvo da


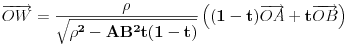
Ostaje da se, eventualno, izvrši razdvajanje po koordinatama a zatim i prevođenje u sferne koordinate...

2.

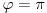
Postoji kontinuum mnogo najkraćih lukova između i ...

Hvala...