Dobro...ima li nekog ko bi bar nesto rekao o rezidijumu uopsteno.
Zelio sam da pitam i sta su to singularne tacke neke funkcije, ali sam nekako shvatio da su to nule funkcije .
Sada jos jedno pitanje. Sta su to polovi funkcije?

Zadatak jos uvijek stoji.

E jbga.. Nemoj se ljutiti, ali kako si mislio rijesiti navedeni integral ako uopce nisi usvojio sam pojam rezidua, stavise niti singulariteta? .. a ko zna kako stojis i s analiticnoscu ili Laurentovim redom..
Zadatak sam rijesio i taman ti ga mislio otipkati, ali nakon ove tvoje druge poruke cini mi se besmislenim trositi vrijeme..

Sto se tice ovoga da trazis da ti neko objasni ovih par pojmova.. tesko da ce ti neko to bolje objasniti nego sto ces naci u svakoj knjizi o komplexnoj analizi.. pa mislim da bi bilo fer od tebe da najprije pokusas to skontati iz knjiga, a ONDA ako bude zapinjalo javi se ovdje s nejasnocama...

Konacno, mislim da bi sljedeca knjiga mogla biti upravo ono sto tebi treba:

1) V. Devide ( i grupa autora), Rijeseni zadaci iz vise matematike, svezak IV, Skolska Knjiga Zagreb 1990.
(Ovu knjigu ti najtoplije preporucujem, jer u njoj su lijepo metodicki od jednostavnijih prema tezim izlozeni POTPUNO RIJESENI zadaci.. a pored toga na pocetkku svake cjeline se nalazi uvod s kratko izlozenim najvaznijim definicijama i teoremima (cini mi se da bi ti volio bas tako nesto). Ako je ne mozes naci kod vas, javi pa ti mogu kopirati i poslati (oko 100 stranica) Vjeruj mi neces pozaliti.)

A inace za teoriju, evo sljedece dvije odlicne knjige:

2) Kurepa, Matematicka analiza IV, Tehnicka knjiga Zagreb
3) Mitrinovic, Komplexna analiza, Gradjevinska knjiga Beograd

Nadam se da se ne ljutis. Pozdrav

:-) Drugim rijecima, ja postavim pitanje...ti mi ne odgovoris vec mi kazes da potrazim odgovor u knjigama koje ne mogu da nadjem, hah. Ne ljutim se, malo mi je simpatican (?) tvoj odgovor ali ajde.
Dakle, mislim da cemo se sloziti kada kazem da nije bas lako shvatiti i prihvatiti matematicke pojmove citajuci onu 1 ili mozda 2 strane, iz neke knjige, koje objasnjavaju (bolje reci pokusavaju) zadatke koji slijede!?
Ja sam rekao vec da nemam neku literaturu i zamolio za pomoc...tako da...ako ne zelis ili ne mozes da pomognes zasto pises? Dakle, nemoj se ni ti ljutiti...ali ja sam samo zelio pomoc (zbog cega svi mi i dolazimo na ovaj forum, zar ne?).
Nadam se da ce bar neko uraditi bar dio zadatka da bih nekako uspio da shvatim nesto, iz zadataka koje sam uradio uspio sam da shvatim dosta o rezidijumima (kako shvatih to su ostaci funkcija?) i ost. ali opet zapinje...

Zahvaljujem.
Pozdrav.



p.s.1 E da...i funkcija je analiticka u nekoj tacki ako je diferencijabilna u istoj tj. ako postoji prvi izvod...jeli tako dodje??

p.s.2 Na tu ponudu nemam sta da kazem osim...mnogo lijepo od tebe. Hvala ipak.

_{[Ovu poruku je menjao MixMaster dana 03.07.2006. u 23:18 GMT+1]}

F-ja je analiticka ako ima neprekidan prvi izvod! Ako ima izvod u nekoj tacki ona je mislim holomorfna.

Tebi verovatno kaze da je x pripada C singularitet f-je f(z) ako f(z) nije analiticka u z=x. Da to znaci da nema izvod u tacki x.

Edit: Jbga, cini mi se da nesto grijesim s tex kodom ako ga ne vidis, ne znam zasto nece da mi ga prikaze..



Uh:)..
Na tvoju zalost i dalje ostajem pri tom da nema smisla pitati takve stvari PRIJE nego se pokusalo uciti ih iz literature. A to sto kazes da nemas ili ne mozes doci do knjiga je, mislim, prije pitanje tvoje "lijenosti" nego stvarnog stanja.. najprije zato sto literatura postoji sigurno u knjiznici na tvom faksu, a ako ne (sto je malo vjerojatno), sigurno mozes pitati profesora ili asistenta.. a u prilog tomu ide i to da ti evo ja nudim da kopiram (o svom trosku, koji doduse i nije velik..) i posaljem fenomenalnu knjigu a ti odbijas..

No, ok, cini se da je to tvoj izbor, tj nacin ucenja i polaganja ispita (trenutno, pismenih) bez citanja knjiga.. i imas pravo na njega, mada je meni neshvatljivo da neko polaze ispit a nema osnovnu literaturu iz toga. (Ok, mozda ti i ne polazes ispit i ovo si pitao tek iz hobija, u tom slucaju se ispricavam na ovim insinuacijama:) )

Nadalje, pitas me zasto pisem ako ne zelim pomoci..
e pa najprije, zelio sam pomoci nakon tvog prvog posta, i rijesio integral misleci da spremas ispit i da si rjesavao zadatke i da si UCIO! ali eto bas ti taj tip integrala (beskonacno u granicama) ne ide.. i taman ti ga, kako rekoh, htio otipkati i objasniti.. ali onda si napisao onaj drugi post u kojem si pitao preelementarne stvari i sugerirao mi da je besmisleno da ti otipkam rjesenje iz jednostavnog razloga - jer se u rjesenju tog integrala PRETPOSTAVLJA poznavanje klasifikacije singulariteta, analiticnost, razvoj u Laurentov red, pa i Cauchy-evi teoremi.. a pogotovo pojam residua i kako se on racuna ovisno o vrsti singulariteta.. a to su sve pojmovi, koje ti, barem prema tvojim postovima, jos nisi usvojio..
Zato sam, umjesto da ti otipkam rjesenje.. koje, ma kako se ja trudio, neces shvatiti bez poznavanja osnovnih pojmova.. sam smatrao da je bolje da te uputim na onu super zbirku rijesenih zadataka, iz razloga koje sam naveo, a pogotovo jer za tu zbirku ne vazi ona istina sto si rekao da se iz dvije stranice teorije kao sto je obicaj u vecini zbirki tesko moze nauciti.. jer ova zbirka je pisana drugacije i blje.. i dokazuje da je ipak moguce.. i ja ti opet savjetujem da pokusas doci do nje..

Sad vjerojatno gundjas u sebi:).. pomalo ljut.. sta ja tu nesto pisem.. pa mi dopusti da ti pokusam oslikati tvoje trazenje, kako bi me bolje razumio..
Naime, ono sto ti trazis, parafrazirano izgleda ovako:
"Molim pomoc u rjesavanju integrala pomocu rezidua u beskonacnim granicama (koji je kruna cijele jednosemestralne komplexne analize (op. a.) i zadnji zadatak na ispitu ).."
i neko ti pocne tipkati rjesenje, ali vidi tvoj drugi post:
".. pri cemu ne znam uopce sto je reziduum (znam da je neki ostatak funkcije, ali nemam pojma sto s tim) niti kako se odredjuje.. ne znam sto je to singularitet, stavise, ne znam uopce da postoji vise vrsta singulariteta i da se ovisno o vrsti drugacije nalazi reziduum.. nadalje, cuo sam da postoji tamo neki "pol" pa molim recite mi sto je to.. a tek da je Laurentov red jedan od nuzijih preduvjeta za nalazenje rezidua, to mi nije palo ni na pamet.."

E sad, usporedi ovo trazenje sa recimo trazenjem jednog srednjoskolca na forumu:
"Molim pomoc u rjesavanju trigonometrijske nejednazdbe s apsolutnim vrijednostima..." i sad mu ti recimo odlucis pomoci i rijesis mu zadatak i pocnes tipkati.. kad vidis novi post:
"Pa zar mi niko nece rijesiti.. a jel moze mi neko reci uopce sto je to sinus, cosinus, tangens?.. I kako se inace rjesavaju nejednadzbe, znam da je to nesto slicno kao i jednadzbe.. I jel ova apsolutna vrijednost isto kao i da pise obicna zagrada?.."
I sto bi mu ti nakon tog drugog posta odgovorio?:)

Eto, molim te i dalje da se ne ljutis nego me pokusas shvatiti da ti u stvari zelim pomoci sugerirajuci ti onu zbirku, ili prethodno citanje iz literature pa tek onda javljanje ovamo s poteskocama, (uostalom takvo je i neko nepisano pravilo na forumima, ljudi ne vole odgovarati na pitanja ako ne osjete da je pitalac ulozio neki trud u trazenju odgovora, pa ipak nije uspio..)

Na kraju, da ne mislis da se tu samo pravim pametnjakovic, evo ti i kratkih i vjerojatno matematicki ne potpuno preciznih ali nadam se razumljivih odgovora na tvoja pitanja, koja nadam se neces razumjeti i ipak ces kao pravi student takve "osnovne" stvari nauciti iz literature, a onda ovamo pitati neke zackoljice i eventualne nejasnoce:) .. :

- komplexna funkcija je analiticka na W podskup C ako je derivabilna u svakoj tocki iz W i ta derivacija je neprekidna na W (tj u svakoj tocki iz W).

- analiticnost, holomorfnost, i regularnost komplexne funkcije mozes smatrati sinonimima

- tocka z0 iz C je izolirani singularitet komplexne funkcije ako postoji okolina od z0 (bez z0) u kojoj je ta funkcija analiticka, ali u tocki z0 ili funkcija nije definirana ili ako je definirana nije u njoj analiticka.

- Ako je z0 izolirani singularitet, tj neka funkcija je analiticka u nekoj njenoj okolini (bez z0), tada se funkcija na toj okolini moze razviti u Laurentov red

- Laurentov red mozes zamisliti kao poopcenje Taylorovog reda u minus beskonacnost.. (nesto "slicno" kao sto je skup Z "poopcenje" skupa N).. tako da mu dodas beskonacno clanova s negativnim eksponentima faktora (z-z0).. Dakle Laurentov red oko tocke z0 izgleda ovako:

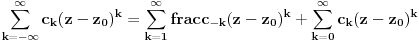
, pri cemu je z iz pomenute okoline (bez z0). Prvih beskonacno sumanada se naziva glavni dio Laurentova razvoja, a drugih beskonacno regularni dio.

- Zasto je taj Laurentov red vazan... zato sto pomocu njega mozemo odrediti vrstu singulariteta tocke z0:
1) Ako su u glavnom dijelu Laurentova razvoja svi koeficijenti jednaki nuli onda je z0 uklonjiv izolirani singularitet.
2) Ako u glavnom dijelu Laurentova razvoja ima konacno mnogo koeficijenata s negativnim indexima, razlicitih od nule, a svi ostali clanovi s negativnim koeficijentima jednaki nula, (tj ako postoji neki prirodan broj m takav da prvih m-clanova s negativnim indexima je razlicito od nule, a svi ostali jednaki nuli) .. tada funkcija u izoliranom singularitetu z0 ima pol m-tog reda
3) Ako glavni dio Laurentova razvoja ima beskonacno clanova, tada funkcija u z0 ima bitan singularitet

-(Pomenute tri vrste singulariteta se mogu definirati i pomocu limesa:
1') analiticka funkcija na nekoj okolini od z0 (bez z0) ima u z0 uklonjiv singularitet akko postoji limesf(z) kad z->z0, i taj limes je naravno iz C (hoce reci da postoji okolina od z0 u kojoj su vrijdnosti funkcije ogranicene)
2') izolirani singularitet z0 od analiticke funkcije je pol od funkcije akko je limes|f(z)|=+beskonacno. (Pol se u praksi najcesce nalazi tako da trazimo nultocke nazivnika.. naravno posto nultocke mogu biti prvog, drugog, treceg, ... n-tog reda, tako ce i pol biti odgovarajuceg reda.)
3') analiticka funkcija ce u z0 imati bitan singularitet akko lim|f(z)| kad z->z0 ne postoji (ni konacan ni beskonacan)

- Kompaktificiramo li prostor C tako da ga zatvorimo s "tockom" beskonacno, tada i beskonacno moze biti izolirani singularitet.. Naravno i on moze biti uklonjiv, pol, ili bitan, ali to objasniti zahtijeva par dodatnih crta objasnjenja koja necu pisati sada.

I naposljetku dolazimo do kljucnog pojma: reziduum komplexne funkcije u izoliranom singularitetu:

- reziduum komplexne funkcije f u izoliranom singularitetu z0 se oznacava s
Res(f;z0), i definira ovako:
Res(f;z0)=,
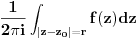
pri cemu je r odabrano tako da je f analiticka na okolini od z0 radijusa p, p>r. (Prema Cauchyevom teoremu (koji necu pisati, ali je takodjer prevazan u cijeloj prici) je jasno da kruznicu |z-z0|=r mozemo zamijeniti bilo kojom pozitivno orijentiranom konturom K sadrzanom u okolino radijusa p).

I sad ono sto tebi treba, tj formula za racunanje integrala pomocu rezidua:

- Ako je funkcija analiticka u nekom podrucju osim u konacno mnogo (npr. m) signularnih tocaka, i K zatvorena krivulja koja obuhvaca te tocke i ne prolazi niti jednom od njih tada je:


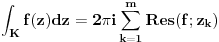
- Preostaje jos pitanje, kako naci te rezidue, jer definiciona jednakost pretpostavlja poznavanje integrala kojeg zapravo mi zelimo izracunati. Za to nam sluzi Laurentov razvoj. Naime:

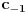
a) reziduum funkcije u tocki z0 (izoliranom singularitetu) nije nista drugo nego koeficijent u Laurentovom razvoju u okolini z0, tj:


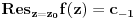
b) ako je f analiticka u okolini "tocke" beskonacno, onda je reziduum:

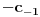
c) ako je z0 uklonjiv singularitet od funkcije, tada je

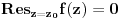
d) ako je z0 pol m-tog reda funkcije f, tada se reziduum racuna ovako:


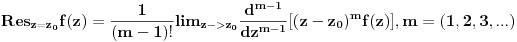
e) ako je z0 bitni singularitet nema jednostavnijeg rjesenja, nego ipak razviti funkciju u Laurentov red i prvi koeficijent s negativnim indexom ce biti reziduum.

Eto.. nadam se da si zadovoljan sto sam izgubio vise od sat vremena tipkajuci ti nesto sto si mogao naci u bilo kojoj knjizi iz komplexne analize..
i nadam se da ti je jasno zasto sam napisao da najprije treba uloziti malo truda i uciti, pa tek onda pitati na forumu.. pogotovo pitanja koja si ti pitao.. jer bi nam svima lakse bilo da si ovo proucio sam i ovdje pitao dio po dio koji ti je nejasan.. a ne da ovdje ljudi pisu skripte za tebe..

pozdrav



_{[Ovu poruku je menjao Mlatko dana 04.07.2006. u 22:15 GMT+1]}

Hm, sta reci na ovakav post. Prije svega, hvala Ajde sada o matematici...
Sto se tice "lenjosti", moram priznati da jesam lijenj...ali stani! Nemoj odmah da odmahnes rukom i da kazes "e to je to"
Sto se tice ovih stvari o kojima pricamo, dakle fakultetu, ucenju i sl. moram ipak reci da se podosta trudim. Zasto? Zato sto me ove stvari interesuju (sto malo ljudi na mom fakult. moze reci za sebe...mislim na ovo "interesovanje").
Inace, studiram ETF i interesuju me malo vise neke druge stvari...npr. elektronika, programiranje i sl. u kojima sam dosta dobar. E sada, kako covjek ne moze biti dobar u svemu (ili mozda moze?) ni meni neki dijelovi matematike ne idu dobro.
U ovom roku sam dosta ucio neke druge stvari i nisam stigao da se vise posvetim kompleksnoj analizi (koja je jedna od 7-8 oblasti koja dolazi na ispitu)...ipak, da bih naucio i to, nasao sam kao vec rekoh knjigu Milicic-Uscumlic 2, koja mi i nije bas pomogla sa svojim objasnjenjima (opet da kazem "kao sto vec rekoh" ).
Ne slazem se u potpunosti sa tvojim poredjenjem, ali moram reci da ove stvari jesu osnovne u kompleksnoj an. kao sto si i rekao...ali bih se opet nadovezao na moju pricu koju sam vec ispricao.

Dakle, nemam razloga da se ljutim, u pravu si...ali stoji, da ja moram kako znam i umijem na naucim kompl. an. Ukoliko tvoja ponuda jos stoji (a kako ja nisam siguran da cu u ovom roku uspjeti da polozim ovu matemat.) prihvatio bih je (moram ti priznati da me je ta ponuda i zacudila malo...jer nema puno ljudi koji bi tako nesto uradili), ali bih zelio ipak da ja platim za kopiranje. Cekam tvoj sledeci post, pa cemo da vidimo...

Poz.

jedna od 7-8 oblasti.. hm..
sorry ja sam (ne znam zasto) otpocetka mislio da ti je cijeli ispit iz komplexne analize (kao sto je recimo na pfm-u, najmanje jedan semestar samo komplexna..)..
Ovo sad objasnjava tvoju "lijenost":) i moje cudjenje.. kako mozes pitati o reziduima a nisi presao singularitete i redove..

Sad vise nisam siguran.. Ona zbirka je stvarno odlicna, ali samo za one koji spremaju ispit koji je cijeli samo komplexna analiza.. U tvom slucaju, tj ako je to samo jedan od pet ili sedam osam tipova zadataka na ispitu, mozda je ipak malo previse.. tj trebao bi izgubiti previse vremena da bi sve pobrao, a na kraju je to samo jedan zadatak na ispitu.. (nama pmf-ovcima je lakse jer svih pet zadataka je iz komplexne, pa zato duze vremena spremamo, detaljnije predjemo i vjerojatno bolje shvatimo..)

Naravno ovo ne govorim zato da izbjegnem kopiranje i slanje zbirke, nego ne bih zelio da se izgubis u zbirci i trosis vrijeme na nesto sto ti ne treba.. a ujedno mi pada na pamet jedna brza i efikasnija ideja:
Ne znam sto vi ucite iz kompl. analize, ali ako vam se javlja samo zadatak iz rezidua na ispitu, onda je mozda najbolje da ti ja skeniram tih desetak stranica koji obradjuju rezidue iz zbirke i posaljem mailom..

I da sad vise ovdje ne uzurpiramo prostor foruma..

Pogledaj u svojim predavanjima koja ste poglavlja kompl analize ucili, i ja cu iz toga izabrati eventualno jos neke dijelove zbirke ili neke druge knjige i skenirati i poslati (ako ih ne bude puno)..
Ako bude mnogo stranica, i ako odlucis to izici neki drugi rok, onda je lakse da iskopiram i posaljem postom.. trosak tu nije vazan.. to je premalo novaca kad se usporedi s onim sto ce nasa civilizacija dobiti tvojim buducim znanjem:)..

Eto pa javi se na mail..

p.s. Nazalost sutra u podne idem na put tri dana, pa ako bas hoces izici ovaj rok, javi barem do devet ujutro..

p.s.2. I javi mi jel ti vidis tex kod koji sam tipkao.. ja ga ne vidim, a stvarno ne znam gdje grijesim..

Poslao sam mail.

Pozdrav

(Opet moram uzurpirati prostor foruma zato sto mi ne dozvoljava da pisem PP i saljem mail jer "nisam registriran barem 2 sedmice.." :) )
A htjedoh ti samo javiti da nisam dobio nikakav mail.
No bez obzira na to maloprije sam pokusao ti ipak skenirati barem reziduume da ih prikacim ovdje, ali skener nece pa nece.. a nazalost uskoro idem na put i nemam vremena sad ga troubleshootirati..

Pozdrav

U redu, sta da se radi... Uspio sam nekako da uradim nekoliko slicnih primjera onog zadatka...
Ti, kada budes imao vremena skeniraj i posalji.

Hvala i pozdrav.