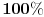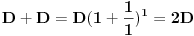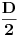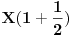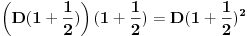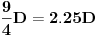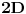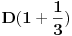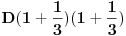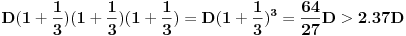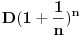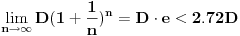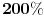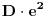Sve se primjenjuje. Svaka oblast matematike je nastala iz potreba koje je imala neka druga nauka.
Ja na faksu kad sam učio specijalne funkcije (Besselove, Gamma, Ermitovi polinomi i sl.) mislio sam da je to najveća glupost koja nikome ne treba. Poslije sam vidio da imaju svoju primjenu.

:)
Hm, da li bi se matematičari složili sa tim?

Možda nama inženjerima izgleda tako, ali sam ipak skloniji da verujem da je matematika u našem vremenu samostalna nauka, a mi ostali samo muzemo, da prostiš, njene proizvode i koristimo gde nam treba. Mislim da je bila tema o ovome na forumu...

Od sve matematike na faxu najružnija mi je bila algebra. Prilično sam se pomučio dok sam je položio, a onda me je ona sačekala na završnoj godini iz predmeta Kodovi za prenos i zapis i na samom diplomskom koji sam uzeo iz kodova. (Tako to najčešće biva u životu) Jedan od udžbenika koje mi je bio referenca za izradu diplomskog je bila: F. J. MacWilliams, N. J. A. Sloane: ''The Theory of Error Correcting Codes''. Kakva je to suva algebra bila, a ja mislio da sam dostigao plafon sa kursom algebre na prvoj godini! Eto jedne primene algebre u teriji kodiranja, a gde se sve kodiranje primenjuje valjda ne moram ni da pišem.

_{[Ovu poruku je menjao darkon dana 06.07.2006. u 13:17 GMT+1]}

Ne mogu da odolim

Bart: Neverovatno Liza, ali ti si nasla prakticnu primenu geometrije.

Mislim da matematika nije sama sebi svrha. Iz potrebe naučnika da riješe neki problem razvije se određeni matematički aparat. Npr. diferencijalni račun je nastao iz potrebe da se izračuna brzina nekog tijela na osnovu putanje ili iz potrebe da se odredi jednačina tangente na krivu. Integralni račun je nastao iz potrebe da se npr. odredi rad, ako je poznata promjena snage u vremenu ili da se izračuna površina ispod neke krive. Iako, "određivanje jednačine tangente" ili "površine ispod krive" djeluju kao čisto matematički problemi to su ustvari praktični problemi. Poslije matematičari generalizuju stvari (npr. n-dimenzionalni vektorski prostori i sl.) koji nemaju praktičnu primjenu, ali su korisni za razumijevanje problema.
Tako da mislim da svaka oblast ima praktičnu naučnu primjenu. U suprotnom bi većina matematičkih oblasti bila čista enigmatika. ;)

Kao što već rekoh, na sličnu temu je već raspravljano na ovom forumu.
Pogledaj npr.
http://www.elitesecurity.org/p314542
a nije loše pročitati kompletnu temu da se ne bismo ovde ponavljali.


Ne bih se složio sa ovim. Opet navodim kodove kao primer.

Optimizacija je jedna od korisnijih primenjenih matematika, a u njoj se koristi sve i svašta iz matematike, čak i ono pto se na prvi pogled ni ne bi moglo nazvati matematikom (npr. genetski algoritmi). Dijkstra je bio legenda i programiranja i matematike u oblasti optimizacije.

Jedan od najstarijih sačuvanih egipatskih zadataka (u obliku pesmice):



_{Citat je iz knjige Kratak pregled istorije matematike, Dirk J. Struik}


Jedan primer iz knjige Papagajeva teorema, Denis Guedj:

Zamislimo da želimo da uložimo dinara u banku.
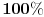
Bankar nam nudi (jednostavnosti radi) kamatu od na godinu dana.

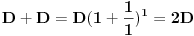
Dakle, ako bi uložili din. na godinu dana, pri tolikoj kamati, nakon isteka tih godinu dana imali bismo dinara (bilo bi nam vraćeno koliko smo uložili, i još kamata na taj iznos).

Nešto nam padne na pamet...šta ako bismo uloženi novac povukli posle pola godine...pa ga odmah ponovo uložili na preostalih pola godine?
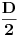
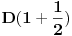
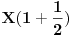
Dakle, na polovini godine, bi nam bilo vraćeno ono što smo uložili tj. dinara i još polovina obećanog iznosa na ime kamate tj. znači, ukupno dinara - odmah primetimo zakonitost - ako pri istim uslovima, uloženih dinara povučemo na polovini roka, dobićemo dinara.
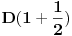
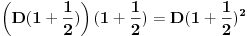
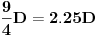
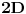
Znajući to, uložimo onih dinara na preostalih pola godine - pa tako na kraju godine imamo . Primećujemo da bismo na taj način dobili , a to je bolje nego onih dobijenih nakon god. dana bez uzimanja i vraćanja.

A šta bi se desilo ako bismo istu stvar uradili na 1. i 2. trećini godine?

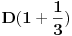
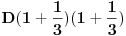
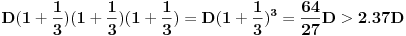
Posle prve trećine imali bismo dinara - sve to uložimo ponovo - pa posle druge trećine imamo - sve to uložimo ponovo - pa na kraju godine imamo što je opet bolje nego prethodno.

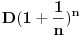
Dakle, ako bismo mogli da uradimo ovo puta u toku godine na kraju bismo imali dinara. Očigledno, u interesu nam je da bude što veće - pa nam pada na pamet da izračunamo .

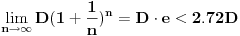
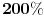
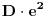
Da je kamata bila npr. u idealnom slučaju "uzeli" bi dinara...

_{Molio bih ekonomiste da zaobiđu ovaj primer}

Koja druga nauka je dovela do pojave Teorije dokaza (da nisu pravne nauke? ), Teorije modela, Teorije skupova, Teorije Galoa...?

Naravno da ima i mat. teorija koje su nastale isključivo zahvaljujući nekim praktičnim primenama (npr. Teorija informacija), ali sam ubeđen da primenljivost mat. otrkića van matematike igra beznačajnu ulogu u smislu profesionalne motivacije istraživačima (naravno, kad treba izboriti novac za "projekte", putovanja i usavršavanja svi će se truditi da da dokažu suprotno ). Ako bi to bilo drugačije, bili bismo zatrpani revolucionarnim matematičkim radovima inženjera - koji eto jednom nogom stoje u teoriji a drugom u praksi (koja bi trebalo da je neiscrpan izvor inspiracije).

Konačno, dolazimo do toga da izgleda ne pokreću iste (psihološke) sile matematičare i npr. inženjere te da ni njihove ambicije nisu iste...

Univerzalna algebra je nasla primenu u informatici. A Matematicke analize, linearna algebra, geometrije... u fizici. Ali takodje matematika nalazi svoju primenu i u ekonomiji John Nash matematicar koji je dodio Nobelovu nagradu za ekonomiju 1994. Po njemu je snimljen "Beautiful mind". Naravno za matematiku ne postoji Nobelova nagrada :( Ali kolko je meni poznato postoji Abelova nagrada za matematiku i mozda se tu posmatra samo matematika bez nekih vecih primena. Po meni bi bila mnogo jaca rasprava koje oblasti matematike se ne primenjuju nigde?

Apsolutno se slažem, jer mnogo teže je pitanje gdje se matematika ne primjenjuje!

Problem je što su ljudi "slijepi" za prijemene matematike u svakodnevnom životu, te nekako "intuitivno" zaključuju da matematike "nema nigdje"!

I ja se slazem da bi bilo bolje raspravljati koja se grana matematike nigde ne koristi.
Ja sam uvek nekako najvise mrzeo algebru, narocito omrazenu teoriju grupa za koju ni dan danas ne znam cemu sluzi... bljak...

Mislim da će ti posle ovog citata biti jasnije:




Group theory

Kao što se vidi sa linka koji je dao darkon, neka teorija može da se primenjuje, a da to nije baš očigledno (tj. direktno). Osim toga, ako nešto trenutno i nema primenu, ona se može i treba naći, jer ako je ljudski um bio sposoban da to stvori, biće dovoljno sposoban i da nađe primenu.

Čini se da je koren svakog istraživanja u matematici upravo problem iz realnog sveta - njegovo modelovanje i rešavanje. Kako vreme teče pojaviće se potreba za rešavanje problema u okviru problema, i tako u nedogled... Otuda u nekim granama matematike nema jasne veze sa realnim svetom zato što je radom ljudi u veoma dugom vremenskom periodu skupljeno iskustva koje je plodno ili neplodno uticalo na problem, a veoma često izrodilo nove probleme ili ideje za rešavanje postojećih u istoj ili drugoj oblasti. Govorim o pojavi sličnoj fisiji. Za granu matematike i istraživanje u njoj glavni faktori su snaga zajednice ljudi koji istražuju i realna potreba za tim u industriji, nauci,...
Algebra je dosta često na tapetu, ali je upravo ona izrodila metode koje garantuju ispravnost mnogih metoda za rešavanje problema u jakoj sprezi sa logikom naravno.

Da nabacam par stvari:

U ekonomiji deterministicki haos. Veza inflacije i kamatnih stopa.
Na delu se to pokazalo u nekoj latinoamerickoj zemlji.
Kad sam bio druga godina faxa utruipovao sam da complexni brojevi ne sluzi nicemu i nikome.
A onda mi je jedan elektronac rekao da bez njih osnovne stvari bi resavali mnogosturko duze i teze.

Moj primer iz mladosti.
Htedoh da napravim od papira ( kvadratnog oblika ) kutiju sto vece zapremine.
Dobio sam kvadratnu fuknciju, pa onda prvi ozvod, nule f-je, ...


Malko off-topic, ali matematika nastoji da bude sto je moguce apstraktnija.
Cist i najcistiji alat. A to na sta ce neko da upotrebi to je vec njegova stvar i druga prica.

Teorija grupa je nasla primenu u fizici. Grupe permutacija nasle su primenu u fizici kristala u istoj mislim da imaju primenu i dijedarske grupe, svima nam je poznata Lorentzova grupa (preko nje je Lorentz dosao do istoimenih transformacija). A ako uzmes Kurepinu visu Algebru videces njegove primere sijaset grupa koje se primenjuju u fizici.
Nema oblasti matematike koja nema primenu.

Lepog li materijala za neki rad covek samo treba da uradi copy paste i malo sredi fontove ...