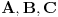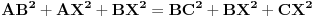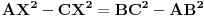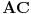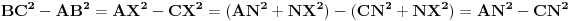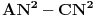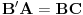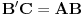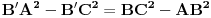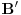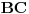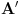[ useer @ 08.07.2006. 14:43 ] @
| ovaj zadatak je valjda bio neki predlog za IMO 1997,ali ja nigde na netu nisam nasao resenje.. A i zadatak mi deluje lep,pa ako neko ima vremena neka ga uradi i pokaze ovde Zadatak glasi: Neka su A,B i C tri nekolinearne tacke.Dokazati da postoji tacno jedna tacka X u ravni ABC tako da vazi: AB^2+AX^2+BX^2=BC^2+BX^2+CX^2=AC^2+AX^2+CX^2 |