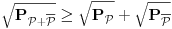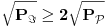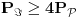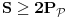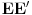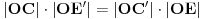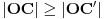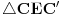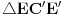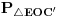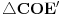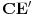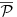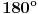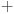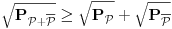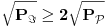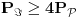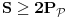Zadaci i zvanična rešenja okačena su uz ovu poruku.
Pošto vidim da je 6. zadatak izazvao mnogo komentara, iskoristio bih priliku da kažem reč-dve o njemu. Zvanična rešenja su previše dugačka i komplikovana (posebno drugo), a zadatak se može rešiti i znatno kraće (i lepše), i to na dva načina.
Prvo nezvanično rešenje:

Kroz svako teme poligona povucimo pravu koja deli njegovu površinu na dva jednaka dela kao na slici. Tačke preseka ovih pravih sa stranicama našeg poligona smatramo temenima novog poligona (to što su uglovi kod tih temena opruženi nema nikakve veze) za koji očigledno važi sve što i za polazni. Nazovimo mašnama figure koje dobijamo u preseku poligona i oblasti oštrih uglova koje čine dve susedne prave — jedna od takvih figura na slici je obojena ljubičastom bojom. Posmatrajmo sada mašnu označenu na slici (isto naravno važi i za sve ostale). Kako prave

i
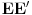
dele površinu poligona na dva jednaka dela, sledi da je

. Iz toga sledi
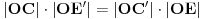
a iz toga, dalje, možemo zaključiti da je ili
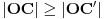
ili

. Dakle, površina ili
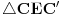
ili
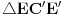
veća je od dvostruke
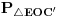
. Slično je i za
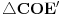
. Dakle, suma površina trouglova koji odgovaraju stranicama

i
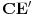
jednaka je bar dvostrukoj površini mašne. Budući da se može lako dokazati da unija svih mašni pokriva ceo poligon, ovim je zadatak rešen.
Ako vam se ovo dopalo, pre nego što pohitam na sledeće rešenje (koje je, bar po mom mišljenju, čak i lepše od ovog) moram da napomenem da koristi malo više matematike tako da nisam siguran koliko će ga svi moći ispratiti. Ipak, potrudio sam se da napravim precizne ilustracije a i, kao i uvek, raspoložen sam da otklonim svaku eventualnu nejasnoću i vrlo rado ću odgovarati na pitanja.
Drugo nezvanično rešenje:

Označimo sa

sumu površina trouglova o kojima je u zadatku reč. Neka je

dati poligon i neka je
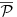
poligon koji se dobija rotacijom za
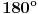
oko neke tačke. Neka je

, gde je znakom
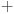
označena suma Minkovskog. Pošto se suma Minkovskog dva poligona može dobiti ređanjem njihovih stranica nekim redosledom, pri čemu je širina dobijene figure po nekom pravcu jednaka zbiru širina polaznih figura po tom pravcu, lako zaključujemo da je

. Kome nije jasno šta sam rekao u prvom delu prethodne rečenice možda će mu slika pomoći — bojama sam pokazao kako se svaki od trouglova pridruženih stranicama početnog mnogougla pojavljuje po dva puta u poligonu
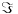
. Preostaje nam samo da iskoristimo dvodimenzionalnu verziju nejednakosti Bruna i Minkovskog (
Brunn-Minkowski Inequality) na figure

i
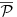
. Zaista: