[ lina @ 17.07.2006. 12:55 ] @
| Mislim da je ovo gimnazijski nivo, ne secam se kada smo ovo radili al bih da se podsetim. x+2y-7<0 -3x+4y+21>0 x>3 (umesto >, treba da bude manje ili jednako i vice versa al ne znam kako se to kuca na tastaturi:))) |
|
[ lina @ 17.07.2006. 12:55 ] @
[ uranium @ 17.07.2006. 14:16 ] @
U ovom slučaju, najlakše je upotrebiti geometrijski metod, tj. svakoj nejednačini pridružimo odgovarajuću jednačinu:
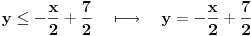   pridružene jednačine određuju odgovarajuće prave u ravni, pa shodno tome, polazne nejednačine određuju odgovarajuće poluravni. Npr. nejednačina 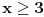 određuje poluravan "desno" od prave određuje poluravan "desno" od prave 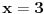 , nejednačina , nejednačina 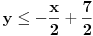 određuje poluravan "ispod" prave određuje poluravan "ispod" prave 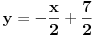 itd. itd. Dakle, rešenje je skup svih tačaka 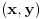 koje se nalaze u preseku svih (nejednačinama opisanih) poluravni. koje se nalaze u preseku svih (nejednačinama opisanih) poluravni.pogledati sliku u prilogu Kada je broj nepoznatih veći od 2, obično se primenjuje Fourier-Motzkin metod... [Ovu poruku je menjao uranium dana 19.07.2006. u 00:46 GMT+1] [ Nedeljko @ 18.07.2006. 21:58 ] @
Rešiti sistem relacija znači odrediti skup svih njegovih rešenja. Furije-Mockinov metod se koristi za ispitivanje da li sistem linearnih jednačina i nejednačina ima barem jedno rešenje ili nema rešenja.
[ uranium @ 19.07.2006. 00:39 ] @
Hm... možda imamo neki nesporazum oko toga šta smatramo rešenim oblikom sistema.
Evo da rešim dati sistem Fourier-Motzkin metodom: 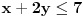 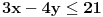 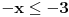 Primera radi, eliminisaćemo  . Dakle, množimo prvu nejednačinu sa 2 i dodajemo drugoj. . Dakle, množimo prvu nejednačinu sa 2 i dodajemo drugoj.Dobijamo redukovan sistem: 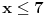 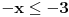 eliminišemo  : :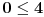 što je tačno, pa možemo da nastavimo vraćanjem unazad... rešavanjem prethodnih redukovanih sistema po odgovarajućim nepoznatim veličinama: 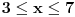 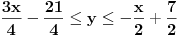 tim uslovima su opisana sva rešenja. Dakle, koliko je meni poznato, Fourier-Motzkin metodom možemo ili da rešimo sistem nejednačina (svođenjem sistema na neki ekvivalentan sistem u rešenom obliku) ili da u nekom trenutku zaključimo da je sistem protivrečan. Druga je stvar to što se lako može konstruisati slučaj u kome je rešen oblik toliko složen da možemo samo da plačemo od muke... [Ovu poruku je menjao uranium dana 19.07.2006. u 20:40 GMT+1] [ THEPRODIGY @ 24.07.2006. 14:26 ] @
Citat: uranium: što je tačno, pa možemo da nastavimo vraćanjem unazad... rešavanjem prethodnih redukovanih sistema po odgovarajućim nepoznatim veličinama: 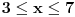 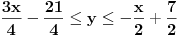 tim uslovima su opisana sva rešenja. ovaj deo ne razumem! sada upisujem prvi razred 6. beogradske! [ uranium @ 24.07.2006. 15:26 ] @
@THEPRODIGY:
Primer koji sam uradio je isuviše jednostavan da bi se jasno pokazali svi detalji Fourier-Motzkin algoritma. Moj prethodni post je bio upućen Nedeljku, pa nije ni bilo potrebe da ulazim u opis postupka, jer on to sve zna, a ako te zanima tačna formulacija algoritma, dokaz da je korektan i tome slično, možeš da pogledaš neku literaturu iz linearnog programiranja... Nisam siguran šta ti nije jasno. Nadam se da vidiš da je: 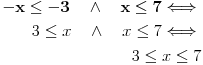 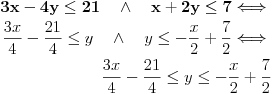 Na kraju, rešenje je skup svih uređenih parova 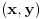 koji zadovoljavaju oba uslova: koji zadovoljavaju oba uslova: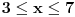 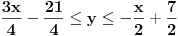 što opet ima očiglednu geometrijsku interpretaciju: u pojasu između trojke i sedmice šetamo se između zadatih pravih. [Ovu poruku je menjao uranium dana 24.07.2006. u 16:49 GMT+1] [ THEPRODIGY @ 24.07.2006. 21:08 ] @
shvatio u potpunosti!
[ Nedeljko @ 25.07.2006. 16:03 ] @
@uranium
Kako misliš da "eliminišeš" promenljivu od čije vrednosti bitno zavisi da li je sistem relacija zadovoljen ili ne (recimo, relacija R(x) je zadovoljena za x=2, a nije zadovoljena za x=3). Da li uopšte znaš šta je eliminacija promenljivih? Ja znam da se na Matematičkom fakultetu u Beogradu eliminacija parametara radi bez ikakvog razumevanja, jer više od 90% profesora pomenutog fakulteta i ne zna šta je to, već samo pljuje po matematičkoj logici. Možeš da pitaš Žarka Mijajlovića ili bilo kog logičara šta je to. Svi ostali će samo da te zavlače. Te, to ti je kad nešto uradiš da se izgubi taj parametar, te ne znam ni ja. Neka je dat sistem relacija R(x,y,t) : x=cos(t), y=sin(t), x,y,t su realni brojevi. Eliminacijom parametra t dobijamo relaciju S(x,y) : x2+y2=1. Postavlja se pitanje u kojoj su logičkoj vezi te dve relacije. Da li možemo kvadrate zameniti kubovima? Zašto baš ta jednačina, a ne neka druga? Veza je sledeća: 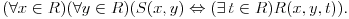 Na žalost, u Beogradu se još ne zna za ovo "otkriće". Dakle, ne radi se tu o ekvivalentnim sistemima relacija. Furije-Mockinov algoritam je algoritam za eliminaciju željene promenljive iz sistema linearnih jednačina i nejednačina, a ne za rešavanje. Ti si ovde samo jedan sistem relacija preveo u neki drugi oblik o kome bi se koglo raspravljati da li je jednostavniji od polaznog. [ uranium @ 26.07.2006. 18:49 ] @
Citat: Nedeljko: @uranium Kako misliš da "eliminišeš" promenljivu od čije vrednosti bitno zavisi da li je sistem relacija zadovoljen ili ne (recimo, relacija R(x) je zadovoljena za x=2, a nije zadovoljena za x=3). Da li uopšte znaš šta je eliminacija promenljivih? Pa i sam si u prethodnom postu napisao da FME (Fourier-Motzkin eliminacija) može da nam odgovori na pitanje zadovoljivosti datog sistema lin. ne/jednačina. Kako misliš da nam to odgovori a da ne saznamo tako elementarnu stvar kao što je opseg dozvoljenih vrednosti te navedene nepoznate  ? ?Citat: Nedeljko: Ja znam da se na Matematičkom fakultetu u Beogradu eliminacija parametara radi bez ikakvog razumevanja, jer više od 90% profesora pomenutog fakulteta i ne zna šta je to, već samo pljuje po matematičkoj logici. Možeš da pitaš Žarka Mijajlovića ili bilo kog logičara šta je to. Svi ostali će samo da te zavlače. Te, to ti je kad nešto uradiš da se izgubi taj parametar, te ne znam ni ja. napisao si neke mnogo zanimljive stvari, ali bojim se da ću otići u OT ako krenem da ih komentarišem Ako si želeo da me oslobodiš odgovornosti za (eventualnu) zabludu u kojoj se nalazim - hvala ti - međutim, potrudiću se u nastavku da pokažem da nisam u zabludi Pošto se iz onog što si napisao može zaključiti da se tvoje i Žarkovo mišljenje o eliminaciji podudara (a budući da si i ti logičar) mogu da zamolim tebe da prokomentarišeš moje viđenje eliminacije. Neka je, primera radi, zadat sistem relacija 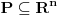 u f-ji promenljivih u f-ji promenljivih 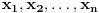 i neka nam pođe za rukom da nekim transformacijama dobijemo neka ograničenja za promenljivu i neka nam pođe za rukom da nekim transformacijama dobijemo neka ograničenja za promenljivu  npr. npr. 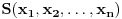 koja su ekvivalentna sistemu relacija koja su ekvivalentna sistemu relacija 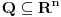 u f-ji promenljivih u f-ji promenljivih  (u kojem se (u kojem se  ne pojavljuje eksplicitno). Na osnovu konstrukcije sistema ne pojavljuje eksplicitno). Na osnovu konstrukcije sistema  jasno je da mora biti jasno je da mora biti 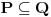 . Ako sada rešimo novi sistem (a to bi trebalo da bude lakše) možemo da se sa tim novootkrivenim vezama između promenljivih . Ako sada rešimo novi sistem (a to bi trebalo da bude lakše) možemo da se sa tim novootkrivenim vezama između promenljivih  vratimo u vratimo u 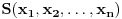 a ako je moguće i u originalni sistem i pokušamo da pronađemo eventualno još neka ograničenja za promenljivu a ako je moguće i u originalni sistem i pokušamo da pronađemo eventualno još neka ograničenja za promenljivu  . U opštem slučaju, sistemi . U opštem slučaju, sistemi  i i  ne moraju biti ekvivalentni, ali ako pričamo o FME pokazaću kasnije da sistemi jesu ekvivalentni. ne moraju biti ekvivalentni, ali ako pričamo o FME pokazaću kasnije da sistemi jesu ekvivalentni. Još nešto, sistem od  linearnih nejednačina sa linearnih nejednačina sa  nepoznatih zapisan na standardan način je u stvari zamena za nepoznatih zapisan na standardan način je u stvari zamena za 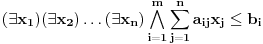 Svaka eliminacija promenljive recimo  (u FME) iz npr. (u FME) iz npr.  -te i -te i  -te nejednačine zapravo ima oblik -te nejednačine zapravo ima oblik 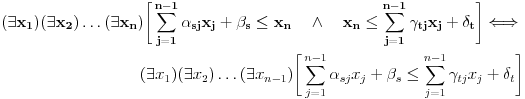 i kad god piše ovo poslednje, podrazumevamo da tu u stvari piše ono prvo. Citat: Nedeljko: Dakle, ne radi se tu o ekvivalentnim sistemima relacija. Furije-Mockinov algoritam je algoritam za eliminaciju željene promenljive iz sistema linearnih jednačina i nejednačina, a ne za rešavanje. Pa ovo me navodi na zaključak da je ono što ti smatraš FME zapravo samo "prvo poluvreme" onog što ja smatram FME. Tako da mi ne gine kucanje... Fourier-Motzkin algoritam eliminacije preuzeto iz Linear Programming, 1: Introduction - George B. Dantzig, Mukund N. Thapa Obeležimo dati sistem nejednačina sa  , započnimo proces stavljajući , započnimo proces stavljajući 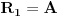 i i 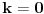 . .1. Postavi 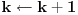 . Ako je . Ako je 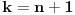 idi na korak 7. idi na korak 7.2. Nejednačine iz 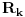 zapiši tako da se promenljiva zapiši tako da se promenljiva 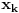 pojavljuje sa koeficijentom pojavljuje sa koeficijentom  , ,  ili ili  na samo jednoj (recimo levoj) strani nejednačine a da sve nejednačine pri tom budu zapisane sa relacijom na samo jednoj (recimo levoj) strani nejednačine a da sve nejednačine pri tom budu zapisane sa relacijom 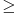 . Sve uslove u kojima je koeficijent uz . Sve uslove u kojima je koeficijent uz 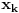 jednak jednak  smatraj delom redukovanog sistema. smatraj delom redukovanog sistema.3. Ako su svi koeficijenti uz 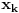 jednaki jednaki  , označi promenljivu , označi promenljivu 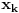 kao proizvoljnu, postavi kao proizvoljnu, postavi 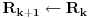 i idi na korak 1. i idi na korak 1.4. Ako su svi koeficijenti uz 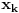 jednaki jednaki  (ili (ili  ), onda: ), onda: {Ako je 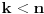 proglasi proglasi 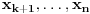 za proizvoljne. Idi na korak 9.} za proizvoljne. Idi na korak 9.}5. Ako su svi koeficijenti uz 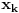 mešavina mešavina  i i  (ili su svi mešavina (ili su svi mešavina  i i  ), onda: ), onda:Uslove sa koeficijentima  proglasi redukovanim sistemom proglasi redukovanim sistemom 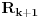 i idi na korak 1. i idi na korak 1.6. Ako postoji makar jedan par nejednačina sa koeficijentima  i i  uz promenljivu uz promenljivu 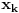 , onda: Za svaki takav par, dodaj redukovanom sistemu njihov zbir. Postavi , onda: Za svaki takav par, dodaj redukovanom sistemu njihov zbir. Postavi 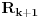 da je redukovani sistem i idi na korak 1. da je redukovani sistem i idi na korak 1.7. Provera neprotivrečnosti. Proveri desne strane sistema 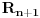 . Ako je barem jedna vrednost pozitivna - proglasi polazni sistem protivrečnim i stani. U protivnom, postavi . Ako je barem jedna vrednost pozitivna - proglasi polazni sistem protivrečnim i stani. U protivnom, postavi  . .8. Određivanje  . Ako je . Ako je 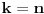 , odredi , odredi  na osnovu na osnovu 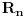 . Postavi . Postavi 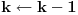 . .9. Smenjivanje unazad. Počni sa 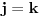 . Dok je god . Dok je god 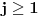 radi sledeće: radi sledeće: a) Ako 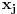 nije označeno kao proizvoljno i ako je nije označeno kao proizvoljno i ako je 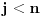 vrati vrati  u u 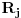 i odredi i odredi 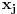 b) Postavi 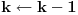 Pozabavimo se sada ekvivalentnošću. Jednostavnosti radi, razmatraćemo šta se dešava pri eliminaciji promenljive  . .Sistem 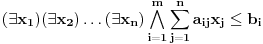 možemo da (nakon sređivanja i izostavljanja kvantora radi sažetosti) podelimo u tri klase: možemo da (nakon sređivanja i izostavljanja kvantora radi sažetosti) podelimo u tri klase: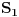 : : 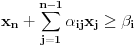 , , 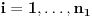 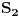 : : 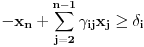 , , 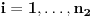 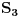 : : 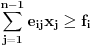 , , 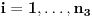 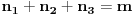 Za početak, zanimljiv je slučaj kada je 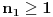 i i 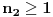 . .Uparivanjem nejednačina iz 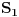 sa nejednačinama iz sa nejednačinama iz 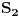 dobijamo sistem od dobijamo sistem od  nejednačina u kojima se nejednačina u kojima se  ne pojavaljuje eksplicitno. ne pojavaljuje eksplicitno.Kao što je ranije objašnjeno, svako rešenje originalnog sistema mora biti rešenje i ovog novodobijenog. Važi i obrnuto. Za svaki par 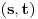 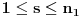 , , 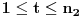 eliminacijom promenljive eliminacijom promenljive  iz iz  -te i -te i  -te nejednačine (iz odgovarajućih klasa) dobijemo: -te nejednačine (iz odgovarajućih klasa) dobijemo: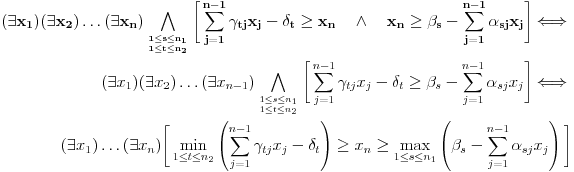 Time je pokazano da je svako rešenje redukovanog sistema ujedno i rešenje originalnog sistema. Citat: Nedeljko: Ti si ovde samo jedan sistem relacija preveo u neki drugi oblik o kome bi se koglo raspravljati da li je jednostavniji od polaznog. Sa ovim se u potpunosti slažem. Smemo li se uopšte nadati da je moguće naći neku "jednostavnu" reprezentaciju rešenja? Na kraju, svako ko je spreman da "proguta" npr. 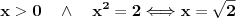 ne bi trebalo da ima bilo šta protiv onakvog oblika rešenja sis. lin. nej. jer je tamo situacija daleko čistija. ne bi trebalo da ima bilo šta protiv onakvog oblika rešenja sis. lin. nej. jer je tamo situacija daleko čistija.[Ovu poruku je menjao uranium dana 26.07.2006. u 20:33 GMT+1] [ Nedeljko @ 29.07.2006. 18:07 ] @
Citat: uranium: Neka je, primera radi, yadat sistem relacija P po promenljivim...i neka nam podje za rukom da nekim transformacijama dobijemo neka ograničenja za promenljivu xn npr. S(x1,...,xn) koja su ekvivalentna sistemu relacija Q Ja ovde ništa ne razumem. Pojasni mi to i potrudi se da budeš maksimalno precizan. [ uranium @ 29.07.2006. 22:41 ] @
Ako pričamo o eliminaciji promenljive u kontekstu FME evo još jednom:
Neka je dat sistem  . . Recimo da želimo da eliminišemo promenljivu  . .Originalni sistem linearnih nejednačina dovedemo u ekvivalentan oblik 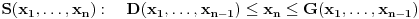 za neke za neke 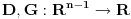 . .Sada imamo redukovan sistem 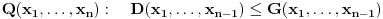 u kome se promenljiva u kome se promenljiva  ne pojavljuje eksplicitno, a to nam olakšava traženje rešenja. Naglasimo i to da je promenljiva ne pojavljuje eksplicitno, a to nam olakšava traženje rešenja. Naglasimo i to da je promenljiva  potpuno određena promenljivama potpuno određena promenljivama 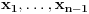 . Dakle, ako bismo hteli da "teramo mak na konac", redukovan sistem bi mogli da pišemo kao . Dakle, ako bismo hteli da "teramo mak na konac", redukovan sistem bi mogli da pišemo kao 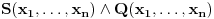 , ali to se ionako podrazumeva. , ali to se ionako podrazumeva.U prethodnoj poruci sam detaljno objasnio da će u slučaju FME biti 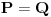 . .Naravno, ovo nije jedini način da se to formalno opiše (ja vidim bar još dve varijante). Sistem nejednačina je shvaćen kao relacija. Relacija se obično poistovećuje sa skupom svih objekata koji je zadovoljavaju. Ja se nadam da si u celosti pročitao moj prethodni post, pa ako i dalje vidiš neku grešku u vezi sa FME - molim te napiši precizno o čemu se radi. Ako imaš da napišeš nešto uopšteno o eliminaciji bilo bi mi zadovoljstvo da to pročitam. [ Nedeljko @ 29.07.2006. 22:49 ] @
Citat: Zapravo, jednoznačno je određen skup svih mogućih vrednosti za xn. No, u prethodnom postu si u delu koji sam citirao ipak govorio uopšteno o eliminaciji parametara. Ovo sada jeste čisto, ali je ograničeno samo na slučaj Furije-Mockinovog algoritma. No, čak i u tom slučaju tome treba da prethodi neka opštija priča. Džaba nam algoritam ako ne znamo šta taj algoritam tačno radi, to jest, šta mu je ulaz, a šta izlaz. [ uranium @ 29.07.2006. 22:54 ] @
Slažem se i zahvaljujem se na ispravci.
Da li možeš da mi preporučiš nešto za čitanje o toj opštoj priči? [ Nedeljko @ 30.07.2006. 11:45 ] @
Pa, sama definicija je jednostavna. Data je relacija R(x1,...,xn,t). Eliminisati parametar t znači naći potrebne i dovoljne uslove po x1,...,xn takve da relacija R(x1,...,xn,t) ima barem jedno rešenje po t. E sad, ako te zanima nešto više o eliminaciji kvantora, ima teorija koje je dopuštaju u opštem slučaju, kao i onih drugih. Tu naravno da ima tomova i tomova knjiga, ali evo nekih teorija koje dopuštaju QE.
- Teorija uređenih realno zatvorenih polja (sledstveno, elementarna euklidska/hiperbolička/projektivna/eliptička/afina geometrija). - Teorija algebarski zatvorenih polja. - Teorija algebarski zatvorenih polja date karakteristike. - Teorija diferencijalno zatvorenih polja. - Teorija gustih linearnih uređenja sa krajevima/bez krajeva/sa levim krajem bez desnog/sa desnim krajem bez levog. - Teorija struktura (R,+,<), (Q,+,<) (ista je). Zanimljivo je da teorija strukture (R,+,*,0,1,<,exp), gde je exp unaran funkcijski znak za eksponencijalnu funkciju, dopušta QE, ali se ne zna da li je odlučiva. Čak i kada neka teorija ne dopušta QE u opštem slučaju, to ne znači da nema važnih posebnih slučajeva QE u njoj. Recimo, teorija algebarskih polja ne dopušta QE u opštem slučaju, ali zato znamo kada kvadratan sistem linearnih jednačina nad poljem ima tačno jedno rešenje - upravo onda kada mu je determinanta različita od nule. [ uranium @ 30.07.2006. 20:10 ] @
@Nedeljko:
...and thanks for all the fish O eliminaciji kvantora zaista postoji brdo literature (što i ne čudi obzirom na značaj tehnike) a o eliminaciji promenljivih jedino što sam našao su radovi iz tzv. Teorije Eliminacije koja se izgleda bavi eliminacijom promenljivih iz sistema polinoma (više promenljivih) a sve to za račun algebarske geometrije... Čisto radi ilustracije, u prilogu je postavljen uvodni odeljak iz doktorske teze Efficient Variable Elimination using Resultants,T. Saxena. Hvala još jednom. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|