[ Djomloun @ 21.07.2006. 18:52 ] @
| Da se ne ponavljam, pitanje je u subjectu, u cemu je razlika(slicnost) ? |
|
[ Djomloun @ 21.07.2006. 18:52 ] @
[ Djomloun @ 22.07.2006. 10:44 ] @
Ajde bwe sigurno neko zna, basx mi treba za ispit.
[ uranium @ 22.07.2006. 12:34 ] @
Neka je
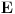 normiran vektorski prostor i neka je normiran vektorski prostor i neka je 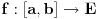 . Ako je . Ako je  podela intervala podela intervala 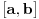 na na  delova tačkama delova tačkama 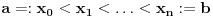 , onda je varijacija f-je , onda je varijacija f-je  po podeli po podeli  : :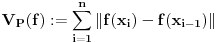 a varijacija f-je  na intervalu na intervalu 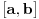 : :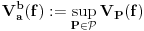 gde je 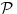 skup svih podela intervala skup svih podela intervala 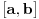 . .U opštem slučaju je 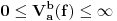 . .Ako je 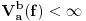 kaže se da je kaže se da je  f-ja ograničene varijacije. f-ja ograničene varijacije.Postoji masa zanimljivih stvari u vezi sa pojmom (ograničene) varijacije pa je zato najbolje da pogledaš odgovarajuću literaturu, a ja ću navesti formulacije dva tvrđenja za koje mislim da imaju veze sa tvojim pitanjem: T1. Neka je 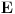 normiran vektorski prostor i normiran vektorski prostor i 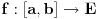 diferencijabilna a diferencijabilna a 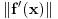 integrabilna f-ja. Tada je integrabilna f-ja. Tada je 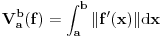 T2. Ako je 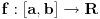 f-ja ograničene varijacije na f-ja ograničene varijacije na 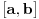 , tada je , tada je 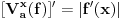 za skoro svako za skoro svako 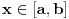 . .[ Djomloun @ 22.07.2006. 12:42 ] @
Da odgovorim sam sebi, kod integrala varijacije bitna je putanja po
kojoj vrsimo integraciju od 1 -> 2 dok kod integrala diferencijala je bitna samo pocetna i krajnja tacka. To ima za posledicu da ako je pocetna i krajnja tacka ista, int. varijacije moze ali ne mora biti nula, dok je int. diferencijala nula! Izvor wikipedia, lnk http://en.wikipedia.org/wiki/First_Law_of_Thermodynamics Citat: The integral of an inexact differential depends upon the particular "path" taken through the space of thermodynamic parameters while the integral of an exact differential depends only upon the initial and final states. If the initial and final states are the same, then the integral of an inexact differential may or may not be zero, but the integral of an exact differential will always be zero. //EDIT: Poslao sam odgovor mailom, pa nisam video da je uranium vec odgovorio. [ Djomloun @ 22.07.2006. 12:47 ] @
Ja nisam basx bio precizan sa pitanjem, mene je u stvari interesovala integracija varijacije i intgracija diferencijala od 1 do 2, hvala na odgovoru u svakom slucaju.
Pozdrav. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|