Potrebna nam je i pretpostavka da je tačka nagomilavanja skupa . Prevedimo date relacije na jezik:





Želimo da pokažemo da važi:

tj.

Neka je proizvoljno i unapred dato.
Uzmimo za trenutak da je i na osnovu nađimo neko takvo da vratimo sada umesto :




Iz uslova sledi da postoji neko tako da .

Time je upravo pokazano da važi .

Mogli smo polazne relacije da prevedemo i na jezik okolina:

Ako je okolina tačke obeležena sa , onda uzimamo da je pa su odgovarajući prevodi:







Dokažimo još jednom da je .

Neka je data proizvoljna okolina , onda postoji neka okolina tako da važi a za okolinu možemo pronaći neku okolinu tako da važi - pa dobijamo da važi a to je i trebalo dokazati.


_{Ovaj drugi dokaz možeš pronaći npr. u knjizi Matematička analiza 1, D. Adnađević, Z. Kadelburg}

Hvala!!!

I jos ako moze dokaz sledeceg tvrdjenja(ako je uopste tacno u svakom slucaju), jer vidim da se to samo podrazumeva, a cesto se koristi.

Naime treba da dokazemo da vazi tvrdjenje T(m) za neki realan broj m, iz uslova da tvrdjenje T vazi za neki skup brojeva koji konvergira u m.




_{[Ovu poruku je menjao qzqzqz dana 30.07.2006. u 17:11 GMT+1]}

Svakako ne važi u opštem slučaju. Neka tvrđenje glasi da je neki broj racionalan, i uzmi gomilu racionalnih brojeva koja konvergira ka .

Može li primer?

Mislio sam na ono kad se kaze "predjimo na limes". Na primer kad se dokazuje Jensen konveksnost+neprekidnost=konveksnost, pa se uoci niz koji tezi itd... Zasto je to korektno?

_{[Ovu poruku je menjao qzqzqz dana 30.07.2006. u 09:28 GMT+1]}

Jel' bi mogao neko da odgovori, posto sutra putujem i necu biti u mogucnosti da dodjem na net, a bas me zanima?

Hajde da vidimo taj tvoj primer:

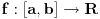
Ako je J-konveksna i neprekidna, onda je i konveksna.

Dokaz.

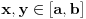
Budući da je J-konveksna imamo da za svako važi .

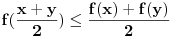
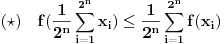
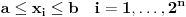
Otuda indukcijom sledi da za jer



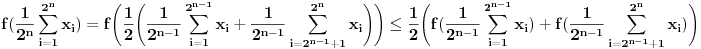
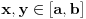
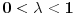
Želimo da pokažemo da za svako i svako važi:

.


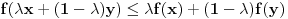
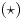
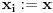
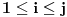
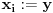
Stavimo zato u nejednakosti da je za svako a da je za svako .
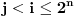
Dobijamo:



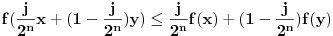
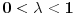
Neka je sada proizvoljno.
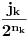
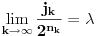
Uvek možemo napraviti niz takav da (npr. koristeći binarnu reprezentaciju broja ).

Zato posmatramo niz nejednakosti:



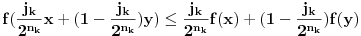
za dovoljno veliko .

Prelaskom na limes i koristeći neprekidnost f-je dobijamo:

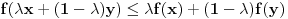
što je i trebalo pokazati.


Ovde su upotrebljena dva stava (koji se lako dokazuju):

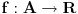
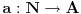
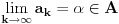
1. Ako je neprekidna i ako je i , onda je .

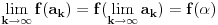
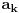
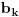
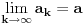
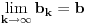
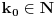
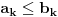
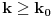
2. Neka su i realni nizovi i neka je i . Ako postoji neko tako da za svako onda je i .


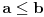
Naravno, postoji još mnogo (u praksi konačno mnogo ) načina da se iskoristi "prelazak na limes", tako da bi (barem meni) bilo teško staviti ih sve u isti "koš". Ako imaš još koji primer - napiši pa ćemo i njega proanalizirati.

_{[Ovu poruku je menjao uranium dana 31.07.2006. u 22:43 GMT+1]}

Jos jednom hvala!!!