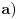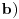[ qzqzqz @ 11.08.2006. 14:12 ] @
|
| Imamo sledeci zadatak:
Dat je jednakostranicni petougao. Da li se sa njim moze poplocati ravan?
Sada posto sam se raspravljao sa nekim profesorima zanima me sta u stvari treba da se uradi:
a) Naci primer nekog petougla za koji je poplocavanje moguce, i time dati potvrdan odgovor na zadatak;
b) Naci skup svih jednak. petouglova za koje je poplocavanje moguce i skup jednak. petouglove za koje nije moguce i videti da li dati petougao pripada prvom ili drugom skupu. |
[ mLAN @ 11.08.2006. 14:52 ] @
Photoshop kaže da ne može


U matematičko dokazivanje ne ulazim...

[ qzqzqz @ 11.08.2006. 17:41 ] @
Ok je da ne moze da se poploca sa pravilnim petouglom, ali mene zapravo vise zanima
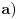
ili
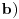
.
[ kime1 @ 11.08.2006. 22:26 ] @
meni liči na a), a pošto je a) lakše, da ne kažem podskup od b), prvo uradi to, a posle ćeš lako :)
[ qzqzqz @ 12.08.2006. 08:05 ] @
Moze na sledeci nacin da se poploca i time bi odgovor na pitanje zadatka bilo
moze (ako je odgovor pod a) tacan).
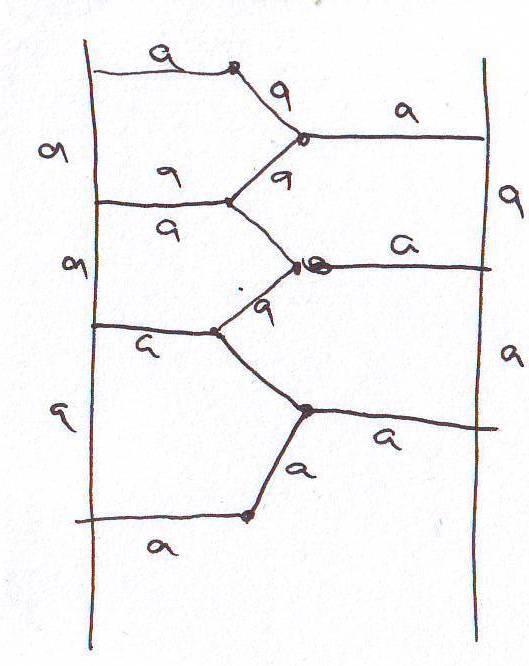
Glavno pitanje je jel' tacno a) ili b), po meni je to b).
[ kime1 @ 12.08.2006. 10:56 ] @
onda bi se zadatak sveo na nalaženje svih mogućih rešenja, jer takvih petouglova ima beskonačno mnogo, osim ako se neka klasa ne podrazumeva kao jedno...
[ Bojan Basic @ 12.08.2006. 12:25 ] @
Postoji 14 do sada poznatih tipova konveksih petouglova koji mogu da popločaju ravan (ne zna se da li su to i jedini). Konveksni petouglovi su, inače, jedini konveksni poligoni za koje nije poznato sve u vezi s popločavanjem ravni — svaki trougao ili četvorougao mogu je popločati, ne postoji mnogougao sa 7 ili više stranica koji je može popločati, a u slučaju šestouglova tačno se znaju klase koje mogu popločati ravan i koje ne.
Što se tiče zadatka, mislim da je nesporno da nije dovoljno precizno postavljen. Ipak, ja bih ga tumačio na treći način: da li se datim jednakostraničnim petouglom uvek može popločati ravan?, i odgovorio bih negativno, navodeći pravilan petougao kao primer. Ni tvoje b) tumačenje nije nelogično, ali mislim da je a) totalno pogrešno. Ako se u zadatku kaže da je dat jednakostranični petougao, onda svakako ne možeš ti da odabereš neki svoj i kažeš „eto, s ovim može“.
I za kraj, da vidimo koji to jednakostranični petouglovi (konveksni) do sada poznati mogu popločati ravan. Velika slova označavaju uglove, u svakoj tački biće naveden jedan od dovoljnih uslova da petougao poploča ravan:
• A+B=180°;
• A+C=180°;
• A≈89° 16', B≈144° 32' 30'', C≈70° 55', D≈135° 22', E≈99° 54' 30''.
[ qzqzqz @ 12.08.2006. 15:41 ] @
Dobro je da ima neko ko se slaze samnom.

Ja sam to citav sat pokusavao da objasnim dvojici profesora i na kraju sam odustao.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.