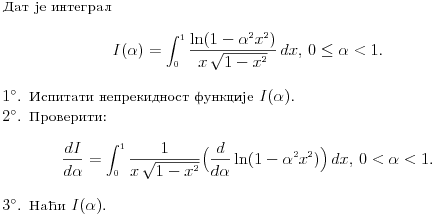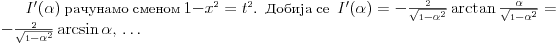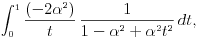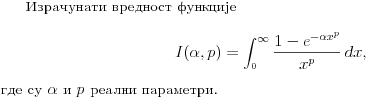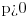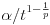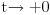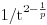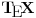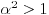[ Cabo @ 20.08.2006. 18:07 ] @
|
[ Cabo @ 22.08.2006. 14:29 ] @
Svi junaci nikom ponikoše...
[ uranium @ 23.08.2006. 10:33 ] @
Nikako ne uspevam da nateram
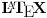 da mi prikaže \rightrightarrows - tako da (privremeno) odustajem da mi prikaže \rightrightarrows - tako da (privremeno) odustajem I) Pošto zadatak ne bi imao smisla ukoliko dati integral ne konvergira - pozabavimo se prvo time. Neka je 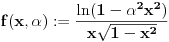 , , 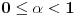 . .Vidimo da je: 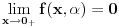 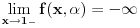 pa je singularitet samo u tački  . Takođe, smatraćemo da je . Takođe, smatraćemo da je 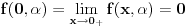 . .Neka je zato  i neka je i neka je 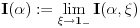 . . Pokazaćemo da je ovaj limes uvek konačan. Dakle, dokažimo da 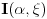 ravnomerno konvergira po ravnomerno konvergira po 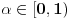 kad kad 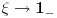 tj. da tj. da 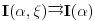 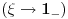 . .Upotrebićemo Vajerštrasov kriterijum i pri tom, budući da na konvergenciju utiče samo ponašanje podintegralne f-je u nekoj okolini singulariteta - posmatraćemo f-ju na intervalu 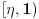 za neko fiksirano za neko fiksirano  . .Za svako 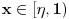 i svako i svako 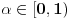 važi: važi: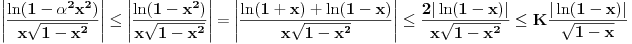 za neko za neko 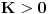 . .To je posledica neprekidnosti (pa samim tim i ograničenosti) f-je 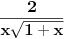 na kompaktnom skupu na kompaktnom skupu  (pa time i na (pa time i na 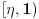 ) a upotrebljeno je i ) a upotrebljeno je i  što je posledica važenja relacije što je posledica važenja relacije 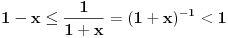 na na 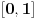 . .Parcijalnom integracijom dobijamo 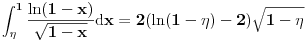 čime je dokazano čime je dokazano 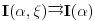 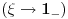 . .U narednim tačkama koristiću neke osnovne teoreme - da ih ne bi prekucavao, pozivaću se na njihovu numereciju u drugom izdanju knjige Matematička analiza 2, D. Adnađević, Z. Kadelburg. 1. Treba ispitati neprekidnost f-je 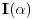 . Možemo da upotrebimo neprekidnost f-je . Možemo da upotrebimo neprekidnost f-je  na na 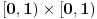 pa rezultat direktno sledi na osnovu teoreme 7.3.2. pa rezultat direktno sledi na osnovu teoreme 7.3.2.A možemo i da se malo pomučimo (ipak je to zadatak sa ispita 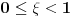  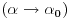 na na 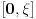 za svako za svako 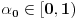 . Evo odakle to sledi: . Evo odakle to sledi:Neka je  dato. dato.F-ja 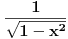 je neprekidna (pa i ograničena nekim je neprekidna (pa i ograničena nekim 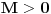 ) na ) na 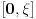 . .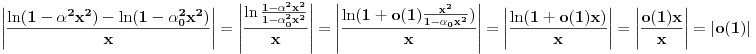 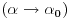 - ovo poslednje sledi iz ograničenosti neprekidne f-je - ovo poslednje sledi iz ograničenosti neprekidne f-je 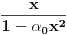 na na 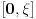 . .Sada je jasno da postoji 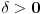 tako da iz tako da iz 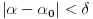 sledi sledi 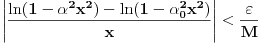 , pa najzad imamo , pa najzad imamo  za svako za svako 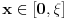 što tačno znači da što tačno znači da  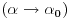 pa iz teoreme 7.3.1 sledi pa iz teoreme 7.3.1 sledi 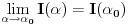 . .2. Ovde bi mogli da upotrebimo teoremu 7.3.3 (dovoljni uslovi za upotrebu Lajbnicovog pravila na nesvojstvene parametarske integrale), ako pokažemo da važe svi potrebni uslovi. i) f-ja 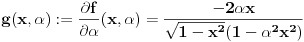 je neprekidna na je neprekidna na 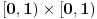 . .ii) Za svako 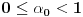 integral integral 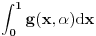 ravnomerno konvergira na ravnomerno konvergira na 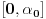 . To sledi na osnovu Vajerštrasovog kriterijuma: . To sledi na osnovu Vajerštrasovog kriterijuma:za svako 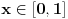 i svako i svako 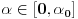 važi važi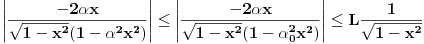 za neko za neko 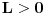 - to sledi iz ograničenosti f-je - to sledi iz ograničenosti f-je 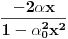 na na 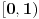 (gledano kao f-ja po (gledano kao f-ja po  ). Ravnomerna konv. sledi zbog konvergencije integrala ). Ravnomerna konv. sledi zbog konvergencije integrala  . .iii) 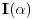 (ravnomerno) konvergira na (ravnomerno) konvergira na 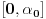 time su provereni svi uslovi pa na osnovu teoreme 7.3.3 sledi tvrđenje pod 2. 3. Sada moramo da izračunamo 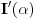 - jer bi nam to moglo pomoći u pronalaženju - jer bi nam to moglo pomoći u pronalaženju 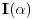 . .U integralu 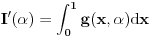 uvodimo smenu uvodimo smenu 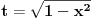 . .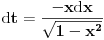 integral postaje  Dakle, imamo da je 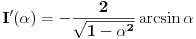 a odatle odmah dobijamo a odatle odmah dobijamo 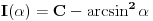 . .Na osnovu definicije f-je 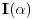 vidimo da je vidimo da je  . .Budući da sam ovo ukucavao/proveravao direktno u polju za upis odgovora - valjda ne moram da objašnjavam koliko sam se napatio [Ovu poruku je menjao uranium dana 24.08.2006. u 02:17 GMT+1] [ Cabo @ 24.08.2006. 10:23 ] @
[ Cabo @ 24.08.2006. 12:08 ] @
Šta mi nije jasno:
1) Zašto je 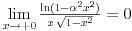 ? Primenom Lopitalovog pravila, ja dobijam: ? Primenom Lopitalovog pravila, ja dobijam: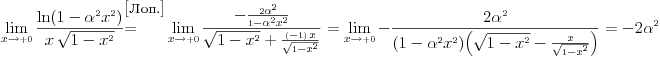 Što je za fiksirano 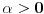 konačan broj manji od nule. konačan broj manji od nule.Još nešto: koliko sam ja shvatio, mi definišemo novu funkciju 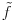 koja je neprekidna, a ne posmatramo više koja je neprekidna, a ne posmatramo višestaru funkciju 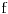 ? Onda je u redu ako napišem ? Onda je u redu ako napišem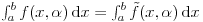 ? ?2) Što se tiče parcijalnog izvoda funkcije 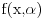 po po  , izgleda da sam pogrešio u računu, jer sam dobio , izgleda da sam pogrešio u računu, jer sam dobio 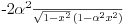 umesto ispravnog umesto ispravnog 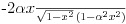 . Integral od onog pogrešnog izvoda, naravno, divergira, a za ovaj tačni izvod Matematika daje: . Integral od onog pogrešnog izvoda, naravno, divergira, a za ovaj tačni izvod Matematika daje:Code: \!\(If[\(\[ InvisibleSpace ]! \((Im[1\/\[ Alpha ]\^2] == 0 && \[ Alpha ]\^2 > 0 && 1\/\[ Alpha ]\^2 < 1) \)\) && Arg[\[ Alpha ]\^2] \[ NotEqual ] 0, \(-\(\(2\ \[ Alpha ]\ ArcSin[\@\[ Alpha ]\^2]\)\/\@\(\[ Alpha ]\^2 - \[ Alpha ]\^4\)\)\), \[ Integral ]\_0\%1 \(-\(\(2\ x\ \[ Alpha ]\)\/\(\@\(1 - x\^2\)\ \((1 - x\^2\ \[ Alpha ]\^2)\)\)\)\) \[ DifferentialD ]x]\) što u prevodu na matematički jezik, i sa izvesnim skraćenjima, znači: 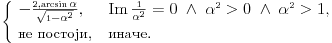 3) I, naravno, ostaje drugi zadatak, za koji u rešenju iz Rokova piše da integral ravnomerno konvergira za 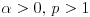 , a ja dobijam za , a ja dobijam za 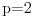 da je da je 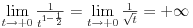 . Pretpostavljam da je potrebno primeniti sličan postupak kao u prvom zadatku, tj. da treba posmatrati parametarski integral na nekom intervalu . Pretpostavljam da je potrebno primeniti sličan postupak kao u prvom zadatku, tj. da treba posmatrati parametarski integral na nekom intervalu 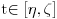 , gde je , gde je 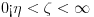 ? Ili ? Ili 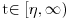 ? ?Inače, ako nekoga interesuje što se uopšte bakćem sa parametarskim integralima, odgovor je da poena nikada nije previše — naročito ako se uzme u obzir zakidanje na sitnicama i usmeni. [Ovu poruku je menjao Cabo dana 24.08.2006. u 13:54 GMT+1] [Ovu poruku je menjao Cabo dana 24.08.2006. u 14:00 GMT+1] [ uranium @ 24.08.2006. 15:38 ] @
Budući da
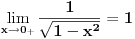 dovoljno je da pronađemo dovoljno je da pronađemo 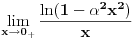 - a primenom Lopitalovog (istoričari kažu u stvari Bernulijevog - a primenom Lopitalovog (istoričari kažu u stvari Bernulijevog 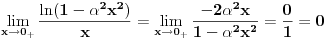 Naravno, mogli smo da primenimo isto pravilo i na celu f-ju  onda bismo dobili: onda bismo dobili: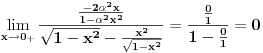 Pošto f-ja  nije ni bila definisana u tačkama nije ni bila definisana u tačkama 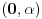 imam pravo da je definišem u njima kako god poželim, pa u konkretnom slučaju mogu baš i tako da postane neprekidna na imam pravo da je definišem u njima kako god poželim, pa u konkretnom slučaju mogu baš i tako da postane neprekidna na 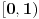 (gledano kao f-ja po (gledano kao f-ja po  ). Dakle, čak i formalno nisam u obavezi da uvodim novu oznaku za f-ju. ). Dakle, čak i formalno nisam u obavezi da uvodim novu oznaku za f-ju. Ako su singulariteti i u  i u i u  podrazumeva se da je po definiciji podrazumeva se da je po definiciji 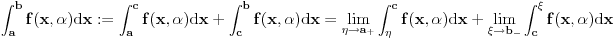 pri čemu je pretpostavljena integrabilnost na svakom pri čemu je pretpostavljena integrabilnost na svakom 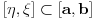 , ,  . S tim u vezi, jasno je da je eventualna definisanost podintegralne f-je u tačkama . S tim u vezi, jasno je da je eventualna definisanost podintegralne f-je u tačkama  i i  potpuno irelevantna (bitno je samo njeno ponašanje u nekim okolinama tih tačaka). potpuno irelevantna (bitno je samo njeno ponašanje u nekim okolinama tih tačaka).Pretpostavljam da si hteo da napišeš (barem Mathematica jeste 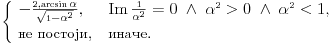 što bi bilo u skladu sa uslovima iz druge tačke tj. 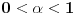 . .Što se tiče poslednjeg pitanja - integral bi se posmatrao kao zbir graničnih vrednosti dva integrala sa konačnim (ne-nula) granicama a primitivna f-ja bi bila asimptotski ekviv. sa 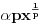 - tako da je sve u redu - tako da je sve u redu [ petarm @ 24.08.2006. 16:34 ] @
Bernulijevog pravila? Gde mogu naci nesto vise o tome?
[ uranium @ 24.08.2006. 16:47 ] @
Citat: Biography of Johann Bernoulli: The well known de l'Hôpital's rule is contained in this calculus book and it is therefore a result of Johann Bernoulli. In fact proof that the work was due to Bernoulli was not obtained until 1922 when a copy of Johann Bernoulli's course made by his nephew Nicolaus(I) Bernoulli was found in Basel. Bernoulli's course is virtually identical with de l'Hôpital's book but it is worth pointing out that de l'Hôpital had corrected a number of errors such as Bernoulli's mistaken belief that the integral of 1/x is finite. After de l'Hôpital's death in 1704 Bernoulli protested strongly that he was the author of de l'Hôpital's calculus book. It appears that the handsome payment de l'Hôpital made to Bernoulli carried with it conditions which prevented him speaking out earlier. However, few believed Johann Bernoulli until the proofs discovered in 1922. [ Cabo @ 24.08.2006. 17:04 ] @
[ uranium @ 24.08.2006. 17:11 ] @
U pravu si - Mathematica je izbacila upravo ono što si ti napisao (izvinjavam se
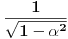 mora biti mora biti 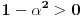 tj. tj. 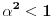 . Mada, ako pratimo sve korake do sad - mi smo oduvek znali da je . Mada, ako pratimo sve korake do sad - mi smo oduvek znali da je 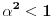 - a to smo i iskoristili prilikom računanja - a to smo i iskoristili prilikom računanja 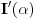 ... ...[Ovu poruku je menjao uranium dana 24.08.2006. u 18:47 GMT+1] Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|