Farenhajte, ovaj tvoj zadatak traži malo fizikalisanja ali u njemu nema ničeg (strašn0) nepoznatog. Nisam baš sve stavio na papir, da nije možda štos u tome da se dobije neka jednačina koja se ne može analitički rešiti po traženom uglu?

Ne, dobija se eksplicitan izraz tipa , a što se fizikalisanja tiče, i ono je zapravo minimalno ako se dosetiš najefikasnijeg pristupa.

Nekako imam utisak da je ovo ipak zadatak iz fizike...

Dakle, ako je verovati fizičarima, vertikala mora proći kroz centar mase.
Radi jednostavnosti posmatraćemo isečak jediničnog kruga.
Postavimo pravougli koordinatni sistem tako da važi:





gde je , .

Pronađimo koordinate centra mase:



slično dobijamo i



imamo i da je površina isečka pa su kordinate centra mase date sa:



Dakle, dovoljno je da pronađemo tup ugao koji prava zaklapa sa pozitivnim delom -ose.



pa kako je imamo da je


@Farenhajt:

Na osnovu tvoje prethodne poruke može se zaključiti da veruješ da imaš i neko lepo elementarno rešenje - pa bih zaista voleo da ga vidim - tim pre što sam jedno vreme mislio da imam nešto u tom smislu (a onda sam se razočarao videvši da dotična vertikala u opštem slučaju ne deli figuru na dva dela jednakih površina... )


_{[Ovu poruku je menjao uranium dana 29.08.2006. u 09:05 GMT+1]}

Pa, da je sasvim elementarno, i nije, ali se može smatrati da je na nivou ozbiljnije potkovanog srednjoškolca-takmičara

Da bismo našli centar mase, najprostije je iskoristiti Papusovu teoremu (čiji se dokaz, naravno, ne može izvesti bez analize, ali s druge strane, ni dokaz formule za zapreminu lopte ne može se striktno izvesti bez analize, pa nas to ne sprečava da je naučimo već u VII razredu i slobodno koristimo).

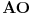
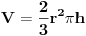
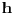
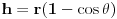
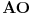
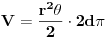
Dakle, ako kružni isečak rotira oko poluprečnika , dobija se sferni isečak čija je zapremina data sa , pri čemu je poluprečnik sfere, a visina odgovarajuće kalote, koja u ovom slučaju iznosi . S druge strane, ako je odstojanje centra mase od prave , imamo da je . Kad izjednačimo dva izraza, dobijamo .

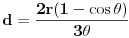
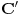
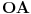
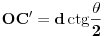
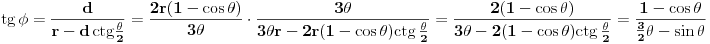
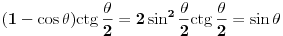
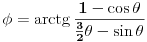
Neka je podnožje normale iz na . Tada je , pa je , pošto je . Dakle, . (Što je, naravno, isto ono do čega je stigao i uranium, samo s drugačijim znacima pod arkustangensom, pošto je on računao tup ugao, a ja oštar.)

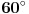
Kuriozitet: Ako je centralni ugao isečka , dobija se, pa recimo "lep" izraz:

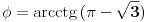_{[Ovu poruku je menjao Farenhajt dana 29.08.2006. u 10:23 GMT+1]}

Svaka čast!
Veliko hvala na lepom zadatku i još lepšem rešenju!

Svaka čast uraniume! Ja sam krenuo da rešavam, ali sam se negde zeznuo u računu, a kada sam na kraju dobio arcctg, pomislio sam da je suviše komplikovano, pa sam odustao. Inače, ti si iskomplikovao stvar jer si računao u pravouglom koordinatnom sistemu. Da si uzeo polarni, težište T bi moralo da bude na simetrali ugla zbog simetričnosti, tako da bi morao da nađeš samo r. Posle toga, dobio bi trougao OAT sa stranicama R, r i uglovima AOT teta pola, TAO pi minus fi, a rešenje se dobija na osnovu toga da su sinusi uglova podeljeni sa dužinom stranice jednaki u oba slučaja...

Edit: sada sam pogledao gde sam pogrešio, zaporavio sam da podelim sa R teta kada sam tražio težište



_{[Ovu poruku je menjao djoka_l dana 29.08.2006. u 19:27 GMT+1]}

U pravu si, pogotovu ako imamo u vidu i sjajno Farenhajtovo rešenje
Kad sam video da zadatak ne pruža otpor - nisam ni razmišljao dalje... a simetričnost sam upotrebio da ("na kvarno" ) izračunam
_{naravno, pre postovanja sam "ispešačio" i regularnu formulu}

Još jedan kuriozitet: Zapravo postoji isečak za koji je (oštar) ugao otklona najveći mogući (tj. funkcija ima lokalni maksimum na ), a njegov centralni ugao rešenje je transcendentne jednačine , koje približno iznosi