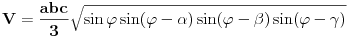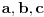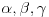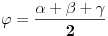[ Farenhajt @ 29.08.2006. 20:07 ] @
|
[ uranium @ 30.08.2006. 05:12 ] @
Neka je
 vrh piramide i neka je: vrh piramide i neka je: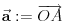 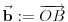 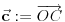 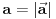 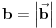 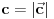 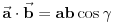 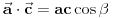 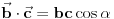 Ako je  podnožje visine piramide iz temena podnožje visine piramide iz temena  , onda definišemo , onda definišemo 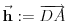 . Označimo i . Označimo i 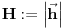 Jasno je da postoje jedinstveni 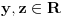 za koje važi za koje važi 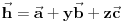 . Nakon skalarnog množenja poslednje jednakosti sa . Nakon skalarnog množenja poslednje jednakosti sa 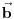 , odnosno sa , odnosno sa 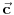 dobijamo sistem: dobijamo sistem: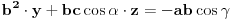 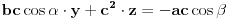 pa zatim i rešenje: 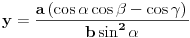 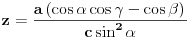 Nakon (ne baš kratkog) računa dobijamo: 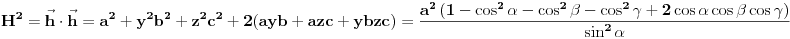 Ako je 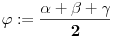 , onda, koristeći adicione formule (u širem smislu , onda, koristeći adicione formule (u širem smislu 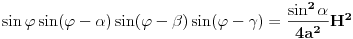 Kako je 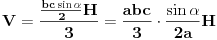 jasno je da formula iz postavke zadatka zaista važi. jasno je da formula iz postavke zadatka zaista važi.@Farenhajt: Nadam se da imaš neko humanije rešenje [Ovu poruku je menjao uranium dana 30.08.2006. u 07:21 GMT+1] [ Farenhajt @ 30.08.2006. 14:23 ] @
Pa, imam samo malčice humanije rešenje. Pre svega, i dalje ostaje da se "peške" dokaže da je
 . Međutim, ostala računica može se donekle uprostiti ako se uzme u obzir sledeće: Ukoliko se jedna bočna ivica neke trostrane piramide produži . Međutim, ostala računica može se donekle uprostiti ako se uzme u obzir sledeće: Ukoliko se jedna bočna ivica neke trostrane piramide produži  puta, a druge dve ostanu nepromenjene, zapremina će se povećati puta, a druge dve ostanu nepromenjene, zapremina će se povećati  puta - što je očigledno ako se za bazu uzme trougao određen dvema nepromenjenim bočnim ivicama. Dakle, dokaže li se stav za puta - što je očigledno ako se za bazu uzme trougao određen dvema nepromenjenim bočnim ivicama. Dakle, dokaže li se stav za 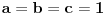 , dokazan je uopšte. Stoga analitički pristup postaje malo lakši: Uzmimo tačke , dokazan je uopšte. Stoga analitički pristup postaje malo lakši: Uzmimo tačke 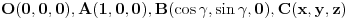 i postavimo uslove preko intenziteta i skalarnih proizvoda: i postavimo uslove preko intenziteta i skalarnih proizvoda: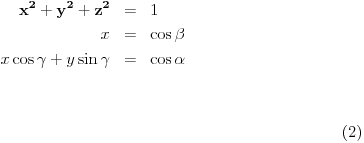 i čini mi se da se računica donekle pojednostavljuje jer se onda visina direktno dobija kao  , a površina baze je, jasno, , a površina baze je, jasno, 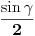 . .Dodatak: Ni ona trigonometrijska formula nije odveć komplikovana za dokaz - dovoljno je dvaput transformisati proizvod u zbir, i posle toga se uglavnom sve lepo sredi. [Ovu poruku je menjao Farenhajt dana 30.08.2006. u 17:18 GMT+1] [ uranium @ 30.08.2006. 20:44 ] @
Vrlo lepo
Redukcija 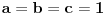 i posmatranje koordinata zaista značajno skraćuju račun! i posmatranje koordinata zaista značajno skraćuju račun!Citat: Farenhajt: Dodatak: Ni ona trigonometrijska formula nije odveć komplikovana za dokaz - dovoljno je dvaput transformisati proizvod u zbir, i posle toga se uglavnom sve lepo sredi. Ah...vidim da je i tebe ona moja prvobitna šala ostavila u nedoumici : Citat: nakon što mi je skrenuta pažnja da nije baš jasno da se radi o šali (pa čak ni u čemu je Da ne zaboravim još nešto: formula je baš lepa pa me zanima ima li neko ime? Zna li se njen autor? [ Farenhajt @ 31.08.2006. 09:06 ] @
Nisam ni video tu prvobitnu šalu, koja se meni lično više dopada i sasvim mi je razumljiva
U vezi s nazivom formule i autorom nemam podatak, pokušaću da ga pronađem, mada je po formi vrlo "heronoidno-bramaguptična", so to speak [ djoka_l @ 31.08.2006. 11:02 ] @
Pokušao sam da nađem tu formulu na netu, ali se pominje samo verzija sa cos, dok ove sinusne nema. Baš šteta, jer se mnogo lakše pamti, a ne može joj se poreći ni estetika. Stvarno deluje čudesno kao veza između površine trougla i zapremine piramide.
[ Farenhajt @ 31.08.2006. 16:13 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|