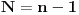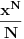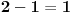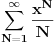[ glock @ 31.08.2006. 17:15 ] @
| Molim za razumevanje jer je pitanje za matematicare sigurno levatsko. :) Kako da transformisem sledecu sumu : S za n=1 do n=beskonacno {(x na n-1) / (n-1) } u sumu oblika S za n=1 do n=beskonacno {(x na n)/(n)} +/- valjda neki ostatak {} zagrade sam koristio za oznacim izraz koji mi se nalazi u sumi; () zagrade imaju standardno znacenje Jos ako neko moze da mi objasni/linkuje objasnjenje za slicne transformacije, hvala mnogo. |