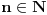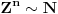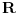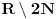[ petarm @ 04.09.2006. 12:37 ] @
| Na ovom forumu vec su dati neki dokazi da skup R nije ekvipotentan sa skupom N. Mene zanima da li bi neko mogao da dokaze sledece: Teorema. Transcedentnih iracionalnih brojeva ima koliko i svih realnih brojeva. Prikacio sam dokaz da iracionalnih brojeva ima kolko i realnih. |