Preciznije, to su posledica simetrija prostora i vremena u nerelativističkoj, tj. simetrija prostor-vremena u relativističkoj mehanici. Konkretno radi se o homogenosti prostora i vremena (prostor-vremena u relaivističkom slučaju) i o izotropnosti prostora. Homogenost prostora znači da izolovani fizički sistem možemo slobodno translirati po prostoru ali da to neće menjati zakone kretanja sistema (tj. ne postoje tačke u prostoru koje bi neki fizički eksperiment mogao da izdvoji na neki način). Homogenost vremena znači da kako god izabrali početni trenutak (ovo bi u stvari bile vremenske translacije) kretanja izolovanog sistema, zakoni kretanja tog sistema će biti isti (tj. ne postoje trenutci koji bi se eksperimentom izdvojili). U relativističkoj mehanici prostor i vreme su objedinjeni u prostor-vremenu tako da se prostorne i vremenske translacije ujedinjuju u prostor-vremenske translacije (tj. translacije u 4D prostoru). Izotropnost prostora znači da fizički sistem možemo slobodno rotirati i da to neće uticati na zakone kretanja sistema (tj. eksperimentom ne možemo izdvojiti neki pravac u prostoru). Na primer, zamisli jedan izolovani linearni harmonijski oscilator. Homogenost prostora znači da možemo slobodno da stavimo LHO bilo gde u prostoru, ali njegova amplituda i frekvencija oscilovanja će uvek biti iste. Homogenost vremena će značiti da LHO možemo da pustimo da osciluje u bilo kom trenutku ali da to takođe neće promeniti njegovu amplitudu i frekvenciju. Analogno je sa postavljanjem LHOa u proizvoljni pravac i izotropijom prostora.
Homogenost prostora za posledicu ima zakon odžanja impulsa, homogenost vremena zakon održanja energije (ovo je u relativističkoj mehanici objedinjeno u zakon održanja energije-impulsa), a izotropnost prostora zakon održanja momenta impulsa.
Ako želiš napisaću dokaz.

Sto da ne!

Uf, ne mogu da verujem da sam ovoliko pozaboravljao teorijsku mehaniku. Jedva sam se setio dokaza. Elem,

I. Pošto ne znam da li studiraš fiziku (ili eventualno građevinu) prvo ide jedan crash-course iz analitičkog formalizma u klasičnoj mehanici (ako ti je poznato, preskoči).

Osnova svega je funkcija pod imenom lagranžijan i ona se definiše kao L=T-U, gde je T kinetička energija sistema, a U potencijalna energija sistema. Pri tome se uzima da su nezavisne promenljve koordinate sistema, brzine sistema i vreme (to mogu biti proizvoljne koordinate, ali ja ću ovde uzeti dekartove koordinate), tj. gde i=1...n, gde je n broj čestica u sistemu. Iz ove funkcije se dobijaju jednačine kretanja izolovanog sistema pomoću lagranževe jednačine



Na, primer uzmimo jednodimenzionalni LHO. Neka osciluje duž x-ose oko tačke x=0. Tada je njegova kinetička energija , a potencijalna što rezultuje lagranžijanom . Tada je , i , što daje jednačine kretanja

,

što je nadam se znaš jednačina kretanja 1D LHOa. Dakle, formalizam radi. Kako je lagranžijan osnova svega, veličine poput impulsa, momenta impulsa i energije se dobijaju iz njega na sledeći način. Impuls i-te čestice sistema se definiše kao



pri čemu oznaka označava gradijent po promenljivima, tj. . Proverimo ovo za LHO. što je naravno impuls LHO kakav znamo da izračunamo na klasičan način. Pošto znamo da formula za izračunavanje impulsa radi, nije problem da izračunamo i moment impulsa , što s obzirom na prethodno daje moment impulsa i-te čestice



Energija i-te čestice se definiše kao



što kada primenimo na LHO daje što posle izračunavanja daje , što se naravno poklapa sa energijom LHOa koju umemo da računamo na klasičan način.

II. Sada da pređemo na stvar

1. Translatorna simetrija i zakon održanja impulsa.

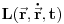
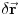
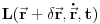
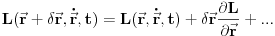
Neka imamo sistem sastavljen od jedne čestice (jednostavnosti radi) i neka je njegov lagranžijan . Neka smo sistem translirali za neko malo , tako da je sada lagranžijan . Razvijmo lagranžijan oko počenih koordinata: . Zahtev za translacionom simetrijom nalaže da ova translacija ne sme promeniti jednačine kretanja, što znači da lagranžijam mora ostati isti, što onda zahteva da svi članovi u razvoju osim prvog moraju biti jednaki nuli. Među njima je i drugi član, što znača da moramo imati . 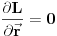Ako se vratimo na lagranževe jednačine, vidimo da je ovo jedan od članova u njoj. Pošto je on nula, tada lagranževa jednačina postaje



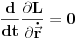
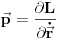
Pošto je impuls sistema definisan sa gornja jednačina postaje



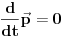
što je zakon održanja impulsa. Dakle, zahtev za translatornim invarijantnošću povlači zakon održanja impulsa.

2. Rotaciona simetrija i zakon održanja momenta impulsa

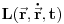
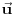
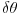
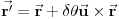
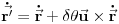
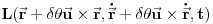
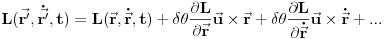
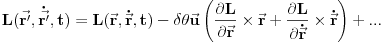
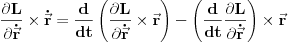
Opet razmatramo sistem sastavljen od jedne čestice sa lagranžijanom . Zarotirajmo sistem oko ose za neki mali ugao . Tada koordinata i brzina trpe sledeće promene i . Lagranžijan sada postaje . Razvijmo lagranžijan oko početnog položaja . Sada ćemo malo reorganizovati izraz koristeći činjenicu da su drugi i treći član mešoviti proizvodi . Pozabavimo se sada drugim članom u zagradi . Korišćenjem ovoga, izraz u zagradi postaje . 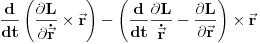Druga zagrada u prethodnom izrazu je u stvari leva strana lagranževe jednačine tako da je to nula što nas na kraju ostavlja sa razvojem . 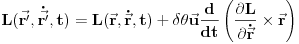Rezonom kao u gornjem slučaju se pokazuje da rotaciona simetrija zahteva da drugi član razvoja bude jednak nuli što da je jednačinu



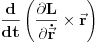
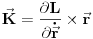
Pošto je moment impulsa definisan sa gornja jednačina postaje zakon održanja impulsa



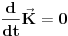
Dakle: Rotaciona simetrija => zakon održanja momenta impulsa.

3. Simetrija u odnosu na vremenske translacije i zakon održanja energije

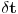
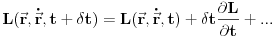
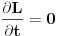
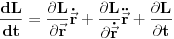
Počinjemo kao u prethodna dva slučaja. Napravimo vremensku translaciju sistema za neko malo i potom razvijemo lagranžijan oko početnog vremena . Rezonom kao u sličajevima 1. i 2. zaključujemo da simetrija u odnosu na vremenske translacije povlači da drugi član u razvoju mora biti jednaku nuli, što znači da je . Sada razmotrimo totalni izvod lagranžijana po vremenu . Videli smo da je treći član na desnoj strani nulti. Transformišimo drugi član . 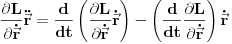Kada ovo vratimo u izraz za totalni izvod lagranžijana po vremenu i malo sredimo, dobijamo . 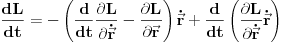Prva zagrada je leva strana lagranževe jednačine, tako da se ona anulira da na desnoj strani izvoda lagranžijana po vremenu ostaje samo poslednji član. Kada se svi članovi prebace na istu stranu dobija se



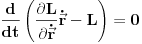
Ako se prisetimo definicije energije



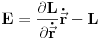
Gornja jednačina postaje



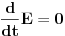
što je zakon održanja energije. Dakle: Simetrija u odnosu na vremenske translacije => zakon održanja energije.

To je do na grešku u kucanju nerelativistički dokaz.

Bravo