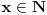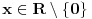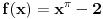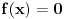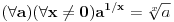[ Farenhajt @ 14.09.2006. 22:15 ] @
|
[ Not now, John! @ 14.09.2006. 22:48 ] @
I mene su učili da je to ekvivalentno.
[ losmipfc @ 14.09.2006. 23:29 ] @
I ja sam ucio da je to jednako, a volio bih kada bi neko pokazao drugacije.
[ chupcko @ 15.09.2006. 11:14 ] @
Uf i ja sam ucio da je nula u skupu prirodnih brojeva, jel to znaci da sam ucio u Bugarskoj ili Rumuniji ?
Donekle je Rumun u pravu, kada su uveli koren to je izgledalo kao 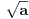 a mislilo se na a mislilo se na 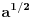 , kasnije su krenuli sa: , kasnije su krenuli sa: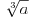 pa i pa i 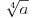 . Ali stvarno nisam nigde video u literaturi recimo . Ali stvarno nisam nigde video u literaturi recimo 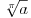 ili ili 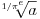 . .Inace mozemo reci da se 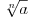 definise kao definise kao 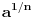 uz odgovarajuce uslove (ne je prirodan broj veci od 1). uz odgovarajuce uslove (ne je prirodan broj veci od 1).Definicija je samo u jednom smeru, nismo rekli da se i 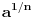 definise sa ... . definise sa ... .[ uranium @ 15.09.2006. 11:26 ] @
Bilo bi dobro ako neko može da se seti gde je video da su ti zapisi ekvivalentni - jer u domaćim knjigama koje sam (za ovu priliku
Meni se ne sviđa što je to tako, ali jasno je da za to postoje očigledni istorijski razlozi. Kažem "uglavnom", jer recimo Dragoljub Aranđelović (čuveni profesor mat. fak. u Beogradu) definiše korene 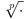 samo za samo za 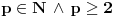 iako način na koji to radi dopušta i slučaj iako način na koji to radi dopušta i slučaj 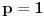 . Šta više, stepene f-je definiše isključivo sa eksponentom iz skupa . Šta više, stepene f-je definiše isključivo sa eksponentom iz skupa 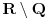 iako način na koji to radi dopušta da eksponent bude iz iako način na koji to radi dopušta da eksponent bude iz 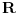 njegovi motivi su jasni, ako imamo u vidu da je čovek nesuđeni logičar njegovi motivi su jasni, ako imamo u vidu da je čovek nesuđeni logičar Da ponovim što reče chupcko: uzrok zabune je verovatno u tome što se svaki izraz oblika 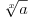 može zapisati kao može zapisati kao 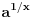 , dok obrnuto ne važi , dok obrnuto ne važi @Farenhajt: Ono što Virgil Nicula nikako nije hteo da prizna je da je sve to samo stvar definicije Što se tiče nule i ja volim kad je i ona u skupu prirodnih, međutim po većini domaćih knjiga to nije tako... Negde sam čuo da Francuzi svrstavaju nulu u prirodne... [ fantomas86 @ 15.09.2006. 14:40 ] @
Oba iskaza su tacna...Samo sto je covek hteo da u drugom slucaju odbaci mogucnost pojavljivanja "neodregjenog"...
Lupitalova pravila(ne omalovazam nikog, samo ne znam koliko ste upuceni) koja definisu slucajeve kao 0*~, ~*~, i tako dalje...ima ih sedam... Po meni...to je morao da definise na dva nacina, jer su u pitanju dve razlicite f-je...(koren i exponencijalna) [ fantomas86 @ 15.09.2006. 14:43 ] @
I da...potpuno vas podrzavam da je 0 u N...hehe
Tako sam i ja ucio... [ Farenhajt @ 15.09.2006. 15:00 ] @
Znači, ono što je nekad bio
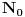 sada je sada je 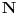 ? Izgleda da je "nova škola" stupila na scenu... Mene (svojevremeno) učili da imamo skup pozitivnih celih (tj. prirodnih) brojeva, pa nulu, pa skup negativnih celih brojeva. Then again, nauka ide napred, verovatno je usled opšte srpske situacije u poslednjih 15 godina prihvaćeno da je prirodno biti nula ? Izgleda da je "nova škola" stupila na scenu... Mene (svojevremeno) učili da imamo skup pozitivnih celih (tj. prirodnih) brojeva, pa nulu, pa skup negativnih celih brojeva. Then again, nauka ide napred, verovatno je usled opšte srpske situacije u poslednjih 15 godina prihvaćeno da je prirodno biti nula [ Bojan Basic @ 16.09.2006. 11:58 ] @
Nisu samu Rumuni i Bugari uključili nulu u prirodne brojeve, sad se više bukvalno ne zna ni ko pije ni ko plaća. Nije čak redak slučaj da dva profesora s istog fakulteta, štaviše s iste katedre, smatraju (i predaju!) različito.
Što se tiče originalnog pitanja (koren), očigledno su i tu posredi različite konvencije (ili definicije, kako vam volja) različitih ljudi. Lično meni je totalno nelogično da te dve stvari znače različito. Koliko puta neko napiše 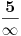 i niko se ne buni, ili napiše i niko se ne buni, ili napiše  ako funkcija nije definisana u ako funkcija nije definisana u  podrazumevajući da je u toj tački vrednost funkcije jednaka limesu? I šta sad, ako ja napišem podrazumevajući da je u toj tački vrednost funkcije jednaka limesu? I šta sad, ako ja napišem 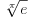 neko će reći da ne zna šta time hoću da kažem? Besmisleno. neko će reći da ne zna šta time hoću da kažem? Besmisleno.[ uranium @ 17.09.2006. 03:17 ] @
@Bojan Basic:
Mislim da se može napraviti sledeća analogija. Neki ljudi ne poštuju pravopis Citat: uranium: Šta više neki poštuju Citat: Bojan Basic: štaviše a neki su ekstremisti [att_img] Te sitnice uglavnom ne utiču na razumljivost napisanog, ali (pored toga što nekima redovno bodu oči Neka je 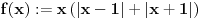 Broj rešenja jednačine 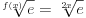 je: je:a)  b)  c)  d)  e) 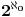 [ Bojan Basic @ 17.09.2006. 12:59 ] @
Potpuno shvatam da je reč o trik-pitanju, ali samo zbog načina na koji si ga postavio; inače ne vidim u čemu je trik.
Moj konačan odgovor je jedno rešenje ( 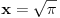 ). Ipak, jako bi mi bilo drago kad bi mi objasnio kako si došao do ostalih odgovora. :) ). Ipak, jako bi mi bilo drago kad bi mi objasnio kako si došao do ostalih odgovora. :)Evo i jednog zadatka za tebe. Pronaći rešenja jednačine 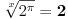 a) u skupu 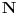 ; ;b) u skupu 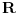 . .Kad ovo rešiš ;), voleo bih da preformulišeš zadatak tako da bude u skladu s drugom varijantom (o kojoj ovde raspravljamo). Poenta: ako koristimo „proširenu“ oznaku nije nikakav problem da ograničimo domen ukoliko nam se ne sviđa sve. Ako pak domen ograničavamo samom oznakom, onda ne postoji način da za širu stvar upotrebimo istu oznaku, u slučaju da nam ona iz nekog razloga zatreba. I kao šlag na tortu, ako u Mathematici ukucamo 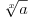 kao rezultat dobićemo kao rezultat dobićemo 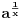 . Naravno, ne pokušavam da kažem da je Mathematica univerzalno rešenje za sve, ali nije loše ni to uzeti u razmatranje. . Naravno, ne pokušavam da kažem da je Mathematica univerzalno rešenje za sve, ali nije loše ni to uzeti u razmatranje.[ uranium @ 17.09.2006. 14:53 ] @
Evo u duhu ove teme - sad sam i ja ostao zbunjen "rešenjem"
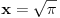 Verujem da je u pitanju lapsus "calami" Pošto još uvek niko nije naveo primer knjige ili članka ili zadatka sa takmičenja ili... gde se pojavljuje izraz 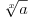 za neko za neko 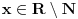 a u isto vreme u svakoj knjizi koju sam pogledao a u kojoj postoji definicija korena, jasno stoji da je indeks prirodan broj. a u isto vreme u svakoj knjizi koju sam pogledao a u kojoj postoji definicija korena, jasno stoji da je indeks prirodan broj.Rešenja koja sam naveo su rezultat poigravanja sa domenom indeksa  : :a) 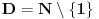 b) 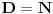 c) 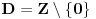 d) 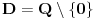 e) 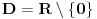 zadatak se svodi na 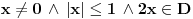 pa otuda i ponuđeni odgovori. pa otuda i ponuđeni odgovori.Dakle, zvanično rešenje je ono pod b) tj. j-na ima rešenja 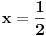 i i  . .Na osnovu većine prethodnih postova na ovoj temi, stiče se utisak da broj rešenja zapravo zavisi od geografskih koordinata... Ako se držimo zvanične definicije korena, tvoj zadatak nema rešenja ni pod a) ni pod b). Ukoliko se odlučimo za proširenu, imamo samo jedno rešenje  . .u delu sa preformulacijom nije mi jasno šta si hteo da kažeš Što se tiče same oznake, koliko mi je poznato, u pitanju je stilizovano slovo r (radix). Jedno pitanje: zbog čega bi se uopšte uvodile stepene f-je ako je koren (kako se ovde tvrdi) definisan za vrednosti indeksa iz celog 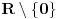 ? ?Ranije sam pominjao nekakve istorijske razloge - tu nisam mislio na puku tradiciju već dug i mučan razvoj teorije iracionalnih brojeva. Da li je potrebno pominjati otpore prema negativnim brojevima? Pa i u samim nazivima se vidi kakav je odnos bio prema kojim brojevima. Što se tiče programa Mathematica voleo bih prvo da mi pokažeš kako se iracionalni brojevi čuvaju u ograničenoj memoriji, ili ako više voliš - kako se uz njihove algoritamske definicije radi sa njima u konačnom vremenu Verujem da su ključne reči odgovora - simbolička manipulacija... ovde bih mogao da napišem neke ružne i jednostrane poglede na simboličku manipulaciju ali me trenutno mrzi Setimo se i toga da je Wolfram fizičar a ne matematičar pa mu nećemo mnogo zameriti što umesto 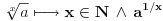 piše samo piše samo  Čisto da pitam (mada pravila dobre advokature nalažu da se postavljaju samo pitanja na koja se zna odgovor 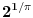 da li ti Mathematica izbaci da li ti Mathematica izbaci 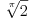 ? ? nadam se da tekst tvog odgovora neće sadržati string "==" [ Bojan Basic @ 17.09.2006. 15:21 ] @
Citat: uranium: Evo u duhu ove teme - sad sam i ja ostao zbunjen "rešenjem" 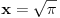 :) :)Verujem da je u pitanju lapsus "calami" :) Možda je krajnje vreme da kupim naočare. :) Na desnoj strani, gde piše 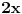 , pročitao sam , pročitao sam  . :) . :)Citat: uranium: u delu sa preformulacijom nije mi jasno šta si hteo da kažeš Pokušao sam da pokažem zašto je „moja“ definicija bolja od „tvoje“ — ako se držimo „moje“ a treba nam „tvoja“ to možemo lako postići: samo dodamo rečenicu koja ograničava domen. Ako se držimo „tvoje“ a treba nam „moja“, ne vidim kako bismo to izveli, osim menjanjem oznake. Citat: uranium: Što se tiče same oznake, koliko mi je poznato, u pitanju je stilizovano slovo r (radix). Jedno pitanje: zbog čega bi se uopšte uvodile stepene f-je ako je koren (kako se ovde tvrdi) definisan za vrednosti indeksa iz celog 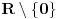 ? ?Zašto neko piše 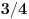 a neko a neko 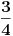 (a neko čak i (a neko čak i 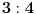 )? To što se isto može reći na drugi način ne znači da ovaj prvi simbolizuje nešto petnaesto. )? To što se isto može reći na drugi način ne znači da ovaj prvi simbolizuje nešto petnaesto.Citat: uranium: Čisto da pitam (mada pravila dobre advokature nalažu da se postavljaju samo pitanja na koja se zna odgovor :)): ako napišeš recimo 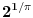 da li ti Mathematica izbaci da li ti Mathematica izbaci 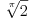 ? :) ? :)Neće, naravno. Mathematica prikazuje izraze na ekranu na uniforman način, a ti možeš da ih unosiš kako hoćeš (ne znam što ti ovo pričam kad verovatno znaš i sam :)). Naravno, ako uneseš 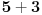 to neće interpretirati kao to neće interpretirati kao 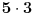 , već pravi „prevod“ samo između ekvivalentnih izraza. Samim tim možemo da zaključimo da smatra da su izrazi o kojima se ovde raspravlja ekvivalentni. Wolfram jeste fizičar, ali čini mi se da je Mathematica jedan od najpopularnijih programa ove namene, i sigurno ne možemo tek tako odbaciti nešto što kaže. , već pravi „prevod“ samo između ekvivalentnih izraza. Samim tim možemo da zaključimo da smatra da su izrazi o kojima se ovde raspravlja ekvivalentni. Wolfram jeste fizičar, ali čini mi se da je Mathematica jedan od najpopularnijih programa ove namene, i sigurno ne možemo tek tako odbaciti nešto što kaže.Evo još jednog mišljenja: http://mathforum.org/library/drmath/view/60847.html [Ovu poruku je menjao Bojan Basic dana 17.09.2006. u 17:33 GMT+1] [ chupcko @ 17.09.2006. 18:22 ] @
Uf, puno zabuna, ajde da pokusam da se prisetim metodike matematike, bilo je davno :))).
Sve zavisi gde i kako uvodimo koren, ali recimo da prvo uvodimo stepenovanje prirodnim brojevima, pa onda sa celim, pa sa racionalnim. Koren se skoro uvek uvodi posle uvodjenja stepenovanja racionalnim brojevima. Naravno posle toga se krece na stepenovanje realnim brojevima, pa se onda definicija korena prosiri i za realne brojeve :). U svakom slucaju cesto se desava da recnik matematike shvatamo previse univerzalnim a on i nije bas toliko. Zato svaki dobrostojeci udzbenik pocinje od pocetka :)). Sto se tice 0 i prirodnih brojeva, pogledajmo original : http://en.wikipedia.org/wiki/Peano_axioms 0 ulazi u prirodne brojeve, a sada sto je nekada neko u cilju lakseg poducavnja 10-togodisnjaka izbacio 0 iz prirodnih brojeva ..., vise na http://en.wikipedia.org/wiki/Natural_number Generalno je dosta tesko nekome mladome objasniti 0 kao pojam, probajte nekom detetu da objasnite da on ima 0 jabuka (hm cak i u jeziku, postoji jednina i mnozina, a ne i nistina). Uostalom svi kada brojim pocinjemo sa 1, 2, 3, ... I ja sam u osnovnoj a moguce i u srednjoj ucio da je skup prirodnih brojeba 1, 2, ... a N0 je ... . Ali na faksu defitnio je uvek 0 ulazila u skup prirodnih brojeva. [ uranium @ 17.09.2006. 21:12 ] @
@Bojan Basic:
Citat: Bojan Basic: Možda je krajnje vreme da kupim naočare. Zaista je nečitko - možda je i to sprečilo uopštavanje definicije korena Koja je definicija bolja - to nije ni bilo sporno. Želeo sam samo da ukažem na zvaničnu definiciju, kao i na to šta se može desiti ako nema standardnog tumačenja. Što se tiče onih primera sa raznim zapisima razlomaka, za razliku od proširene def. korena, lako ćeš pronaći literaturu u kojoj (kad god se radi o strukturama sa komutativnom multiplikativnom operacijom) eksplicitno stoji baš kako si i napisao (dakle, 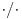 i i 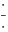 ne znače uvek isto). ne znače uvek isto).Moram da priznam da me iznenađuje tvoj rezon u vezi sa programom Mathematica, ali je besmisleno da se bavimo time kad se već (nadam se) slažemo po osnovnom pitanju ove teme. @chupcko: Citat: chupcko: Koren se skoro uvek uvodi posle uvodjenja stepenovanja racionalnim brojevima. Svestan sam da mnogo tražim, ali evo, navedi mi makar jedan udžbenik gde se korenovanje uvodi posle stepenovanja racionalnim brojevima - zar ti se ne čini da bi u tom slučaju uvođenje korena bilo krajnje nepotrebno? Citat: chupcko: ...a sada sto je nekada neko u cilju lakseg poducavnja 10-togodisnjaka izbacio 0 iz prirodnih brojeva ...kako li su ih onda učili da pišu koliko godina imaju? Citat: chupcko: Uostalom svi kada brojimo pocinjemo sa 1, 2, 3, ... Citat: Math Jokes: The great Polish mathematician Waclaw Sierpinski was coincidentally also absent-minded and coincidentally also had to move house. His wife knew of his fallibility as they stood on the street with all their belongings, said to him, "Now, you stand here and watch our ten cases, while I go and get a taxi." She left him there, eyes glazed and humming absently. Some minutes later she returned, a taxi having been called. Sierpinski challenged her (possibly with a glint in his eye): "I thought you said there were ten cases, but I've only counted to nine." His wife insisted there were ten. "No, count them," replied Sierpinski, "0, 1, 2, ..." [ chupcko @ 17.09.2006. 22:48 ] @
Pa uf, kada bese ono uvedena nula kao broj, zaboravih, davno sam ucio istoriju matematike :).
Sto se tice 0, nemoj da mesas broj 0 sa cifrom 0 :). Uostalom ta dvostruka uloga 0 je i mene kao malog zbunjivala, uvek sam mislio da je 0 nesto veliko cim se 10 koji je veliiiiiiiiki broj pise sa njom. A za udzbenik, ne znam, kada sam bio mali nisam citao te knjige, kada sam na faksu spremao metodiku nisam imao ni jedan, nego sam slusao profesora, a sada nemam vremena :). A iskreno celobrojno stepenovanje se lakse uvodi deci nego koren :). Uvek mozes analogiju izmedju sabiranja i mnozenja, pa onda mnozenja i stepenovanja. Dok za koren moras da uvodis nesto kao : resiti jednacinu x*x = 16. Nego cisto da podsetim, mislim da nema zvanicne definicije korena :). Eto lepog mesta da se u matematiku uvedu standardi :). Ima samo definicija unutar neke knjige, definicija koje koriste pojedini ljudi/skole/nacije/drzave/.../stagod. Inace ja kada sam bio mali hteo sam da uvedem novu operaciju koja resava jednacinu 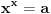 . Ali niko nije smatrao da je to ikome potrebno :). . Ali niko nije smatrao da je to ikome potrebno :).[ Bojan Basic @ 18.09.2006. 01:28 ] @
Citat: uranium: Moram da priznam da me iznenađuje tvoj rezon u vezi sa programom Mathematica, ali je besmisleno da se bavimo time kad se već (nadam se) slažemo po osnovnom pitanju ove teme. I meni se čini da se slažemo po osnovnom pitanju, ali ne znam što ti se toliko ne sviđa rezon s Mathematicom. Ako te ne mrzi voleo bih da i to razrešimo. Citat: Misliš x↑↑2=a? :) [ uranium @ 18.09.2006. 10:16 ] @
@Bojan Basic:
Neke od ranijih verzija Mathematica-e imale su interesantan bug: po njima je bilo 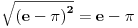 . .Da li iko može da garantuje da više nema takvih bisera? Svi znamo da je dokazivanje korektnosti programa veoma težak a u opštem slučaju zapravo i nerešiv problem. Na kraju, sve definicije su uneli ljudi (nešto ne verujem da u dubini radi neki cellular automata engine i usput otkriva matematičke zakone Takođe, nadam se da ne može da te prevari "efekat kineske sobe". Da stvari nisu bile uvek kao danas (po pitanju indeksa korena) svedoči sledeće: Citat: The radical symbol: By the close of the 17th century the symbolism was, therefore, becoming fairly well standardised, although there still remained some work to be done. The 18th century saw this accomplished, and it also saw the negative and fractional exponent come more generally into use. History of Mathematics volume II, Smith, D.E., Dover Publications 1958 ...naravno, samo pod uslovom da Smith eksponentom zove ono što ja zovem indeksom Pogledao sam malo i Ojlerov Uvod u analizu beskonačno malih iz 1748. - čovek je vrlo dosledno upotrebljavao notaciju sa stepenima kad god bi imao posla sa eskponentima čija recipročna vrednost (ako postoji) pripada skupu  - mislim da je svima poznato koliki je bio uticaj te knjige... - mislim da je svima poznato koliki je bio uticaj te knjige...@chupcko: Citat: chupcko: A iskreno celobrojno stepenovanje se lakse uvodi deci nego koren sa ovim se, naravno, slažem - pa sad imam utisak da ti se u prethodnom postu slučajno desilo da napišeš da se stepenovanje racionalnim brojevima radi pre uvođenja korena. Što se tiče zvanične definicije korena (ili bilo kog mat. pojma) zaista ne postoji ništa tipa: ISO Math 2006 Ja ni malo ne brkam cifru kojom se broj nula označava sa samim pojmom nule. Zapravo imam jednu nedovršenu raspravu sa Nedeljkom na tu temu Da li ti misliš da se može razumeti šta predstavljaju zapisi u kojima se javlja cifra nula a da se ne razume šta ta cifra označava? U mističkom smislu, za mene je 0=tao=celo, pa je 0 nekako sveobuhvatna i ako se to sme reći, najveća i nepromenljiva - otuda mi se valjda i sviđa šta je na tu temu mislio: Citat: John Wallis: It is curious to note that Wallis rejected as absurd the now usual idea of a negative number as being less than nothing, but accepted the view that it is something greater than infinity. Despite this he is generally credited as the originator of the idea of the number line where numbers are represented geometrically in a line with the positive numbers increasing to the right and negative numbers to the left. Dakle, "koliko" treba dodati npr. konačnom broju 1 da bi se dobila takva beskonačna 0? Konačno ili beskonačno? Sad se setih, postoji i jedna kratka priča Majstori lože - Ursule Legvin u zbirci Dvanaest četvrti vetra u kojoj se opisuje otkriće (i simbolika) nule i negativnih celih. Ursula je amater - pa ne očekujte bog zna šta... [ Farenhajt @ 18.09.2006. 12:44 ] @
Ala ste mu ga vi dali, ljudi... Svaka čast
Dakle, pitanje je da li ono što se, zbog jednostavnosti, tako i tako predaje osnovcima prihvatamo kao KONAČNU definiciju ili samo kao SUŽENJE nečega što se u svojoj celosti uči kasnije, u srednjoj školi. Slično pitanje: ako se jednačina napiše kao 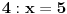 , onda nema rešenja, a ako se napiše kao , onda nema rešenja, a ako se napiše kao 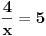 , onda ima, i to samo zato što u doba kad nam je definisan znak "podeljeno sa" (dvotačka) nismo znali da postoje i razlomci, nego samo deljenici, delioci, količnici i ostaci, svi iz skupa (pozitivnih!) prirodnih brojeva? Lično mi je to malo... hajd da kažem debilno , onda ima, i to samo zato što u doba kad nam je definisan znak "podeljeno sa" (dvotačka) nismo znali da postoje i razlomci, nego samo deljenici, delioci, količnici i ostaci, svi iz skupa (pozitivnih!) prirodnih brojeva? Lično mi je to malo... hajd da kažem debilno [ uranium @ 18.09.2006. 12:59 ] @
Pa ja sam već dosta puta napisao da se to tako uči i u srednjoj školi i na fakultetu - ako imate želju rado ću to dokumentovati. Nasuprot tome - niko ko zastupa drugu stranu nije ponudio ništa opipljivije od korisničkog interfejsa Mathematica-e
Da malo imitiram Nedeljka Da li vi uopšte znate kako se (čak i u slučaju standardne definicije) dokazuje egzistencija korena? [ Bojan Basic @ 18.09.2006. 13:26 ] @
Citat: uranium: Nasuprot tome - niko ko zastupa drugu stranu nije ponudio ništa opipljivije od korisničkog interfejsa Mathematica-e Dao sam jednom i ovaj link: http://mathforum.org/library/drmath/view/60847.html. Mislim da se ni mišljenje tih ljudi ne sme tek tako odbacivati. [ uranium @ 18.09.2006. 13:39 ] @
Čovek (koji se uzgred lažno predstavlja kao doktor) je rekao da bismo to mogli zvati korenom - s čime sam se odavno složio - ali naprosto to trenutno ne odgovara stanju stvari
[ uranium @ 18.09.2006. 13:52 ] @
...čak se i on na kraju ograđuje od svega:
Citat: "Doctor" Peterson: But we usually avoid this, since on one hand it is not necessary (roots being just a shorthand for reciprocal powers), and on the other hand it is potentially confusing (as we've just seen!). It's better to stick to exponential notation, apart from familiar cases like square roots. [ Bojan Basic @ 18.09.2006. 14:03 ] @
Ne bih baš toliko napadao čoveka zbog „lažnog“ predstavljanja — koliko ti imaš veze s uranijumom, toliko on ima veze s doktorom. :) Više puta me je Google doveo na taj sajt i stekao sam utisak da ljudi ne pričaju bez veze, pa sam ga zbog toga naveo.
Što se tiče ograđivanja, izraz „potentially confusing“ ne odnosi se na zbunjivanje o kom ovde pričamo (domen), već na to da se kod eksponencijalne funkcije razlomak okreće, a kod korenovanja ne (primer je dat ranije u tekstu), što se nekad može pomešati. [ Farenhajt @ 18.09.2006. 14:16 ] @
[ uranium @ 18.09.2006. 14:46 ] @
Ne bih da ljutim Farenhajta sa ovolikim skretanjem sa teme...ali:
@Bojan Basic: Ne treba ono shvatiti baš kao napad - više kao šalu, a evo i zašto. Ako neko radi na sajtu Ask Dr. Math, pa se još i potpisuje kao "Doctor" to bi trebalo da ostavi utisak da čovek izuzetno dobro poznaje materiju o kojoj priča. Kada sam prvi put naleteo na taj sajt mislio sam da se zaista radi o nekim doktorima, ali su me neke stvari brzo razuverile - kasnije sam u odeljku About Ask Dr. Math pročitao da se tu zapravo radi o studentima Swarthmore koledža. U nekoliko navrata sam im slao neka pitanja, iskreno tražeći bilo kakvu pomoć - pa makar i upućivanje na neku literaturu, članke - bilo šta, i šta misliš kakav sam odgovor uvek dobijao?! Nikakav. To što oni mogu nekome da odgovore - za toliko znam i sam. Ne mogu jednoznačno da odredim na šta si mislio kad si pominjao moju vezu sa "uranijumom" Uopšte nije važno šta ko smatra zbunjujućim - pitanje je bilo samo šta je opšteprihvaćena definicija - a tu su stvari kristalno jasne. Da postavim i ja jedno srodno pitanje: Može li neko reći nešto o etimologiji reči koren (u mat. smislu)? etymon=koren [ Bojan Basic @ 18.09.2006. 16:13 ] @
Citat: Ništa lično naravno, hteo sam da kažem da se ti na ovom forumu potpisuješ kao uranium iako sumnjam da si napravljen od uranijuma, takođe bi me vrlo iznenadilo ako bih saznao da je Farenhajt koji priča s nama otkrio temperaturnu skalu (ako sam pogrešio u vezi s vama dvojicom, izvinjavam se [ chupcko @ 18.09.2006. 19:12 ] @
[ Nedeljko @ 18.09.2006. 20:35 ] @
[ Cabo @ 18.09.2006. 21:10 ] @
Koliko ja znam, nula ne pripada skupu prirodnih brojeva. Mene su tako učili i u OŠ, i u gimnaziji, i na faksu...
[ uranium @ 18.09.2006. 21:14 ] @
@Nedeljko:
Nadam se da ćeš bar ti potkrepiti tvrdnje nekom validnom referencom mislim na te tvrdnje o ravnopravnosti zapisa Mada...kad malo bolje razmislim, ti si baš čuven po tome što (kad ti to odgovara [ uranium @ 18.09.2006. 23:40 ] @
Citat: Bojan Basic: Ništa lično naravno, hteo sam da kažem da se ti na ovom forumu potpisuješ kao uranium iako sumnjam da si napravljen od uranijuma, takođe bi me vrlo iznenadilo ako bih saznao da je Farenhajt koji priča s nama otkrio temperaturnu skalu (ako sam pogrešio u vezi s vama dvojicom, izvinjavam se [joke] da raspršimo svaku sumnju: uranium što se tiče Farenhajta - zaista sam čuo da umeju da podivljaju oko godišnjice... [/joke] Ozbiljno, može biti da sam malo preterao - izvinjavam se svim učesnicima u diskusiji - samo sam želeo da naglasim da osoba koja je ono napisala nije doktor matematičkih nauka. [ Farenhajt @ 19.09.2006. 01:20 ] @
Hajde da i ja raspršim sumnje: Nick mi samo indirektno potiče od Danijela Farenhajta, a direktno od romana Reja Bredberija Farenhajt 451
[ uranium @ 19.09.2006. 12:12 ] @
U prilogu ove poruke možete videti kako su definisani koreni (u jednom srednjoškolskom udžbeniku, u dva fakultetska udžbenika i na jednom fakultetskom kursu). Pri tom, prve dve definicije podrazumevaju da je indeks prirodan broj, dok druge dve isključuju broj 1 iz razmatranja.
Smem li se nadati da će sad i druga strana učiniti isto? Dajte neki dokaz - prihvatam i falsifikat [Ovu poruku je menjao uranium dana 19.09.2006. u 13:27 GMT+1] [ uranium @ 19.09.2006. 13:33 ] @
@chupcko:
Ona definicija iz Kurepine knjige me obavezuje da ti se izvinim Što se tiče one pevaljke [ chupcko @ 19.09.2006. 20:28 ] @
Pa eto, ja sam vise mislio o uvodjenju korena u osnovnoj skoli a ne na fax-u. Generalno i dalje smatram da celokupno gradivo matematike recimo na fax-u bi prezivelo i bez definicije korena :).
A generalno jedna od mojih ideja je i bila cisto racionalne prirode, ako je stepenovanje dovoljno, onda korenovanje mozemo da prepustimo samo za prirodne brojeve vece od 2, ali da ne tupim punooooooo. Sto se tice muzike, ko me zna, zna vec sta slusam a i sta sviram :). Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|