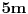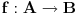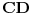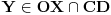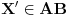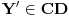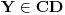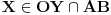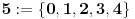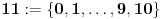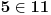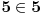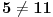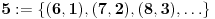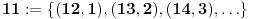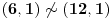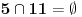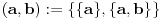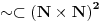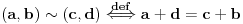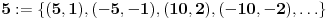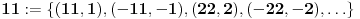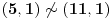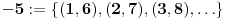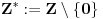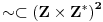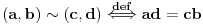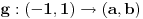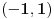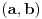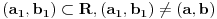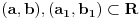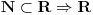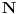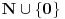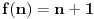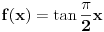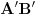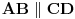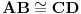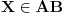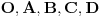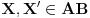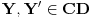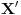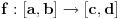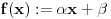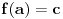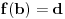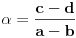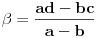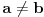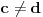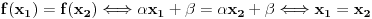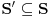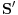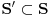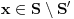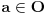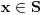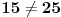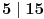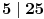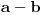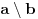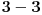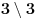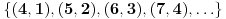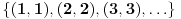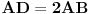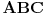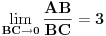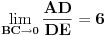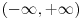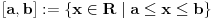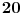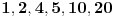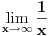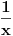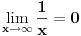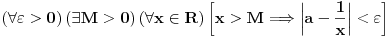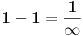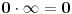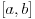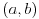|
|
[ galet@world @ 17.09.2006. 07:17 ] @
|
| Imam problema sa nekim prijateljima u pogledu terminologije ili možda definicije.
Rekao sam da se realni brojevi izražavaju količinom bezdimenzionalnih jedinica - da li je to pogrešno?
[Ovu poruku je menjao Bojan Basic dana 17.09.2006. u 14:11 GMT+1] |
[ uranium @ 17.09.2006. 07:23 ] @
@galet@world:
Ako za trenutak ostavimo po strani te bezdimenzionalne jedinice - na koji način definišeš količinu?
[ uranium @ 17.09.2006. 15:01 ] @
Da ne zaboravim:
to što radiš je zaista pogrešno - prijateljstvo je važnije od terminologije!  [ Mikky @ 17.09.2006. 16:04 ] @
Slazem se sa uraniumom...
Realni brojevi su unija racionalnih i iracionlnih brojeva... e sad diskusiju mozete da prenesete na ova druga 2 skupa, pre svega na iracionalne :)
[ galet@world @ 17.09.2006. 17:11 ] @
Ama bre ljudi, šta je s vama ili šta je samnom?
Ja sam samo usput pitao, a uranium mi na pitanje odgovara pitanjem.
Nisam čak mislio da se otvori tema po ovom pitanju, a eto Bojan je otvorio. Zašto?
Pa razmišljam - ili tamo gde sam ga postavio smetam, ili Bojan misli da ovom pitanju treba posvetiti posebnu pažnju.
U svakom slučaju pitanje je još uvek ostalo bez odgovora.
Uranijume moje prijateljstvo nije dovedeno u pitanje mojim odgovorom, bio on tačan ili ne.
[ uranium @ 17.09.2006. 17:36 ] @
Da se malo uozbiljim 
Uobičajeno je da se realni brojevi konstruišu pomoću tzv. Dedekindovih rezova - pri čemu se skup racionalnih uzima kao unapred dat.
Ako uzmemo u obzir postojeće definicije prirodnih, pa njima generisanih celih, pa njima generisanih racionalnih, pa njima generisanog skupa svih rezova racionalnih (pa na kraju čak i skupa svih rezova ovog poslednjeg skupa rezova  ) - vidimo da su realni brojevi zapravo jedna monstruozna struktura.
Upravo iz tog razloga, nakon što se konstrukcijom uverimo u postojanje realnih brojeva, uobičajeno je da se svi ti detalji konstrukcije zanemare i da se željena struktura uvede aksiomatski.
Dakle, ako gledamo ono što smo konstruisali - možemo slobodno reći da realni brojevi nisu unija racionalnih i iracionalnih, za razliku od situacije sa aksiomatski zadatim strukturama 
Konstrukcija o kojoj govorim ( Dedekindovi rezovi) može se videti npr. u knjizi Uvod u matematiku : skupovi-strukture-brojevi, Svetozar Kurepa, Tehnička knjiga, Zagreb 1975.
Sama ideja je izuzetno jednostavna, ali je količina detalja relativno velika.
Ako bude problema sa nabavljanjem pomenute knjige, smisliću već nešto  @galet@world:
@galet@world:
Meni se učinilo da je tvoja definicija nekako prazna (iako ima onaj uzbudljiv deo sa bezdimenzionalnim jedinicama) - pa sam prosto želeo da mi pojasniš malo na koji način bi recimo poredio te količine, da li bi postojali različiti realni brojevi i tome slično - jednom rečju da se ispita da li je definicija korektna.
Što se tiče one opaske o prijateljstvu, izvinjavam se ako je zvučala grubo, ali namera je bila potpuno suprotna. [ Bojan Basic @ 17.09.2006. 17:49 ] @
Ne bih rekao, galet@world, da tamo „smetaš“, već se tamo jednostavno govori o drugim stvarima koje nemaju mnogo veze s ovim pitanjem, i zato sam ga premestio u zasebnu temu.
Što se tiče tvog pitanja, to što si ti rekao nije definicija realnih brojeva. Oni se mogu definisati na više načina, od kojih je verovatno najpoznatiji onaj preko Dedekindovih rezova, što je uranium napisao. Ipak, da bismo bolje razumeli tvoj predlog definicije, neophodno je da objasniš neke stvari. Dakle, ako realne brojeve želiš da definišeš kao količinu bezdimenzionalnih jedinica, moraš reći i šta je za tebe „količina“ — u suprotnom definicija nije kompletna.
Ne znam zašto imaš utisak da su svi protiv tebe (ili možda grešim?), ali nije tako, svi su ovde dobrodošli (sve dok se ponašaju u skladu s pravilima foruma i elementarne kulture).
[ galet@world @ 17.09.2006. 22:11 ] @
Ma nisam ja toliko svilen i uopšte ne mislim da je bilo ko protiv mene, taman posla.
Ako saopštim neki realan broj bilo da sam ga napisao ili izgovorio onda je on strogo određen i ne treba mu nikakvih dodataka. Na primer broj 2,71828...
Pitanje je: čime je izražen taj broj?
Očigledno je da taj broj sadrži dve jedinice, sedam desetih delova jedinice, jedan stoti deo jedinice i t. d.
Svaki broj kaže ustvari koliko ima jedinica zar ne?
E sad je problem u reči "koliko" jer ona znači količinu. Ako količinu izrazim brojem, a broj količinom onda se vrtim u krug i nisam ništa uradio.
Dakle količinu bi trebalo izraziti nekako drukčije, bar mi se čini da na to mislite.
Za sad mi nešto odgovarajuće ne pada napamet.
Ali da nastavim. Po čemu se neki broj razlikuje od drugih? Pri tom ne mislim na računsku razliku nego na različitost koja kaže po čemu je on drukčiji od drugih brojeva. Šta ga čini drukčijim?
Po čemu se na primer razlikuje broj 5 od broja 11?
[ Bojan Basic @ 17.09.2006. 22:59 ] @
Citat: galet@world:
Po čemu se neki broj razlikuje od drugih? Pri tom ne mislim na računsku razliku nego na različitost koja kaže po čemu je on drukčiji od drugih brojeva. Šta ga čini drukčijim?
Po čemu se na primer razlikuje broj 5 od broja 11?
Ako brojeve definišemo pomoću Dedekindovih rezova onda postoji jednoznačna korespondencija između rezova i brojeva. Dakle broj  razlikuje se od broja 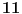 zato što se razlikuju i odgovarajući rezovi. Možda ćeš sad pomisliti da isto možemo reći i za „količine“, ali tu je greška. Prilikom definicije rezova mi još uvek nemamo predstavu o realnim brojevima, dok mi se čini da tvoja količina podrazumeva realne brojeve. Drugim rečima, kao što si i sam rekao, vrtimo se u krug.
Da probamo i ovako. 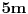 jednako je  „količina“ dimenzionalne jedinice metar, odnosno (broj) pet metara. Ovo me opet navodi na pomisao da je tvoja „količina“ zapravo samo drugi naziv za broj. [ galet@world @ 18.09.2006. 08:47 ] @
Citat: uranijum: Sama ideja je izuzetno jednostavna, ali je količina detalja relativno velika.
Ako bude problema sa nabavljanjem pomenute knjige, smisliću već nešto
Nisam uspeo da nađem tu knjigu - ima li kakva druga?
[ uranium @ 18.09.2006. 10:46 ] @
Ima: Principles of Mathematical Analysis, W. Rudin - a ako bude problema sa nalaženjem i te knjige, pošalji mi privatnu poruku pa ćemo to rešiti.
A ako ipak mora da bude na srpskom/hrvatskom - mogu da fotografišem tih nekoliko stranica i da ih postavim negde (ako obećaš da ćeš me posećivati na robiji  )
Do tad, pogledaj:
Dedekind cut
planet Math: Dedekind cuts
[Ovu poruku je menjao uranium dana 18.09.2006. u 13:29 GMT+1][ galet@world @ 18.09.2006. 15:37 ] @
Obećavam, kaži mi samo koje cigarete pušiš!
[ uranium @ 18.09.2006. 17:33 ] @
Dobro! Obeć'o si! 
Evo u prilogu imaš jednu "lite" verziju - uz povremeno zumiranje može da se čita.
Ako je rezolucija suviše niska, ili ako sam nešto zabrljao - reci pa ću popraviti.
arhiva je šifrirana[ Nedeljko @ 18.09.2006. 20:52 ] @
Bilo bi lepo kada bi nas galet@world, pošto prouči problematiku, podučio koliko je cos 0o i koliko je 0/0.
[ galet@world @ 18.09.2006. 22:15 ] @
uranijume ovo ne može da se čita - nije u pitanju rezolucija nego znakovi.
Nedeljko opet si pogrešio (verovatno si zaboravio) - nije bio u pitanju kosinus od nula stepeni nego kosinus od nule
[ uranium @ 18.09.2006. 22:23 ] @
Koji znakovi?!?  [ galet@world @ 19.09.2006. 06:01 ] @
Citat: )Â�¨Å"6iÉn½�ð–IJ¾�Gh¦Æ\öÌ*O*�R 7s·‘Æ�Lyd°B¥ƒ‘¯�ðô
…‰ÔûtÖݪ¿6ÅÝj�¬£Ä¬�`ü¶÷ƒ3WÀ8üp3º�mȺÛ<¤ìš+mC^ÄR8á\ù
ËÍ´ž�Ô?ô£¾oÐed©?�8r¯Õª;œƒó�Èy6©«¬l¦?Óô<¨�!¤yŒ=]fÍ«¯Q‚xæ>žéKµÈµ@i�\UeV|±�ñ2#(0�ÝyGi|oQD{/ÇšÎÊ:¸!Ã�BåóÔG>kIŒ¥Ï…žb*åKŸCäsŽUý÷žÈêf–¾¥5g®žJ��®Û‡û³°Ú�|d�Ð�‚ê`„zxpï÷å¼#Eê¤ÀÓÞæ~ù;”+��€€„>eç&ÛœªHÊ®¢—:�&š@<”ðG˜Ÿl¸•¹P
œ~�몹úT›»Šk�£Å@u(÷�í\�·ä&T•’vð&r�h4óH|D£j\Þ�ýIËݺ�Âb�gP–<õ¡¸�r��yEÎ��b
ørÍÁ©š-÷ilE
r^µ�+�Å‘€ÿiŽª�§f�O�%nVMI�î�›…]Hƒ\�9�Î2Ž.aV*>÷ºzø»�×CÅ¢OžP›;hÛÔTE�eŸqÖ�Z÷ž�Yu#:�;;…]^MYŒ�Ü+�^À°ð¹ä‹/,‡þN÷ûs¿·
*�e¥(¾ÿTOM7Flæeƒ¼3¤¬Ø£`çµ×1��/�}�ØKP”}V�v‹ö…k��“âTE�"ü*O§K*BŠµÒÿ%Ž»1°{™}�O ;±í�lÆ>7|o+¥ëTk“�@œÙP�5)ŒGÃÅ$Eµ·��ÓJ�ÏÒ3`˹–É��þäýnO-xçÈ��KÒ`‘Ã%3ÔÂRgÖy3!Èñœ Rÿ¸1^æÚHá� �¥]<�Ù”Kñèþž¡Úõ¢¾ŠM\ñº�ô0�¨�s��R ��¸‡I؈têhMÁõ…º=‚Ë�kߟ˜^dâ¬�ô±ºýá—�GŸÄSÂV˜ÂÊrß”ÓÆùΡ½–À©‘ÖÅ_©i8XYïêŠN�P=ï" � ¿°Ð"Ùä[³îó¤ß2r#èÕ‘=e~���ljb²ðÓ¤Qq¨=� ¾+µ¡�ŒÜtÝ£øŒBWöE*ËÔ�å@;%,è�›�¦�€\¦!˜ê�fc�¥Í.�™’ZœaS�XÒÿµÝáÖ�s
�¡AgûdJôÄžf¬†Dþßתi�eĩe.JÙED�œQéß¡§î�/¹JâïºÆ$ÿ´{iÀi醮À=Eë—Âf0»™K˜�ëãù…/z@+¹Òh?0¬�ü#צ¸�)�àÄwí�¤c¤�õŒ.DçÛý��ïZèl��–9³7§�b5Y«¥0FÈ)/âÜËíÑÜ]�u(þ`@¯lV9�&ˆ©mµŸÓ,Ê�ýc³Ñ-F÷=d§¯ã �-[f±Qˆ
´ÜH#Ž¼nasn›åkóp�ÌxŠê�ìÏ;�¯]Ö��öÝpÔ3@¨ÚÅ�™âd(E¢$8>ö€æÞp(1‹{¸`¥
Evo tih znakova [ uranium @ 19.09.2006. 06:55 ] @
Sada moram da postavim neka (glupa) pitanja.
Da li si raspakovao arhivu?
Ako jesi - u njoj bi trebalo da se nalazi nekoliko slika u .jpg formatu.
Zanimljivost: kada arhivu otvorim iz Notepad-a mogu da pronađem sekvencu koju si citirao 
Dakle, da bi raspakovao fajl - dovoljno je da imaš neki WinZip ili RAR (a ako se ne varam mislim da i sam Windows može da ti raspakuje .zip arhivu) - i da uneseš šifru koju si dobio.
Ako ti je sve ovo problematično ostavi mi neku e-mail adresu (najbolje preko privatne poruke - ako ti je to dopušteno) pa ću ti poslati nezapakovano... [ galet@world @ 19.09.2006. 15:09 ] @
Uranijume uspelo je. Hvala ti mnogo.
[ Mikky @ 19.09.2006. 16:18 ] @
Koja je sifra za arhivu?
[ uranium @ 19.09.2006. 16:30 ] @
Ah...pa koliko se sećam ti se nisi prijavio na listu budućih posetilaca...  proveri privatne poruke
proveri privatne poruke[ Nedeljko @ 20.09.2006. 15:54 ] @
Citat: galet@world: Nedeljko opet si pogrešio (verovatno si zaboravio) - nije bio u pitanju kosinus od nula stepeni nego kosinus od nule
Svejedno, uživaćemo u tvojim časovima. [ galet@world @ 20.09.2006. 21:50 ] @
Mogao bi i ti ponekad da nešto pametno kažeš u pauzi između grešaka.
Ti znaš da ja nisam matematičar, pa bih te zamolio da mi objasniš bijekciju.
Kažu da se pomoću bijekcije može dokazati da dve različite dužine imaju jednak broj tačaka.
Možda bi to mogao da nacrtaš.
[ Bojan Basic @ 20.09.2006. 22:36 ] @
Citat: galet@world:
Mogao bi i ti ponekad da nešto pametno kažeš u pauzi između grešaka.
Galet@world, ovakvim komentarima nema mesta, a posebno ako se ne razumeš mnogo u stvari o kojima želiš da raspravljaš (kao što si sam rekao). Ovakvo ponašanje više neću sankcionisati.
Uzgred, možda bih mogao da ti kažem da je 0° = 0.
Definiciju bijekcije pogledaj bilo u kom udžbeniku koji se time bavi, pa ako ti nešto ne bude jasno onda možeš da pitaš, a ne da tražiš da ti neko priča sve iz početka. [ uranium @ 21.09.2006. 00:10 ] @
Citat: Bojan Basic:
Ovakvo ponašanje više neću sankcionisati.
Auh - izgleda da je reč sankcija kontranim (ako se uopšte tako kaže  )
Vidim da je moje neodgovorno ponašanje (u poslednjih nekoliko dana) ostavilo traga - uz izvinjenje svima, obećavam da ću to popraviti.
Evo za kaznu (da ne kažem sankciju  ):
@galet@world :
Za preslikavanje 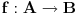 kažemo da je bijekcija ako:
• svakom elementu skupa  pridružuje tačno jedan element skupa 
• (injektivnost): različitim elementima skupa  pridružuje različite elemente skupa 
• (surjektivnost): svaki element skupa  je pridružen nekom elementu skupa  prvi uslov se uvek podrazumeva kad pričamo o jednoznačnim funkcijama - ali sam ga naveo za svaki slučaj
prvi uslov se uvek podrazumeva kad pričamo o jednoznačnim funkcijama - ali sam ga naveo za svaki slučaj
Što se tiče zadatka sa dužinama - trik je u centralnoj projekciji:
[att_img]
Vidimo da će za svaku tačku  duži  postojati tačno jedna tačka  duži 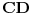 takva da 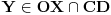 .
Na osnovu konstrukcije je jasno da će se svaka tačka 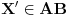 različita od  preslikati u neku tačku 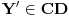 različitu od  .
S druge strane bilo koja tačka 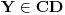 je slika tačno jedne tačke 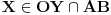
[ Bojan Basic @ 21.09.2006. 00:38 ] @
Citat: uranium:
Auh - izgleda da je reč sankcija kontranim (ako se uopšte tako kaže  )
Još malo oftopika, kao da ga već nema dovoljno (ma gde su ti moderatori?!). 
Imenica sankcija zaista ima dva značenja: kazna i odobrenje, ali to se ne može reći za glagol sankcionisati, koji je vrlo jednoznačan:
Rečnik Matice srpske, peti tom:
Citat: sankciònisati, -išēm svrš. i nesvrš. = sankcionirati.
...
sankcionírati, -ònīrām svrš. i nesvrš. = sankcionisati dati, davati sankciju (1), odobriti, odobravati, potvrditi, potvrđivati.
...
sànkcija ž (gen. mn. sȁnkcījā) lat. 1. a. potvrda zakona od strane državnog poglavara. b. odobrenje, potvrda potrebna da bi nešto postalo punovažno.
Vujaklija:
Citat: sankcionisati (lat. sanctus svet, fr. sanctionnet) jedan zakon učiniti svetim i neprikosnovenim, potvrditi, odobriti; nešto utvrditi, učiniti zakonom, dato čemu zakonsku silu.
Eto, ako nekog zanima šta znači sankcionisati, neka slobodno dođe kod nas na forum Matematika.  Za radoznale: jesam namerno upotrebio taj glagol očekujući da izazove sličnu reakciju, nešto sam večeras raspoloženiji za raspravu nego inače.
Za radoznale: jesam namerno upotrebio taj glagol očekujući da izazove sličnu reakciju, nešto sam večeras raspoloženiji za raspravu nego inače.  [Ovu poruku je menjao Bojan Basic dana 21.09.2006. u 01:55 GMT+1]
[Ovu poruku je menjao Bojan Basic dana 21.09.2006. u 01:55 GMT+1][ uranium @ 21.09.2006. 05:29 ] @
U nekoj od prethodnih poruka galet@world je postavio zanimljivo pitanje: u čemu se razlikuju brojevi 5 i 11?
Ako ove brojeve shvatimo kao prirodne, po (jednoj) definiciji bi bilo:
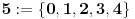 i 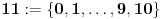 pa odmah vidimo da recimo važi 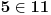 ali ne važi npr. 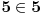 pa je 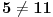 .
Ako te iste brojeve shvatimo kao cele, po uobičajenoj definiciji bilo bi:
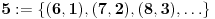 i 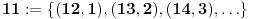 pa kako recimo 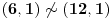 vidimo da je 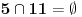 pa opet 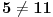 .
Napomena #1: uređeni par se definiše kao 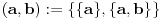 Napomena #2:
Napomena #2: relacija 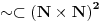 je ovde definisana sa 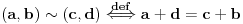
Ako date brojeve shvatimo kao racionalne, po standardnoj definiciji bi bilo:
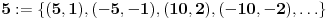 i 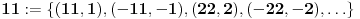 pa zbog 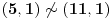 sledi 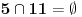 a otuda i 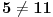 .
Napomena #3: ne treba brkati iste oznake koje se javljaju sa leve i desne strane definicione jednakosti npr. oznaka  sa leve strane je racionalan broj koji tek uvodimo a ista ta oznaka na desnoj strani je ceo broj koji je uveden ranije.
Napomena #4: primera radi 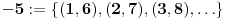 i analogno za ostale negativne...
Napomena #5: ako uvedemo oznaku 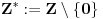 relacija 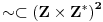 je u ovom slučaju definisana sa 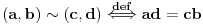 .
Ako date brojeve shvatimo kao realne dokaz različitosti je još lakši...ostavljam da ovo uradi galet@world  sve je moglo mnogo lakše da se dokaže potapanjem odgovarajućih struktura, ali eto...
sve je moglo mnogo lakše da se dokaže potapanjem odgovarajućih struktura, ali eto... 
Poenta cele ove priče je u tome da ako baratamo sa konstruisanim brojevima - možemo u konačno mnogo koraka proveriti da li su dva data broja jednaka.
ovde, istina, ima nekih detalja i ograničenja koja bi valjalo precizirati, ali to tek ako bude zahteva 
Ako radimo sa aksiomatski uvedenom strukturom - pitanje je nemoguće postaviti bez ponavljanja (na neki način) opisanih konstrukcija...
Priznajem da ovim nije sve rečeno i da je karakterizacija npr. prirodnih, bar što se mene tiče, i dalje obavijena velom magle  [Ovu poruku je menjao uranium dana 21.09.2006. u 16:56 GMT+1]
[Ovu poruku je menjao uranium dana 21.09.2006. u 16:56 GMT+1][ galet@world @ 21.09.2006. 06:55 ] @
Citat: galet@world: Mogao bi i ti ponekad da nešto pametno kažeš u pauzi između grešaka.
Bojane, potpuno se slažem da ne treba tolerisati tekstove ovakve vrste, ali da li se ti slažeš da isto tako ne treba tolerisati izazove?
Citat: Bojan Basic: Uzgred, možda bih mogao da ti kažem da je 0° = 0.
Hvala! Moram, izgleda, da budem vrlo oprezan. Ovo bih hteo da kažem - ako od nekog ugla oduzmeš isto toliki ugao onda dobiješ nulu t. j. ne ostane ti ništa - nema više ugla. Ugao ne postoji!
Kako onda može postojati kosinus od nepostojećeg ugla?
Ako nema ugla, onda valjda nema ni kosinusa.
Ne znam zašto ovakva pitanja nekog iritiraju i šta je tu nedopustivo.
Uranijume, hvala ti na pomoći i naročito na tvom korektnom stavu.
Bijekcija mi se učinila vrlo interesantnom za slična pitanja kao ovo gore, ali odustajem od zaista interesantnih pitanja i zaključaka, jer ne mogu da postupam suprotno uputstvu koje sam dobio.
Nisam matematičar pa verovatno ni meni ni mojim pitanjima nije mesto ovde. [ Farenhajt @ 21.09.2006. 06:56 ] @
Kad smo kod aksiomatike realnih brojeva, ne zaboravimo ni uraniumovu aksiomu singulariteta: 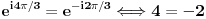  [Ovu poruku je menjao Farenhajt dana 21.09.2006. u 10:51 GMT+1]
[Ovu poruku je menjao Farenhajt dana 21.09.2006. u 10:51 GMT+1][ uranium @ 21.09.2006. 07:33 ] @
@Farenhajt:
Tu quoque Brute mi fili?!? 
Samo da znaš da je to mnogo jaka aksioma - iz nje sledi sve što poželiš!
koristiti oprezno  @galet@world:
@galet@world:
Mislim da bi bila šteta da sad odustaneš.
To što eventualno nisi upoznat s nekim mat. teorijama može da ti bude prednost u smislu da možeš, neopterećen tuđim idejama, da misliš o problemu hladne glave i da uočiš nešto što svi mi previđamo.
Neki matematičari se ponekad zanesu misleći da se matematika bavi otkrivanjem istine pa da su samim tim neki teorijski okviri dati jednom za svagda - srećom (po matematiku) to nije tako.
Razmisliću malo o ovom novom problemu...
[Ovu poruku je menjao uranium dana 21.09.2006. u 15:07 GMT+1]
[ Bojan Basic @ 21.09.2006. 13:07 ] @
Citat: galet@world:
Bojane, potpuno se slažem da ne treba tolerisati tekstove ovakve vrste, ali da li se ti slažeš da isto tako ne treba tolerisati izazove?
Ne treba tolerisati izazove?! Kad god neko postavi zadatak ovde na forumu koji ne znam da rešim na prvi pogled, to smatram izazovom. Treba li onda da brišem takve stvari (verovatno s obrazloženjem: „Ja ne znam to da rešim“)?
Citat: galet@world:
Ovo bih hteo da kažem - ako od nekog ugla oduzmeš isto toliki ugao onda dobiješ nulu t. j. ne ostane ti ništa - nema više ugla. Ugao ne postoji!
Ko zna pre koliko vekova nula je prestala da bude „ništa“ i postala je samo još jedan broj s kojim možeš raditi sve što i s ostalim brojevima.
Citat: galet@world:
Nisam matematičar pa verovatno ni meni ni mojim pitanjima nije mesto ovde.
Vidi, ako ne znaš i želiš da naučiš — to je svakako u redu i vrlo pozitivno; ako znaš i hoćeš drugima da pomogneš — i to je naravno u redu; ali ako nisi stručan u oblasti o kojoj se diskutuje (kao što sam kažeš) onda mislim da bi bilo dobro da prihvatiš objašnjenja onih koji su stručniji i više znaju od tebe, a čak i ako se s tim ne slažeš nipošto nemaš pravo da nekoga vređaš, već samo da kulturno izneseš argumente koji brane tvoj stav. Opomenuo sam te, ako prihvatiš opomenu i nastaviš da kulturno diskutuješ sve može biti potpuno zaboravljeno, zlopamtilo nisam. [ galet@world @ 21.09.2006. 19:58 ] @
Ne Bojane - to nije bio izazov te vrste o kojoj ti pričaš, ne mogu verovati da to ne vidiš, ali ako zaista ne vidiš onda pitaj autora izazova.
Ako poslušam uranijuma ( još sam u dilemi) i vratim se ovde, mislim da mogu pokazati da nula može biti i nešto i ništa.
Nikada, ama baš nikada, nisam prenosio raspravu na lični plan, ako nisam bio bez razloga uvređen.
Prenošenje rasprave na lični plan smatram nedostatkom kulture, odnosno primitivizmom.
[ Mlatko @ 22.09.2006. 00:50 ] @
Mozda malo zadirem u offtopic, ali cisto ne mogu a da se ne umijesam:)..
Citat: uranium:
Što se tiče zadatka sa dužinama - trik je u centralnoj projekciji:
.../cut/...
Na osnovu konstrukcije je jasno..
.../cut/...
S druge strane bilo koja tačka 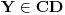 je slika tačno jedne tačke 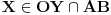
Jel se jos nekome cini ovakav nacin dokazivanja malo "manjkavim", ili sam to ja previse
paranoican?:)
Npr. pogledajmo zadnju, gore citiranu tvrdnju. Na osnovu cega zakljucujemo da je bilo koja tocka 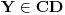 slika tocno jedne tocke 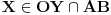 ?
Ako je zbog toga sto smo prethodno rekli da se svaka tocka iz  preslika u razlicitu tocku iz 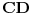 , kako znamo da su bas sve tocke iz 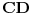 pogodjene ciljajuci zelenom zrakom kroz sve tocke iz  ?
No cak i ta pretposljednja tvrdnja, u kojoj se tvrdi obrnuto, djeluje diskutabilno, jer se nekako previse oslanja na "ociglednost", a znamo da u matematici ne bi smjelo biti takvih zakljucaka.
Jer inace meni zadnja tvrdnja izgleda jednaka ovoj: bilo koja tocka 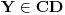 slika tocno jedne tocke 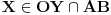 zato sto eto ja upravo kazem da je to tako :).
Volio bih vidjeti na sto se to tocno pozivamo kad napisemo tvrdnje poput tih?
(Napomena: posto prvi put ulazim u neku diskusiju, da jasno kazem kako mi nije namjera nista spocitati Uraniumu, dapace, volim citati njegove lijepe, leprsave i iscrpne odgovore :), te ovo pisem i pitam iz iskljucivo "matematickih" razloga)
Uglavnom, uvijek su me u slicnim dokazima smetale sintagme: "na osnovu konstrukcije zakljucujemo.." , "ocigledno je da.." i sl. Meni to izgleda nekako manjkavo, jer imam osjecaj da najcesce "zakljucujemo" ono sto nam pase da zakljucimo:).. Hocu reci, kako u tim dokazima nekako nedostaje matematicnosti tipa: na osnovu teorema tog i tog zakljucujemo to i to.
Evo da budem jasniji, galet@world je trazio rjesenje sljedeceg:
Citat: galet@world:
Kažu da se pomoću bijekcije može dokazati da dve različite dužine imaju jednak broj tačaka.
Meni se svidja recimo ovakvo dokazivanje:
(vjerojatno postoji i mnogo koncizniji nacin, ali eto ja sam to sklopio nekako ovako: )
Uzmemo li da postoji jednoznacna korespodencija izmedju zatvorenih intervala iz skupa realnih brojeva i duzina na pravcu, problem se moze svesti na dokazivanje da su svaka dva zatvorena intervala ekvipotentna:
Uzmemo proizvoljni interval 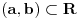 . Definiramo 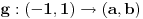 sa 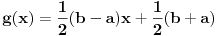 .  je bijekcija (lako se pokaze). To znaci da su 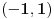 i 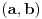 ekvipotentni
(dva skupa su ekvipotentna ako postoji bijekcija izmedju njih).
Kako je 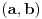 bio proizvoljan, to je dakle (-1,1) ekvipotentan i s bilo kojim 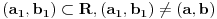 .
Kako je relacija "biti ekvipotentan" relacija ekvivalencije, to zbog njene simetricnosti i tranzitivnosti zakljucujemo da su bilo koja dva intervala 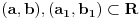 medjuosbno ekvipotentni.
Ovo je bio dokaz za otvorene intervale. Za prosirenje na zatvorene, trebamo pokazati da je proizvoljni (a,b) beskonacan skup, pa cemo se pozvati na teorem koji kaze da je
svaki beskonacan skup ekvipotentan uniji tog skupa i nekog konacnog skupa,
a taj konacni dodatak ce biti skup koji se sastoji od rubnih tocaka a i b, pa cemo dakle dobiti da je svaki (a,b) ekvipotentan s [a,b]. I na kraju primjenom simetricnosti i tranzitivnosti ekvipotentnosti, te uz vec dokazano za otvorene intervale, ustvrditi da su bilo koja dva dva zatvorena intervala ekvipotentna:
Pa pokazimo da je (a,b) beskonacan:
Imamo najprije: 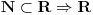 je beskonacan
(svaki nadskup beskonacnog skupa je beskonacan)
(a 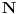 beskonacan jer udovoljava definiciji beskonacnosti: skup X je beskonacan ako je ekvipotentan uniji tog skupa i skupa koji sadrzi element koji nije iz X. Npr. imamo da je 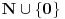 ekvipotentan skupu 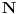 jer izmedju njih postoji bijekcija 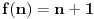 . )
No 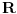 je ekvipotentan s (-1,1), jer postoji bijekcija izmedju njih: 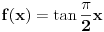 , dakle (-1,1) je takodjer beskonacan, a onda je takav i (a,b) jer smo prije ustvrdili da je ekvipotentan s (-1,1).
Dakle (a,b) je beskonacan.
Napravimo sad uniju 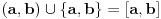 . To je unija beskonacnog i konacnog skupa, koja je, prema gore pomenutom teoremu, ekvipotentna skupu (a,b). Dakle [a,b] je ekvipotentan (a,b). Kako to vrijedi za proizvoljne a i b, to, visekratnom primjenom simetricnosti i tranzitivnosti relacije "biti ekvipotentan", slijedi da da su proizvoljna dva zatvorena intervala ekvipotentna.
Eto, ispade malo preopsirno, ali nadam se da je jasno sto sam htio pitati.. (ako nije, pogledajte recenice u prvom dijelu posta na cijim krajevima stoje upitnici :) )
[Ovu poruku je menjao Mlatko dana 22.09.2006. u 03:46 GMT+1][ uranium @ 23.09.2006. 15:59 ] @
@Mlatko:
Hajde prvo da vidimo šta je to toliko čudno kod one konstrukcije i na šta/koga se ja to pozivam 
Vodeći se onom čuvenom (Konfučijevom?) izrekom - "Slika vredi hiljadu reči" - nisam ni napisao neke pretpostavke jer se one "vide" sa slike - ali eto, neko više voli tih hiljadu reči  (koje se, istina, zapisuju pomoću nekoliko hiljada manjih slika, ali dobro de...  )
Dakle, izabrane su dve proizvoljne nepodudarne duži 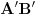 i 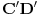 i nekim izometrijama su prevedene u duži  i 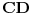 respektivno, tako da se prave 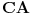 i 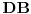 seku u nekoj tački  takvoj da su (nedegenerisani) trouglovi 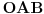 i 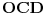 iste orijentacije - ovo je uvek moguće izvesti jer duži  i 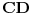 možemo birati tako da važi 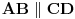 (a da nisu sve tačke kolinearne) a zatim upotrebiti teoremu koja kaže: 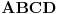 je paralelogram akko 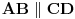 i 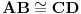 .
Proizvoljnu tačku 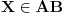 prevodimo u tačku 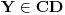 tako što pronalazimo tačku preseka prave 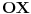 sa duži 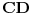 . Kako znamo da taj presek uvek postoji i da je jedinstven? Za egzistenciju, dovoljno je da se pozovemo na teoremu koja kaže:
Neka je zadat konveksan ugao 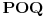 . Svaka poluprava koja sadrži teme  , nalazi se u unutrašnjosti ugla 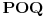 akko seče otvorenu duž 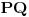 .
Jedinstvenost:
ako bi bilo više od jedne presečne tačke, onda bi imali kolinearnost tačaka 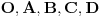 što bi protivrečilo njihovom izboru.
Pogledajmo zašto se različite tačke 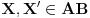 slikaju u različite tačke 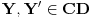 .
Ako bi se i  i 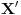 slikale u  imali bismo da 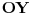 seče  u dve različite tačke - a to bi opet dovelo do kolinearnosti svih posmatranih tačaka.
Surjektivnost dokazujemo ponovnim pozivanjem na poslednju navedenu teoremu.  O vrstama dokaza:
O vrstama dokaza:
Ti sad ne možeš biti zadovoljan ni ovakvim dokazom. Ali šta da uradim? Da krenem da dokazujem i teoreme na koje sam se pozivao, pa zatim i teoreme na koje se budem pozivao u dokazu onih prethodnih i tako sve dok ne stignem do aksioma? I kud onda? Na samom kraju morao bih da priznam nešto što sam mogao da priznam i na početku - nemoguće je sve dokazati - moramo se osloniti na intuiciju i prihvatiti tu i tamo po neku očiglednost.
S druge strane, potpuno ista (geom.) teorija se mogla dobiti i od nekog nestandardnog skupa aksioma. Time bi neki dokazi bili lakši a neki teži. I što bi jedna očiglednost bila bolja od neke druge? Da li polako uviđaš relativnost svih dokaza?
To nažalost nije sve - ključni problem uopšte nije matematičke prirode.
Problem je u svesti i komunikaciji tj. pokušaju prenošenja "sadržaja" svesti drugima.
Evo kakvo je moje iskustvo.
Zamislimo da sam uočio neku pravilnost  i posle nekog vremena uspeo da dokažem s tim u vezi neko tvrđenje  . Moja svest je time izmenjena i od tog trenutka ja postajem ubeđen da važi  . Ali šta je to što me je ubedilo? Da li je to detaljan dokaz koji sam izveo? Nije! Ključan je bio neposredan intuitivan uvid u tu pravilnost - bez toga ne bi bilo ni dokaza. Ta "misaona slika" je zapravo "nevidljivo tkanje" dokaza. Neposredan uvid u nešto, naspram čitanja dokaza je kao razgovor s nekim licem u lice, naspram gledanja nečije crno-bele fotografije.
Ukoliko je dokaz dovoljno složen, čovek koji bi ga čitao a ne bi imao odgovarajuću "sliku" u glavi, ne bi mogao ni da prati dokaz pa ma koliko dokaz bio "usitnjen".
Da pokušam da dam još jednu analogiju: zaustavi me čovek na ulici i pita kako da stigne na neku obližnju lokaciju. Ja mu pokažem rukom gde treba da prođe, on uoči šta mu pokazujem i krene sam. Zamislimo sad da treba da nateram robota (koji nema odgovarajuće senzore) da ode na tu istu lokaciju. Morao bih da odem sam umesto njega, premerim sva potrebna rastojanja, da razmislim o eventualnim preprekama na koje bi mogao da naiđe, smislim odgovarajuću strategiju... i najzad dam mu izuzetno precizne i opširne instrukcije kad šta da uradi. Na kraju, da li bi robot uopšte znao šta je uradio i zašto?
Do sad sam isticao neke razlike,..ali ako pogledamo jedan "elementaran" korak tog velikog dokaza - zapažamo sličnosti sa onim neposrednim uvidima. Pa se ispostavlja da se u suštini nismo oslobodili pozivanja na očiglednost...
Šta sve ovo znači? Da li su nam potrebni formalni dokazi? 
Mislim da ipak jesu, ali o tom drugom prilikom - da ne preterujem...
[ uranium @ 24.09.2006. 12:17 ] @
@Mlatko:
Zaboravih da pomenem:
mogao si direktno da dokažeš to što si hteo uvodeći f-ju:
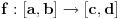 definisanu sa 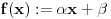
Iz uslova 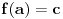 i 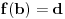 dobijamo sistem po  i  pa zatim i rešenja:
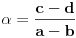 i 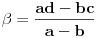
Pošto je 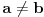 i 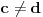 imamo da je 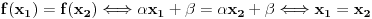 pa je f-ja injektivna.
Surjektivnost sledi iz:
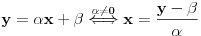 i 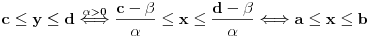
[ galet@world @ 27.09.2006. 14:12 ] @
Citat: Uzgred, možda bih mogao da ti kažem da je 0° = 0.
Tvrdim da nije isto ako neki broj ima dimenziju i ako je nema. Tu ne može stajati znak jednakosti.
Citat: Ko zna pre koliko vekova nula je prestala da bude „ništa“ i postala je samo još jedan broj s kojim možeš raditi sve što i s ostalim brojevima.
Reči “prestala” i “postala” pretpostavljam da ovde verovatno ne treba tumačiti u nekom matematičkom smislu?
U prvom citatu “crvena” reč “ti” je suvišna, ovo kažem u najboljoj nameri želeći da se rasprava prenese isključivo na temu, a da autore po mogućnosti uopšte ne pominjemo ni na koji način. Time ćemo hteli to ili ne izbeći lične sukobe kojima ovde nije mesto i koji ne doprinose rešavanju i objašnjavanju konkretnih problema. Ja ovim ne propisujem način raspravljanja (jer to, naravno, i ne mogu) nego samo predlažem – pa ako predlog valja trebalo bi ga i primeniti. Odstupanje od ovog pravila poželjno je samo u smislu poboljšanja “atmosfere” na forumu.
Što se tiče prošlih nepotrebnih ličnih sukoba – predlažem ovu krilaticu “bilo pa prošlo!”. Zlopamtilo ne treba biti.
Evo sad i nekih mojih “heretičkih” razmišljanja o nuli:
1. Postoji pozitivna nula koja označava principijelno postojanje nečega što ima
dimenziju.Takva nula ima dimenziju i sa njom su dopuštene računske operacije uz
uslov da joj je poznato poreklo odnosno odnos prema drugim nulama.
2. Postoji nula koja nema dimenziju – ona označava nepostojanje bilo čega.
3. Postoji negativna nula koja sabrana sa nulom iz tačke 1. daje nulu pod tačkom 2.
ako su te nule jednake. Nula iz tačke 2. dobija se oduzimanjem jednakih
vrednosti.
Ovo je možda skup gluposti, a možda i nije. Prilažem ilustraciju kojom pokušavam da objasnim ovo što sam rekao.
(Ovde ni na koji način nije pomenut ni jedan učesnik u raspravi jer to jednostavno nije potrebno).
[ uranium @ 29.09.2006. 18:14 ] @
@galet@world:
Verovatno nisam sve dobro shvatio, ali makar da se "pomerimo s nule" 
Neka je  univerzum nekih mat. objekata a  univerzum nekih njihovih elementarnih i nezavisnih svojstava i neka za svako neprazno 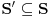 postoji objekat u  čiji se univerzum svojstava poklapa sa  .
Neki od pomenutih pojmova se uzimaju kao polazni. U opštem slučaju postoji i opasnost od pojave Raselovog paradoksa - ali za ovu priliku pretpostavićemo da su takve neprijatnosti otklonjene 
Nezavisnost treba shvatiti na sledeći način:
neka je 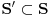 (stroga inkluzija) i neka je 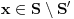 , onda postoji objekat u  koji ima sva svojstva iz 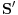 ali nema svojstvo  .
E sad, za svaki objekat 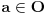 rećićemo da je nula u odnosu na neko 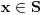 akko objekat  nema svojstvo  .
ovde nisam siguran da li sam dobro interpretirao tvoje viđenje, jer može biti da si ti želeo samo jednu nulu datog tipa - kolekcija ovih "mojih" nula u odnosu na isto svojstvo bi se (uz neke dodatne uslove) mogla smatrati tom jednom nulom
Na osnovu date definicije, za zadato svojstvo  može se desiti da postoji više različitih objekata koji su nula u odnosu na  .
Primeri:
a) 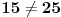 ali 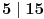 i 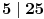 - ovde je svojstvo: "broj nije deljiv sa 5", pa su dati brojevi ipak jednaki u odnosu na to svojstvo (tj. nemaju ga).
b) Posmatrajmo skupove tačaka u ravni. Možemo da uočimo klasu svih onih čija je mera (tj. površina) jednaka nuli ili ne postoji. U tu klasu spadale bi recimo sve duži, kružne linije, najviše prebrojivi skupovi tačaka itd.
Zvanično se pravi razlika između skupova tačaka u ravni koji nemaju površinu (jer odgovarajući limes ne postoji) i skupova mere (površine) nula (gde limes postoji ali je jednak nuli) iako bi se i za ove poslednje moglo reći da nemaju površinu.
Dakle, one nule pod 1. shvatam kao objekte koji nemaju neko posmatrano svojstvo  , ali zato imaju neka druga svojstva.
Apsolutna nula bi trebalo da bude objekat koji nema ni jedno svojstvo, pa se može raspravljati da li takav objekat postoji ili je to samo sintaksna tvorevina.
Ako su  i  oznake za npr. isti ceo broj, onda skup 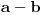 po svim zvaničnim definicijama postoji (i nije prazan).
Nasuprot tome, umesto da kažemo da nema razlike među skupovima  i  obično kažemo da je skup 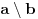 prazan (dakle, postoji ali je prazan).
I pored svega, priznajem da me kod 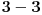 intuicija ipak vuče ka 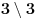  postojanje praznog skupa je uvedeno aksiomatski (tj. kao posledica nekih aksioma)
postojanje praznog skupa je uvedeno aksiomatski (tj. kao posledica nekih aksioma)
Dakle, nepostojanje se ponekad može prerušiti u odgovarajuće postojanje 
Što se tiče negativne nule, i sabiranja suprotnih nula - tu nisam siguran šta bi valjalo uraditi 
Može li neko dodatno pojašnjenje?
Za sad, i pored upornog traganja, nisam uspeo da pronađem primer gde bi se jasno videlo da neka mat. teorija ima "rupu" u smislu da radi sa objektima koji ne postoje...jedina mogućnost koju vidim je da se nekako ospori postojanje praznog skupa...
[ galet@world @ 30.09.2006. 11:01 ] @
@uranijum
Ja sam to ovako razumeo ( ispravi me ako grešim): Određen skup brojeva ili određena vrsta brojeva nema neka svojstva koja ima druga vrsta brojeva, iako obje vrste spadaju po nekim drugim svojstvima u neki «širi» skup.
Nepostojanje nekih svojstava čini mi se da izjednačavaš sa nulama za neku vrstu brojeva gde te nule znače nepostojanje («nevaženje»)tih svojstava za tu vrstu brojeva. Ako si to mislio – slažem se.
E sad – nepostojanje se, naravno, ne može u principu poistovetiti sa nevaženjem.
Ali u konkretnom slučaju čini mi se da može. Na primer da karikiram: brojevima ne možemo pripisati svojstvo brzine, temperature, elastičnosti i t. d. iako ti fenomeni za sebe postoje. Na jednak način nevaženje nekih svojstava za neki skup brojeva možemo poistovetiti sa nepostojanjem tih svojstava za taj skup. Ali za taj skup, a ne u principu.
Ako pogledamo četiri osnovne računske operacije, onda se operacija oduzimanja razlikuje od ostalih po tome što rezultat oduzimanja dva ista broja označava nepostojanje ako je oduzimanje potpuno.
Pod potpunim oduzimanjem smatram ukidanje nečeg ili otklanjanje nečeg bez ikakvih ostataka, za razliku od nepotpunog oduzimanja gde je rezultat nula, ali ima dimenziju. Konkretno u prilogu moje prethodne poruke prikazao sam duž kao takav ostatak t. j. kao površinu nulte vrednosti. Suma pet takvih površina opet ima vrednost nula [cm2], ali ta vrednost je ipak pet puta veća. To važi za svaki broj izuzev za beskonačno. Upravo ova činjenica svrstava nulu i beskonačno u čudesne fenomene. Sklon sam da tvrdim da i nula i beskonačno predstavljaju ustvari beskonačne skupove brojeva čija svojstva još nisu u potpunosti istražena.
U istraživanju tih svojstava pomaže nam jednakost odnosa između tih brojeva i konačnih brojeva.
Ovo za sledeću poruku, da sad ne bude preopširno.
[ uranium @ 30.09.2006. 13:16 ] @
@galet@world:
Mislim da si me razumeo, s tim da se nisam ograničio samo na brojeve.
U stvari, ja sam pokušao nekako da izvučem suštinu onog primera koji si naveo u prilogu prethodne poruke - naravno - ne tvrdim da sam u tome uspeo 
Citat: galet@world:
E sad – nepostojanje se, naravno, ne može u principu poistovetiti sa nevaženjem.
Ali u konkretnom slučaju čini mi se da može. Na primer da karikiram: brojevima ne možemo pripisati svojstvo brzine, temperature, elastičnosti i t. d. iako ti fenomeni za sebe postoje. Na jednak način nevaženje nekih svojstava za neki skup brojeva možemo poistovetiti sa nepostojanjem tih svojstava za taj skup. Ali za taj skup, a ne u principu.
Slažem se. Mada, imam utisak da je uvek moguće prevesti tvrdnju u kojoj se javlja pojam nevaženja u ekvivalentnu u kojoj figuriše samo pojam nepostojanja - naravno, pitanje je da li posmatrana teorija dopušta odgovarajuća jezička proširenja. E sad da li ovo poslednje (pod uslovom da je uopšte tačno  ) znači da su nepostojanje i nevaženje zapravo dva lica iste stvari? U ovom momentu bih rekao da jesu...
Citat: galet@world:
Ako pogledamo četiri osnovne računske operacije, onda se operacija oduzimanja razlikuje od ostalih po tome što rezultat oduzimanja dva ista broja označava nepostojanje ako je oduzimanje potpuno.
Pod potpunim oduzimanjem smatram ukidanje nečeg ili otklanjanje nečeg bez ikakvih ostataka, za razliku od nepotpunog oduzimanja gde je rezultat nula, ali ima dimenziju.
Intuitivno, ti si potpuno u pravu. Međutim, na osnovu zvaničnih definicija, razlika (misli se na op. oduzimanja, a ne na skupovnu razliku) dva ista cela broja je beskonačan skup. Evo primera:
Ceo broj  definišemo kao skup uređenih parova 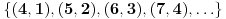 u poslednjem zapisu sve oznake za brojeve odnose se na prirodne brojeve
u poslednjem zapisu sve oznake za brojeve odnose se na prirodne brojeve
pa bi razlika 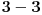 bila u stvari skup ur. parova 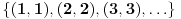 što je upravo skup kojim se definiše ceo broj  .
Ali, ako posmatramo skupovnu razliku između (skupa)  i (skupa)  (dakle, 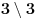 ) - tj. ako se pitamo koje to elemente skup  ima a skup  nema  - vidimo da je odgovor prazan skup tj. takvih elemenata nema.
Naravno, potpuno sam svestan da u praksi smisao (i upotreba) izraza 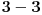 daleko više odgovara smislu (i upotrebi) izraza 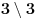 nego smislu definicije koju sam naveo 
Citat: galet@world:
Konkretno u prilogu moje prethodne poruke prikazao sam duž kao takav ostatak t. j. kao površinu nulte vrednosti. Suma pet takvih površina opet ima vrednost nula [cm2], ali ta vrednost je ipak pet puta veća. To važi za svaki broj izuzev za beskonačno. Upravo ova činjenica svrstava nulu i beskonačno u čudesne fenomene. Sklon sam da tvrdim da i nula i beskonačno predstavljaju ustvari beskonačne skupove brojeva čija svojstva još nisu u potpunosti istražena.
Ovde imamo jedan problem, jer koristeći se onom teoremom koja kaže da i duži različitih dužina imaju isti broj tačaka, mogli bismo da tvrdimo (ako želimo) da je suma pet onakvih površina u stvari i 555 puta veća od polazne. Dakle, za ovakva razmatranja mislim da su nam neophodne još neke dodatne definicije... iako se suštinski slažem sa zaključkom koji izvodiš (pogledaj kraj ove poruke). Štaviše, jedan od pokušaja definisanja one negativne nule i sabiranja suprotnih nula me je (ponovo) naveo na zaključak da je apsolutna nula u stvari beskonačna - suprotno polaznoj pretpostavci 
Dakle, ima tu nečeg  samo još uvek ne vidim pravi "okvir"...
[ galet@world @ 30.09.2006. 21:37 ] @
@uranijum
Rekao sam u prethodnoj poruci da nam opstajanje odnosa među konačnim i beskonačnim veličinama pomaže da otkrijemo neka svojstva beskonačnih veličina (izvinjavam se što se ja ne služim korektnom matematičkom terminologijom, ali se nadam da ćeš shvatiti šta sam hteo da kažem).
Citat: Ovde imamo jedan problem, jer koristeći se onom teoremom koja kaže da i duži različitih dužina imaju isti broj tačaka, mogli bismo da tvrdimo (ako želimo) da je suma pet onakvih površina u stvari i 555 puta veća od polazne. .
Ja, za sada, nikako ne uspevam da se pomirim sa tom teoremom, a evo pokazaću i šta mi tu smeta.
Održanje odnosa koje ću pokušati da pokažem upravo negira tu teoremu.
Evo prilogā:
[ Nedeljko @ 02.10.2006. 11:16 ] @
galet@world
O greškama ćemo otom-potom, kada lepo naučiš realne brojeve i pročitaš šta si pisao na datu temu.
[ galet@world @ 02.10.2006. 11:56 ] @
U konkretnom slučaju lično obraćanje u bilo kom vidu je nepoželjno.
Učenje realnih brojeva iz nekih udžbenika podrazumeva i usvajanje grešaka i nadgradnje nad tim greškama.
[ uranium @ 02.10.2006. 18:14 ] @
@galet@world:
Pogledajmo detaljnije prvu konstrukciju iz tvog priloga:
[att_img]
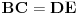 , 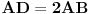 , 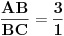 i 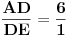
Umesto proporcionalnog smanjivanja, možemo samo reći da je jedinična duž unapred data i da je dužina 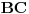 proizvoljna (ali ne nula).
Dakle, kada bismo u procesu proporcionalnog smanjivanja pogledali sliku ona bi bila ista kao i polazna, jedino bi se promenio odnos svih duži prema onoj unapred datoj jediničnoj duži.
E sad, šta se dešava kada 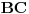 (a time i  ) postane 0?
Na osnovu postojećih definicija, više nemamo trougao 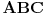 pa ne možemo ni govoriti o odnosu dužina kateta, jer tih kateta više nema...
S druge strane 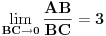 a npr. 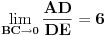 pa te možda to navodi na misao o očuvanju odnosa...
Ali, ako pogledamo definiciju limesa, videćemo da u navedenim primerima 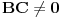 .
Dakle, limes niti "zna" šta se dešava u tački ka kojoj teži parametar, niti ga to "zanima" 
Drugim rečima, ako smo već došli u situaciju da su se tačke 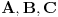 poklopile - više nemamo načina da rekonstruišemo način na koji su one dospele u tu poziciju...
Što se tiče onog razmatranja u vezi sa dužima različitih dužina i broja tačaka, složićeš se da na osnovu postojećih definicija krug i tačka nisu isto. Dalje, nije bilo nužno da se koriste dvodimenzionalni krugovi - mogli smo upotrebiti jednodimenzionalne krugove tj. intervale - tada bi bilo za nijansu jasnije da je ono zapravo priča o odnosu dužina dvaju duži i o tome šta se dešava kada nepodudarne duži merimo istom jedinicom mere a šta kada ih merimo različitim jedinicama.
I u tom slučaju, ako se držimo postojeće definicije limesa, informacija o odnosu dužina (a pogotovu o br. tačaka) se potpuno gubi u momentu kada se duži degenerišu u tačke.
Naravno, lako je tražiti mane nečemu što tek treba stvoriti, bilo bi daleko interesantnije ispitati da li je moguće napraviti zasebnu teoriju u kojoj bi nule pamtile poreklo...
Na kraju, vrlo je moguće da ja još uvek nisam ukapirao ideju o kojoj pričaš...
Možda bi sve to moglo da prođe u Nestandarnoj Analizi? Nažalost, to će morati neko drugi da ispita, jer ja dotičnu "Ana-Lizu" ne poznajem  Možda će nam Nedeljko preporučiti neku literaturu iz NA i propratne Logike?
Možda će nam Nedeljko preporučiti neku literaturu iz NA i propratne Logike?  [Ovu poruku je menjao uranium dana 02.10.2006. u 20:08 GMT+1]
[Ovu poruku je menjao uranium dana 02.10.2006. u 20:08 GMT+1]
[ galet@world @ 02.10.2006. 20:43 ] @
@uranijum
Meni se čini da smo mi na zajedničkom poslu istraživanja valjanosti nekih zaključaka koji nam se nameću i međusobno se isključuju, ili potvrđuju.
Ako pogledaš one preseke pravih koje sam nazvao slučaj I i slučaj II očigledno je da se razlikuju, ili da izbegnem reč "očigledno" prave se seku pod različitim uglovima i preseci su različiti. Zašto?
Zato što se tačke A, B i C nisu poklopile i imaju drukčiji razmeštaj u slučaju I u odnosu na razmeštaj u slučaju II, jer da nije tako preseci bi jednako izgledali.
A kako izgledaju - izgledaju upravo onako kako uslovljavaju ti zadržani odnosi.
Citat: I u tom slučaju, ako se držimo postojeće definicije limesa, informacija o odnosu dužina (a pogotovu o br. tačaka) se potpuno gubi u momentu kada se duži degenerišu u tačke.
Mislim da taj momenat nikada ne nastupa dok god postoje dužine ma koje veličine sa dimenzijom; u protivnom dužine ne postoje pa se ne može govoriti o svojstvima ničega.
Ma koliko delili neku dužinu izraženu u santimetrima ili bilo kojoj drugoj jedinici za dužine - ti delovi neće izgubiti svojstvo (t. j. dimenziju) dužine. Ne postoji beskonačnost koja će ukinuti to svojstvo i ne postoji momenat kada će tačka dobijena na ovaj način izgubiti to svojstvo. Tačka koja nema to svojstvo je nešto drugo - to je apsolutna nula kojoj je osnovno svojstvo da postoji u vidu nepostojanja.
Ponovo moram da kažem da je nula čudesan fenomen.
[ uranium @ 02.10.2006. 21:21 ] @
Citat: galet@world:
Ako pogledaš one preseke pravih koje sam nazvao slučaj I i slučaj II očigledno je da se razlikuju, ili da izbegnem reč "očigledno" prave se seku pod različitim uglovima i preseci su različiti. Zašto?
Zato što se tačke A, B i C nisu poklopile i imaju drukčiji razmeštaj u slučaju I u odnosu na razmeštaj u slučaju II, jer da nije tako preseci bi jednako izgledali.
A kako izgledaju - izgledaju upravo onako kako uslovljavaju ti zadržani odnosi.
Naravno, to sam primetio - upravo iz tog razloga sam i započeo priču o limesima a i na crtežu prikazao dva trougla sa različitim nagibima hipotenuze. Oni limesi upravo predstavljaju recipročnu vrednost izvoda f-ja koje odgovaraju pomenutim hipotenuzama tj. kotangense odgovarajućih uglova.
Poenta je u tome da ako krenemo da smanjujemo odgovarajuću katetu, a pri tom zadržimo proporcionalnost, u graničnom slučaju sva temena će se poklopiti, dakle sve tačke 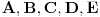 će se naći na istom mestu - i kako onda da jednoznačno kažeš gde je koja tačka bila pre toga? Naprosto, to nije moguće.
Citat: galet@world:
Mislim da taj momenat nikada ne nastupa dok god postoje dužine ma koje veličine sa dimenzijom; u protivnom dužine ne postoje pa se ne može govoriti o svojstvima ničega.
Slažem se, ali meni se učinilo da ti želiš da se oni krugovi degenerišu u tačke.
Citat: galet@world:
Ma koliko delili neku dužinu izraženu u santimetrima ili bilo kojoj drugoj jedinici za dužine - ti delovi neće izgubiti svojstvo (t. j. dimenziju) dužine. Ne postoji beskonačnost koja će ukinuti to svojstvo i ne postoji momenat kada će tačka dobijena na ovaj način izgubiti to svojstvo. Tačka koja nema to svojstvo je nešto drugo - to je apsolutna nula kojoj je osnovno svojstvo da postoji u vidu nepostojanja.
Opet se slažem, ali te delove ne zovemo tačkama. To se jednostavno zove interval - a interval nije tačka. [ galet@world @ 03.10.2006. 14:08 ] @
Citat: Poenta je u tome da ako krenemo da smanjujemo odgovarajuću katetu, a pri tom zadržimo proporcionalnost, u graničnom slučaju sva temena će se poklopiti, dakle sve tačke A, B, C, D, E će se naći na istom mestu - i kako onda da jednoznačno kažeš gde je koja tačka bila pre toga? Naprosto, to nije moguće.
Možda pod pojmom smanjivanje ne podrazumevamo isto značenje.
Smanjivanje je postupak koji ne može da se završi. Granični slučaj ne pripada pojavi koju promatramo. On ne može da se dobije smanjivanjem. On se dobija preskokom na novi kvalitet ili skokom na nepostojanje.
Na primer ako smanjujemo jednu stranu četvorougla - uvek će postojati četvorougao, ali ako prestanemo sa smanjivanjem i ukinemo tu stranu dobijamo nov kvalitet odnosno novu pojavu - trougao - koja ima druga svojstva.
Dakle, ukidanjem nekog elementa koji po definiciji pripada nekoj pojavi - skokovito prelazimo na drukčiju pojavu ili ukidamo pojavu t. j. skokovito prelazimo na pojavu nepostojanja ako je taj definicijski element bio jedini.
Ili jednostavnije: Ne možemo govoriti o očuvanju odnosa u trouglu, ako prelazimo na raspravu o nečem drugom.
Mislim da si se donjim citatom na neki način slažeš s ovim šta sam rekao
Citat: Opet se slažem, ali te delove ne zovemo tačkama. To se jednostavno zove interval – a interval nije tačka.
Smatram da je ovaj citat od izuzetne važnosti. On pomaže da dođemo do novih saznanja (da ne kažem otkrića!)
Interval je dobijen deobom neke duži na beskonačno mnogo delova - ta duž se opet može dobiti samo na jedan način: obrnutim postupkom t. j. množenjem tog intervala sa istom tom beskonačnošću iliti sabiranjem svih tih intervala. Dimenzija kao svojstvo postoji i kod duži i kod intervala.
Tačka nije interval (kao što kažeš), pa nema ni dimenziju – tačka prema tome nije dobijena beskonačnim deljenjem neke duži, pa se prema tome od tačaka ne može ni obrnutim postupkom dobiti duž!!! Jer odakle duži dimenzija ako bi bila sastavljena od elemenata koji nemaju dimenziju?
Tu ni beskonačnost ne pomaže – jer beskonačnost nije ključ s kojim se iz ničega stvara nešto.
U beskonačno mnogo trouglova nema ni jedan četvorougao, ma kolika bila ta beskonačnost. Trougao i četverougao su jednostavno dve različite pojave.
To isto važi za tačku i interval. To su jednostavno dve različite pojave. Tačka nema dimenziju, a interval ima.
Ovde dolazimo do odgovora na tvoje često postavljano pitanje koje se može i ovako “prevesti”: Šta ja ustvari hoću?
Ja hoću da definišem razliku između nule koja nema dimenziju i nule koja ima dimenziju.
Te dve nule nisu ravnopravne u odnosu na beskonačnost. Nulu bez dimenzije poistovetio bih sa tačkom, a nulu koja ima dimenziju sa beskonačno malim intervalom. Ovde bi trebalo definisati beskonačno mali interval. Možda bi moglo ovako: Beskonačno mali interval je nula koja ima dimenziju. Množenjem tog intervala bilo kojim konačnim brojevima dobijaju se opet nule koje su proporcionalne tim brojevima i međusobno su uporedive. Množenjem tog intervala beskonačnim brojevima dobijaju se konačne vrednosti dužina koje su proporcionalne tim beskonačnim brojevima.
Beskonačnost nije ključ koji menja svojstvo tačaka t. j. njihovu bezdimenzionalnost i ne pretvara ih u interval koji ima dimenziju.
Ako tačka nema dimenziju, onda ni beskonačno mnogo tačaka nema dimenziju. Sad dolazimo do “katastrofalnog otkrića”:
Prava nije skup tačaka nego skup intervala.
Govoriti o “količini” ili o “istom broju” tačaka u bilo kom smislu a pogotovu kao sadržini nekih različitih dužina je jednostano besmisleno.
Jednostavno zato što bezdimenzionalne tačke nisu gradivni elementi dužina.
Što se tiče ovih naših razmišljanja nekako mi se čini da nam tu neće pomoći ni neka tuđa Ana ni Liza, prepušteni smo sami sebi pa dokle dotle.
Preopširan sam, znam, ali izvini malo sam se zaneo pa sam prikazao tok mog neveštog razmišljanja, a ne neki sažet rezultat.
[ uranium @ 03.10.2006. 17:46 ] @
@galet@world:
Onaj deo o skokovitim prelazima si odlično napisao - upravo je to bila suština moje zamerke.
U onom dokumentu razmatraš i situaciju u kojoj su one paralelne prave postavljene na (kako kažeš) isto mesto, odatle odmah sledi da su tačke  i  jedno te isto a zbog toga i tačke  i  . Odmah nakon toga izvodiš neke zaključke o odnosu nekih "duži".
Dakle, moja primedba se odnosila na ono što si u tom trenutku mislio/napisao - sada mi se čini da si delom promenio mišljenje (što nema nikakvu negativnu konotaciju).
Znači ne prihvataš da su se tačke  i  poklopile?
Ako je odgovor potvrdan, onda nemamo prava da dužinu 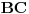 nazivamo nulom.
Ako pričamo o intervalima, moram da priznam da sam u brzini umesto reči "duž" upotrebio reč "interval" jer u standardnoj interpretaciji strukture realnih brojeva intervalima odgovaraju duži (i obratno). Pribojavao sam se da će doći do nesporazuma a eto izgleda da se to i desilo.
Dakle, ako ti nije teško opiši na šta si mislio kada si napisao:
Citat: galet@world:
Interval je dobijen deobom neke duži na beskonačno mnogo delova
U slučaju da se ispostavi da si pod intervalom podrazumevao nešto što ne odgovara definiciji intervala, zamolio bih te da upotrebljavamo neki drugi izraz, recimo "beskonačno mali interval" ili šta već bude prikladno.
Da pomenem i to da beskonačno mali interval ne može da se definiše a da ostanu na snazi sve aksiome kojima uvodimo strukturu realnih brojeva. Dakle, jedina šansa je da se napravi potpuno odvojena teorija.
Kada i upotrebim (istina neprecizan) izraz "broj tačaka" uvek mislim na kardinalni broj odgovarajućeg skupa - a taj pojam ima vrlo preciznu definiciju... 
Što se tiče odnosa između tačaka i intervala (u izvornom smislu), to je izuzetno zanimljiva tema i zaista mi je drago da smo došli do toga.
Postavio si nekoliko vrlo uzbudljivih pitanja, ali ja neću biti u stanju da pišem o tome bez upotrebe nekih tehnika, a bojim se da u tom slučaju nećeš imati volje da to pratiš. Pogledaj nešto o neprebrojivosti Kantorovog skupa. Grubo govoreći, konstrukcija Kantorovog skupa može se shvatiti kao dekompozicija datog intervala (tj. duži) u totalno nepovezan skup, dakle u skup rastavljenih tačaka (taj dobijeni skup biće iste kardinalnosti kao i polazni interval).
Na kraju, ne vidim zašto bismo unapred potcenjivali iskustva i drugih ljudi - tim pre ako idu u prilog našim stavovima.
Ne želim da odvučem raspravu u sociološke vode, ali reći ću samo to da bih bio vrlo iznenađen kad bi se ustanovilo  da je neki od članova skupa {Mogli, Tarzan, Romul & Rem,...} samostalno došao do pojma beskonačno malog 
Što se mene tiče, budi opširan koliko god je potrebno  [Ovu poruku je menjao uranium dana 03.10.2006. u 19:25 GMT+1]
[Ovu poruku je menjao uranium dana 03.10.2006. u 19:25 GMT+1]
[ uranium @ 04.10.2006. 11:26 ] @
galet@world:
Citat: galet@world:
Govoriti o “količini” ili o “istom broju” tačaka u bilo kom smislu a pogotovu kao sadržini nekih različitih dužina je jednostano besmisleno.
Jednostavno zato što bezdimenzionalne tačke nisu gradivni elementi dužina.
Da pokušam da kažem otvorenije ono što sam već rekao prethodnom porukom.
Kada iz intervala, Kantorovim postupkom, odstranimo odgovarajuće podintervale, na kraju ostane dovoljno tačaka da se od njih može konstruisati interval bilo koje dužine - ako želimo, čak i interval 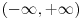 . Zapravo, možemo i više... Od tih istih tačaka možemo da napravimo i celu ravan, ili ceo prostor, ili... 
[ galet@world @ 04.10.2006. 15:45 ] @
@uranijum
Prave a i b sam stavio na isto mesto da bih izbegao oduzimanje inače ne bi bilo ni jedne prave pa ni površine. Ako postoji prava onda postoji i njena dimenzija u smislu “širine” prave. Rekao sam da vertikalna kateta postoji t. j. da ima vrednost 0 cm, a to je ta širina. Na krajevima takve katete koja ima dimenziju (zato što postoji prava) možemo da zamislimo bezdimenzionalne tačke B i C koje nisu na istom mestu.
Ranije sam pokazao da duž ima površinu 0 cm2, a to je moguće samo u slučaju ako duž ima dve dimenzije. Prava koja nema dve dimenzije ne postoji.
Sve je ovo i čudno i interesantno.
Na primer: prava ima i gornju i donju stranu i prednju i zadnju i t. d. ali verujem da malo ko misli o tom.
Postoji li prava koja nema ove atribute?
Kad je u pitanju interval (da ne citiram) ja sam rekao ono što mi se učinilo da ti podrazumevaš pod tim izrazom. Ako nisam pogodio, onda bi bilo najbolje da ti kažeš pravu (zvaničnu) definiciju intervala.
Ja imam žarku i želju i volju da se popnem na Mesec, ali nažalost, nemam tolike merdevine – tako će izgleda biti i sa Kantorovim fraktalom i kardinalnim brojem, ukoliko ti ne budeš imao volje da te i slične stvari kažeš malo pravoslavnijim jezikom, koji ja donekle razumem (uostalom valjda i sam vidiš s kim imaš posla!!!).
U zadnjoj poruci govoriš o dovoljno tačaka koje mogu da ispune ceo prostor, ali ja ne znam šta ti misliš kakve su te tačke t. j. da li imaju dimenziju zapremine ili nemaju nikakvu dimenziju.
[ uranium @ 07.10.2006. 15:35 ] @
@galet@world:
Umalo da mi padne zastavica 
Gde smo ono stali? Ah da...sad si krenuo i protiv nekih teorema klasične geometrije i topologije ali dobro... 
Meni se ipak čini da ni ti ne veruješ u to što pišeš, jer što bi se plašio oduzimanja kad (kako kažeš) one dve tačke uopšte ne stoje na istom mestu? One bi u tom slučaju sasvim lepo "preživele" oduzimanje.
Rečenice u kojima si upotrebljavao pojam dimenzije, nisu u skladu sa topološkom definicijom dimenzije.
Prava u ravni deli tu ravan na dve klase (tj. na dve otvorene poluravni) ali u svakoj okolini proizvoljne tačke te prave nalaze se tačke iz obe poluravni, dakle to što ti zoveš "gornjom" i "donjom" stranom prave zapravo je jedna jedina "strana". Sličnan komentar važi i za "prednju" i "zadnju" stranu.
Kada se kaže interval, obično se misli na odgovarajući podskup nekog uređenog skupa. U konkretnom primeru ja sam imao u vidu zatvorene intervale realnih brojeva tj. skupove oblika 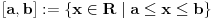 . U standardnoj geom. interpretaciji strukture realnih brojeva - pravi zatvoren interval (tj. takav da 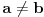 ) je isto što i odgovarajuća zatvorena duž tj. skup svih tačaka između krajnjih tačaka koje su pridružene brojevima  i  (uključujući i te krajnje tačke).
Onaj nesporazum je verovatno posledica mog nepreciznog izražavanja, jer kada sam rekao interval, mislio sam na rezultat dobijen posle bilo kog (ali konačnog) broja deljenja, a ti si verovatno mislio na rezultat dobijen beskonačnim deljenjem...
Što se tiče intenziteta želje i nepoznavanja jezika - nisi me ubedio ni u jedno  a nadam se da to neću morati dodatno da obrazlažem  . I pored toga, voljan sam da pomognem (u razumnim granicama) - dakle, postavi konkretno pitanje pa ću se potruditi da razjasnim šta bude potrebno.
Ako pričamo o topološkoj dimenziji, skup koji sadrži samo jednu tačku ima dimenziju nula.
Da ponovim već  -ti put  - tvrdnje koje si izneo mogu se osporiti unutar nekih postojećih mat. teorija (pod uslovom da se prvo usklade definicije  ). Da li već postoji ili se može napraviti neka mat. teorija koja je saglasna sa tvojim idejama - ja to u ovom momentu ne znam...
[ galet@world @ 08.10.2006. 11:41 ] @
@uranijum
Ja o ovim stvarima razmišljam isključivo zato što mi se čine interesantnim i što neke od tih stvari ne mogu (bar za sada) da prihvatim.
One dve “preživele” tačke nisu ni živele, mislio sam ustvari na krajeve dimenzionalne tačke koja ima dimenziju 0 cm.
Ipak bih želeo da kažeš šta misliš o površini duži.
Duž nije broj, površina nije broj, sila nije broj, ugao nije broj i t. d. pa se pomoću brojeva te pojave ne mogu ni objasniti. Bilo koju od tih pojava možemo samo porediti sa istom takvom t. j. tom pojavom. U tom cilju dogovorilii smo se o nekim veličinama tih pojava kao jediničnim. Jedinica neke pojave mora imati isti kvalitet kao ta pojava.
Stoga mi se čini pogrešnim smatrati duž skupom bezdimenzionalnih tačaka, jer takve tačke nemaju kvalitet dimenzije. Tu ne pomaže ni beskonačnost, jer se taj kvalitet ne može nikako stvoriti ni iz čega.
Ako neku duž podelimo na beskonačno mnogo delova dobićemo nulu koja ima dužinu. Taj kvalitet se tom deobom ne uništava. Samo takve nule mogu biti gradivni elementi duži. Bezdimenzionalnih tačaka možeš na dimenzionalnu tačku staviti koliko god hoćeš, jednostavno zato što za njihov smeštaj nije potreban nikakav prostor, površina ili dužina.
Kod duži krajnja bezdimenzionalna tačka znači prestanak kvaliteta i ona prema tome ne pripada toj duži.
Duž i bezdimenzionalna tačka su suštinski dve različite pojave i ne mogu se transformisati jedna u drugu.
Rekao si da ti ne smeta opširnost, ali to se verovatno ne odnosi na lupetanje, pa za svaki slučaj da skratim.
[ uranium @ 08.10.2006. 14:34 ] @
@galet@world:
Sva pitanja koja si pokrenuo su izuzetno zanimljiva i smatram da je uvek korisno postavljati slična pitanja.
Međutim, čini mi se da se naša shvatanja matematike značajno razlikuju. Izgleda da ti misliš da postoji neka "matematička realnost" - da neke stvari naprosto "jesu" a neke "nisu". Takvo viđenje je odavno napušteno...
Citat: galet@world:
One dve “preživele” tačke nisu ni živele, mislio sam ustvari na krajeve dimenzionalne tačke koja ima dimenziju 0 cm.
Ipak bih želeo da kažeš šta misliš o površini duži.
Ne znam kako možemo da pričamo o "krajevima" tačke kad tačka nema delove...
naravno, pod uslovom da mislimo na ono što se zove tačkom u klasičnoj geometriji
Prema postojećim definicijama površine - duž ima površinu 0.
Citat: galet@world:
Duž nije broj, površina nije broj, sila nije broj, ugao nije broj i t. d. pa se pomoću brojeva te pojave ne mogu ni objasniti.
Kad bi te sad čuli pitagorejci...završio bi kao Hipas 
Citat: galet@world:
Bilo koju od tih pojava možemo samo porediti sa istom takvom t. j. tom pojavom. U tom cilju dogovorilii smo se o nekim veličinama tih pojava kao jediničnim. Jedinica neke pojave mora imati isti kvalitet kao ta pojava.
To ne mogu da prihvatim. Evo ti jedan primer. Uočimo prirodan broj 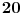 , on ima razne kvalitete  ali recimo da me ovom prilikom zanima to što je on deljiv sa 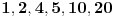 .




A koji od tih kvaliteta možemo pripisati jedinici? 
Citat: galet@world:
Stoga mi se čini pogrešnim smatrati duž skupom bezdimenzionalnih tačaka, jer takve tačke nemaju kvalitet dimenzije. Tu ne pomaže ni beskonačnost, jer se taj kvalitet ne može nikako stvoriti ni iz čega.
Razmotri još jednom Kantorov skup...
Ja mislim da smo sasvim dovoljno proučili ove ideje sa stanovišta nekih postojećih mat. teorja.
Ako se slažeš sa prethodnim, možda bi mogao da zapišeš na jednom mestu sve te ideje u vidu spiska aksioma, i njihovih prvih posledica, pa da vidimo možemo li reći nešto o njihovoj neprotivrečnosti.
[Ovu poruku je menjao uranium dana 08.10.2006. u 17:08 GMT+1]
[ galet@world @ 08.10.2006. 21:04 ] @
uranijum
Citat: Ne znam kako možemo da pričamo o "krajevima" tačke kad tačka nema delove...
Ja mislim na onakvu vrstu tačaka od kojih se može dobiti duž. Takve tačke imaju delove.
Citat: Prema postojećim definicijama površine - duž ima površinu 0.
To znam, ali (nemoj da se ljutiš!) pitao sam šta ti misliš o tome.
(Zaista ne znam šta je bilo sa Hipasom, a interesuje me!)
Citat: To ne mogu da prihvatim. Evo ti jedan primer. Uočimo prirodan broj 20, on ima razne kvalitete ali recimo da me ovom prilikom zanima to što je on deljiv sa 1,2,4,5,10,20.
Ovde sam verovatno pogrešio u terminologiji. Ti poistovećuješ kvalitet sa svojstvima – verovatno tako i treba, ali ja nisam to mislio. Mislio sam na onaj kvalitet koji razdvaja različite pojave, a ne na kvalitet iliti svojstva unutar iste pojave.
Zajednički kvalitet i jedinice i dvadesetice je da sadrže jedinicu. Silu ne možemo izraziti u sekundama nego samo nekom drugom silom. Svaka pojava se može izraziti samo nekim svojim delom, a ne nekom drugom pojavom.
To isto važi i za duž.
Svaka duž se može izraziti samo sa svojim delom, a taj deo ma koliki da je ima dužinu kao svojstvo kao i duž. Ako taj deo nema to svojstvo onda takvi delovi ne mogu stvoriti pojavu koja ima to svojstvo.
Naravno da svojstva neke pojave zavise od intenziteta te pojave, ali intenzitet podrazumeva različitu količinu jednakih delova te pojave.
Citat: Razmotri još jednom Kantorov skup...
Pretpostavljam da misliš da odavde sledi da se od bezdimenzionalnih tačaka može dobiti duž.
Ovo je zaista interesantna stvar – što više intervala oduzimaš to ih dvaput više ostaje. Ali ipak uvek ostaju intervali – a oni imaju dimenziju, odnosno nikad ne može nastati momenat kad intervali gube dimenziju i transformišu se u novu odnosno drukčiju pojavu. Na ovaj način se ne može isprazniti skup preostalih intervala, ali ni skup oduzetih intervala nikad nije 1. Ovo je postupak koji nema kraja i pomalo liči na Ahila i kornjaču.
Što se tiče tvog predloga - možda bi zaista trebalo srediti nekako te moje tvrdnje i napraviti nešto novo ili ih razbucati da im ni traga ne ostane ako su kontradiktorne. Trebalo bi razmisliti.
[Ovu poruku je menjao galet@world dana 08.10.2006. u 22:16 GMT+1]
[ Nedeljko @ 08.10.2006. 22:06 ] @
Poštovani uranijume,
Mislim da se džabe mučiš. Ovako mu ništa ne možeš objasniti. Izgleda da on kada me kritikuje da nekritički usvajam greške iz literature, zapravo i ne razume šta je to zapravo greška u matematici. Pogrešno zasnivanje nekog pojma je isključivo ono koje se ne može eliminisati iz formulacija iskaza (kao što su na primer teoreme), ili proizvodi nove zaključke na jeziku prethodno uvedenih pojmova. Pritom se tačno zna kako se dokazuje korektnost neke definicije (to jest, šta je matematička formulacija prethodno navedenih zakona konzervacije).
Međutim, čak i ako je definicija korektna, može se desiti da nema realizaciju, jer su navedeni uslovi protivrečni (što je ne čini nekorektnom). U tom slučaju, rasprava o tom pojmu može biti i formalno potpuno korektna (ako se ne tvrdi (osim hipotetički) da postoji realizacija te definicije), ali neće imati previše smisla. Da se ne bi previše natezali, treba da uči sledećim redom:
- Osnovno o skupovima
- Uređen par
- Relacije
- Preslikavanja
- Kardinalni brojevi
- Prirodni brojevi
- Celi brojevi
- Racionalni brojevi
- Košijevi nizovi u uređenom polju (na primer racionalnih brojeva)
- Realni brojevi
- Limesi
- Mera (na primer Žordanova)
U protivnom ćete se natezati oko "duži podeljene na beskonačno mnogo delova koji imaju dimenziju nula", "beskonačnom broju tačaka bez dimenzije koje ne mogu činiti duž, jer ona ima meru" i sličnih stvari. Tu kraja nema.
Sa druge strane, ti mu ne možeš napisati udžbenik analize, pogotovu besplatno na ES. Bolje mu preporuči literaturu, reci mu kojim redosledom, šta i odakle da čita, pa neka pita kada mu negde zapne. Ovako ne vredi, veruj mi.
[ galet@world @ 09.10.2006. 06:19 ] @
Radi se o tome da ja ne učim - ni sebe ni druge. Ja pitam i mislim da je ova rečenica iskrena, a ne kurtoazna:
"Sva pitanja koja si pokrenuo su izuzetno zanimljiva i smatram da je uvek korisno postavljati slična pitanja."
Nisam u potpunosti isključio učenje, ali ono ne treba biti slepo usvajanje tuđih zaključaka. Moja pitanja upravo i izražavaju sumnju u te zaključke, jer mi se čini da bi moglo i drukčije. Ne tvrdim da sam u pravu i biću zahvalan onom ko konkretno dokaže protivrečnost mojim tvrdnjama što je uranijum i predložio. Mislim da bi tako trebalo, a ne pričati uopštene i poznate principijelne stvari a neprimenjivati ih konkretno.
[Ovu poruku je menjao galet@world dana 09.10.2006. u 10:14 GMT+1]
[ galet@world @ 09.10.2006. 07:49 ] @
Za Nedeljka
Izračunaj:
1 – 1 = ?
1
-- = ?
∞
Uputstvo: reč «izračunaj» znači da treba umesto upitnika staviti rezultat bez bilo kakvih komentara.
[ djoka_l @ 09.10.2006. 12:54 ] @
galet: ugao jeste broj (za razliku od dužine, površine itd.)
Ugao se definiše kao odnos dužine luka i poluprečnika kruga - pa je tako pun krug 2pi (znači neimenovan broj). Da bi bilo zgodnije, ponekad se piše 2pi rad (odnosno radijan) ali radijan je uveden konvencije radi. Ugao je neimenovani broj jer predstavlja m/m (metar kroz metar). Stepen je samo način da se 2pi zapiše kao 360.
P.S. kada sam rekao da je dužina imenovana veličina, mislio sam na fiziku, a ne na matematiku. U matematici ne mora to da bude, to je "osobina" metričkog prostora i ne mora da ima nikakve vrednosti sa veličinom koja se meri metrom...
[ uranium @ 09.10.2006. 19:40 ] @
@djoka_l:
Pobrkao si meru ugla sa uglom.
Druga je stvar to što je u mnogim problemima dovoljno znati meru ugla...
@galet@world:
Mislim da je Nedeljkova poruka bila sasvim dobronamerna, a skrenuo nam je pažnju i na neke nepobitne činjenice.
Kao što to obično i biva u raspravama koje vuku ka filozofiji, posle nekog vremena se ispostavi da sagovornici imaju neki jezički nesporazum ili jednostavno ne umeju da saopšte "sadržaj" nekog pojma drugoj strani. To se nama desilo i na primeru "kvaliteta pojave"...
ja i dalje verujem da ona tvoja tvrdnja može da se ospori 
Matematika uglavnom ne boluje od te boljke - u tom smislu zaista bi pomoglo kada bi obojica koristili isti matematički jezik i "pojmovnik". 
Mislim da za sad ne vidiš "veliku sliku" Matematike a pre svega ulogu Logike u zasnivanju pojedinačnih mat. teorija, pa otuda valjda i neshvatanje konteksta "primedbi" koje si izneo kao i novih ideja koje si dao. Da pokušam da budem malo precizniji, pogledaj primera radi aksiome Tarskog za ravansku euklidsku geometriju - posebno obrati pažnju na spisak dokazanih osobina tog sistema (konzistentnost pre svega).
kad si već tamo, pogledaj i Identity of betweenness 
Još jedan koristan link: logički status euklidske geometrije.
Da pitam još jednom šta misliš o sledećem:
• Da li duž ima jednu jedinu prirodu koju (tek?) treba otkriti?
Citat: galet@world: Za Nedeljka
Izračunaj:
1 – 1 = ?
1
-- = ?
∞
Uputstvo: reč «izračunaj» znači da treba umesto upitnika staviti rezultat bez bilo kakvih komentara.
Prvo pitanje ima sasvim jasan i nedvosmislen odgovor u zavisnosti od strukture u kojoj ga posmatraš.
Ja sam bio ubeđen da smo sa time završili jer nisi izneo ni jednu primedbu kad sam pisao o tome.
Što se tiče drugog pitanja u mat. analizi se često radi sa tzv. proširenom strukturom realnih brojeva. Oznaka  se koristi isključivo da bi se olakšalo izražavanje. Kada se pomenuto proširenje uvodi, vrlo precizno se iznese odnos novouvedenih elemenata  i 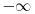 prema postojećim operacijama i relacijama (uglavnom rel. poretka) na strukturi. Sve što matematička analiza "ima da kaže", može se iskazati i bez upotrebe tih simbola.
Shvatam da ti pokušavaš da istakneš razliku između rezultata prvog i drugog izraza (zbog načina na koji su dobijeni), ali nažalost izgleda da je Nedeljko u pravu - trebalo bi da pogledaš kako se uvode pomenuti simboli i naravno da vidiš šta je po definiciji 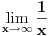 . Dakle, nadam se da se ne ljutiš, ali zaista mi se čini da ti je pojam limesa nejasan. Limes možemo shvatiti kao svojevrsnu relaciju (zapravo operaciju) koja povezuje četiri stvari:
• funkciju (u našem slučaju 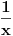 )
• argument f-je (u našem slučaju  )
• "tačku" ka kojoj "teži" argument (u našem slučaju  )
• broj ka kome vrednost f-je teži kad argument teži ka datoj tački (u našem slučaju broj  )
Dakle, ako napišemo 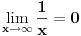 to samo znači da je  taj broj  za koji važi sledeće:
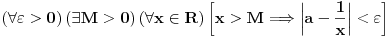
Ako nije jasno šta prethodna formula pokušava da kaže  reci pa ću pojasniti.
Dakle, 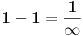
Citat: galet@world:
(Zaista ne znam šta je bilo sa Hipasom, a interesuje me!)
Citat: uranium:
Kad bi te sad čuli pitagorejci...završio bi kao Hipas 
Možda je potrebno da klikneš na reč "Hipas"? 
Citat: galet@world:
Ovo je postupak koji nema kraja i pomalo liči na Ahila i kornjaču.
Ahil i kornjača postoje i u tvom postupku deljenja duži (ili generisanja duži uz pomoć tzv. tačke sa dimenzijom) - pa smo na istom  [Ovu poruku je menjao uranium dana 09.10.2006. u 21:08 GMT+1]
[Ovu poruku je menjao uranium dana 09.10.2006. u 21:08 GMT+1]
[ galet@world @ 10.10.2006. 18:27 ] @
O Nedeljkovim dobrim namerama najbolje govori on sam:
Citat: Sa druge strane, ti mu ne možeš napisati udžbenik analize, pogotovu besplatno na ES.
Za razliku od tebe, kao što vidiš, on je odmah «pročitao» moje namere, a ti nikako da shvatiš šta ja ustvari hoću!
Citat: Da li duž ima jednu jedinu prirodu koju (tek?) treba otkriti?
Kao za tačku i za duž kažem da postoji duž koja ima površinu i dve dimenzije i duž koja nema površinu i ima jednu dimenziju.
Za pojavnu razliku od tačke duž ima dužinu kao svojstvo. Ta dužina je kontinuitet koji je posebna datost i koji se ne može objasniti ničim drugim jer sve drugo je drukčije – ništa osim kontinuiteta nije kontinuitet. Uzaludni su pokušaji objašnjavanja kontinuiteta tačkom, a možda i čudni jer i tačka je zagonetna tvorevina ljudskog uma i kao takva takođe posebna datost bez dimenzije.
Tačka kao mesto u prostoru i duž kao razmak između mestā nisu gradivni elementi ničega drugoga – oni su entiteti ili identiteti (ne znam pravi izraz) sami za sebe, a nema ni potrebe objašnjavati jedno s drugim.
Duž možemo deliti na manje delove, ali svaki taj deo ma koliko mali bio je kontinuitet a ne tačka ili skup tačaka. To bih nazvao očuvanjem osnovnog svojstva.
Ako silu podelimo na beskonačno mnogo delova svaki taj deo mora biti sila – ali ako ti delovi izgube svoje osnovno svojstvo onda se obrnutim postupkom više nikako ne može dobiti sila. Čime objašnjavamo silu? Ako kažemo da je to svojstvo materije – ništa nismo objasnili, a ne možemo objasniti silu ni njenim manifestacijama. To jednostavno ne treba ni činiti. To je pojava koja je takva, koja postoji i gotovo. Ako prihvatamo pojam sile zdravo za gotovo, zašto za pojam kontinuiteta izmišljamo neki drugi princip?
A sad da pokušamo na drugi način.
Kako se generiše duž od bezdimenzionalnih tačaka – ili je ovo možda zabranjeno pitanje?
Koliko duž sadrži tačaka – ili je ovo besmisleno pitanje?
Da li je beskonačno broj ili su to različiti brojevi t. j. da li su beskonačnosti međusobno različite i mogu li se međusobno porediti i da rezultat tog poređenja bude bilo koji realan broj?
Citat: Dakle, nadam se da se ne ljutiš, ali zaista mi se čini da ti je pojam limesa nejasan.
Ne ljutim se, a i šta bi vredelo. Glupost je Božji dar protiv koga se ništa ne može.
Limes sam shvatio kao granicu gde se gotovo svi članovi nekog skupa nalaze u proizvoljno malom intervalu u blizini granične vrednosti, a oni koji nisu tu su zanemarljiva sitnica u pogledu broja članova. Taj interval može biti proizvoljno mali pa opet isto i t. d.
Ali ne znam šta će mi limes i šta će mi prikaz smanjivanja intervalā neke funkcije prema nekoj nedostižnoj granici, osim da bih video da se u proizvoljno mali interval može smestiti beskonačan broj mestā koja odgovaraju članovima skupa.
Na bezbroj načina se duž može podeliti na svoje intervale, zašto je odabran ovaj način kad ni jedan tako dobijen interval nije jednak drugom.
Nekako mi se čini da limes ovde ništa ne objašnjava,on je samo broj kome se približavaju članovi skupa, pa mi se čini da bi možda bolje bilo pisati:
1
-- = 1 – 1 s tim što «1 – 1» nije rezultat te deobe nego označava granicu.
∞
Ako nije moguće jednostavno odnosno dovoljno razumljivo odgovoriti na moja pitanja jezikom kojim se ja služim, onda je sasvim opravdano uputiti me na literaturu i neki pedagoški redosled upoznavanja sa ovom problematikom. Ja, međutim, ne nameravam da postupim po ovom predlogu, ali to je, naravno, moj problem. Mislio sam da je moguće i direktno dobiti odgovore na neka pitanja, ali prevario sam se pa prema tome moram da odustanem. Hvala na razumevanju i strpljenju.
[ Farenhajt @ 10.10.2006. 23:14 ] @
Da se malo umešam, kad se već lome razna koplja.
Koliko se meni čini, galet@world govori o ovome:
1. Zamislimo skup geometrijskih tačaka u formi pravougaonika čija je dužina proizvoljna ali konačna, a širina mu iznosi tačno jednu tačku. Taj skup definišemo kao duž.
2. Zamislimo skup geometrijskih tačaka u formi pravougaonika čija je dužina proizvoljna ali konačna, a širina mu iznosi tačno dve tačke. Taj skup definišemo kao žešće zeznut skup.
Prema važećim teorijama o skupu realnih brojeva, žešće zeznut skup ne može postojati, ne može se čak svesti ni na duž, iako "strahovito liči" na duž, jer je skup realnih brojeva svuda gust, pa se ne mogu odabrati dve "susedne" tačke, pošto će između njih uvek postojati neprebrojivo mnogo tačaka.
Na osnovu toga, uopšte nije daleko od pameti njegova dilema da je "prirodna nula" suštinski različita od "realne nule", jer se prva dobija u jednom konačnom koraku, oduzimanjem jedan od jedan, nakon čega ne ostaje ništa, dok se druga zapravo i ne može dobiti mimo limesa, tj. beskrajnog procesa "istanjivanja" koji se nikad ne može završiti, ali čiju graničnu vrednost definišemo kao "realnu" nulu jer nam taj pojam treba za "dobru i lepu" teoriju realnih brojeva. Takođe, težnja ka što višem "faktoru dobrote" te teorije navodi nas da izjednačimo "prirodnu" i "realnu" nulu, jer se naprosto onda sve pojednostavljuje i daleko "lepše" uklapa nego ako bismo vozali dve različite nule.
[ uranium @ 10.10.2006. 23:38 ] @
@Farenhajt:
Ako prihvataš aksiomu izbora, taj žešće zeznut skup i te kako postoji 
Dakle, postoji dobro uređenje realnih pa time i susedni elementi u smislu takvog uređenja 
[ Farenhajt @ 11.10.2006. 00:05 ] @
Više sam pokušao da izvučem "zdravorazumski" ekstrakt iz postova galet@world-a nego što sam ulazio u to šta kad može, a kad ne može 
Tačke susedne po dobrom uređenju skupa realnih brojeva neće, koliko vidim, biti i "vizuelno" (geometrijski) susedne (tj. susedne na način koji bi bio srodan "susednosti" u skupu prirodnih brojeva)... Ili možda grešim?... A čitava dilema i proističe iz "vizuelnog" tumačenja "realne" nule. [ uranium @ 11.10.2006. 01:20 ] @
@Farenhajt:
Niko ne zna kako bi to dobro uređenje izgledalo, jedino se zna da ono postoji (pod datim pretpostavkama) - ja sam to naveo jednim delom kao zanimljivost a drugim delom kao ilustraciju nečeg o čemu pokušavam da pričam već poslednjih  postova 
Na primer euklidska geometrija ima razne modele a većina njih ne izgleda ni malo intuitivno - dakle pojam duži, linije...opisan nekim od standardnih sistema aksioma (i propratnim definicijama) uopšte ne mora da odgovara predstavi koju većina nas ima kada nam se pomene neki od tih pojmova.
Po pravilu, ključne stvari se ne dokazuju već se uzimaju kao aksiome, a u slučaju geometrije imamo dokazane mnoge lepe osobine odgovarajućeg sistema aksioma. Svako je slobodan da taj sistem preuredi po svom nahođenju ili izgradi potpuno novi i time (eventualno) dobije novu teoriju. Dakle, jedan od razloga zbog koga se ova rasprava toliko rasplinula je u tome što rečenice "Tačka ima delova" i "Tačka nema delova" same za sebe nemaju nikakvog matematičkog smisla. Matematički objekti nisu geografski objekti (ko je rek'o Slaviša B. Prešić?  ) pa da možemo da kažemo nešto tipa: "Beograd se nalazi na ušću Save u Dunav".
Klasičan primer šta znači matematička naspram laičke interpretacije mat. pojmova je recimo geometrijska predstava jedinične sfere u zavisnosti od nametnute metrike. Odgovarajuće slike mogu se videti ovde a čik probaj nekog neupućenog da ubediš da su sve ono slike i dvodimenzionih sfera (tj. kružnih linija)  [Ovu poruku je menjao uranium dana 11.10.2006. u 03:02 GMT+1]
[Ovu poruku je menjao uranium dana 11.10.2006. u 03:02 GMT+1]
[ Farenhajt @ 11.10.2006. 09:52 ] @
Sve je to u redu, ali opet - držim da je galet@world pošao od klasičnog, intuitivnog modela euklidske geometrije i došao do svega što je došao. I kao što si sam rekao, svako od nas može da sastavi sopstvenu aksiomatiku i da se njome silno ponosi. (Kao ilustraciju, uzmi naše dve aksiome u vezi s adicionim formulama  ) [ Nedeljko @ 13.10.2006. 20:23 ] @
Citat: galet@world: O Nedeljkovim dobrim namerama najbolje govori on sam: Citat: Sa druge strane, ti mu ne možeš napisati udžbenik analize, pogotovu besplatno na ES.
Najzad da se oko nečega složimo. Ja zaista sam umem najbolje da govorim o svojim namerama. Takođe, stojim iza onoga što sam napisao. Zar zaista misliš da iko može da ti napiše udžbenik analize besplatno i da ti ga tek tako okači na internet? Možda i može ako je penzioner, ali uranium je tek student.
Uranium me je vrlo dobro razumeo. Cela ova rasprava je besciljna. On samo troši svoje dragoceno vreme pokušavajući da ti objasni realne brojeve, ali od tog posla (bar na ovaj način) nema ništa. Ti nećeš biti na dobitku, a on će biti na gubitku. Da bi ti razumeo zasnivanje realnih brojeva i matematičke analize (uključujući pojmove kao što su dužina, površina, zapremina i mera ugla), ne možeš proći "jeftinije" od 150 stranica teksta minimum, ako ne i više. Tako bi ti eventualno razumeo pomenutu tematiku. Zar zaista očekuješ od nekoga ko je student da ti napiše knjižurinu za dž i tek tako je okači na internet?
Ne kažem, postoje free softverski proizvodi koji su kvalitetni, pa i tekstovi koji su u sličnom duhu. No, u svakom slučaju, tako se nešto radi za malo širu publiku i postoje načini da se takvi projekti održe. Profesor Matematičkog fakulteta Dr Miodrag Mateljević je napisao za studente besplatne knjige u elektronskom obliku i okačio ih na internet. Svaka mu čast! No, on prima platu na fakultetu, pa mu se može. Ako neko nema druge izvore prihoda, onda mora nekako da reši problem finansiranja tog projekta. Postoje razni načini, ali nikako putem pisanja za jednu osobu za dž. Ne razumem šta tu nije jasno. [ galet@world @ 25.10.2006. 20:56 ] @
Citat: Nedeljko: Ne razumem šta tu nije jasno.
Dugo sam razmišljao da li da ti pomognem da razumeš ili ne.
Nisam izdržao da te držim u neizvesnosti i zato ovo moram da ti kažem:
Evo šta ti ne razumeš: Ako deliš jabuku na beskonačno mnogo delova - jedan takav deo je, ma koliki bio, deo jabuke!
Verujem da (ipak) razumeš šta sam ovim hteo da kažem.
Ja nisam hteo da se "ogrebem" za besplatan i problematičan udžbenik (koji je već mnogo puta napisan!), nego sam hteo da tebe besplatno nečemu naučim.
Ako ti neko uzme jabuku onda nemaš ništa od jabuke, jednako tako kao ni od onoga što nikad nisi ni imao.
[ Nedeljko @ 27.10.2006. 09:19 ] @
Ama, kažem ja da ćemo uživati u tvojim časovima. Samo tako nastavi. No, ipak, da bi neko nešto preneo, prvo mora sam to da poseduje.
Citat: galet@world: Ja nisam hteo da se "ogrebem" za besplatan i problematičan udžbenik (koji je već mnogo puta napisan!),
Da si ikada pročitao barem jedan u kome se zasnivaju realni brojevi, ne bi postavljao pitanja kao što je ono iz prvog posta ove teme. Uranijum ti je dobro odgovorio pitanjem - "A šta podrazumevaš pod količinom?", no ti ne možeš da shvatiš smislenost takvog odgovora.
Što se jabuke tiče, možemo umesto o njoj (koja nije matematički pojam) govoriti o skupovima tačaka (što jeste matematički pojam). Oni nisu isto što i realni brojevi, ali postoji veza izmežu skupova tačaka u prostoru i realnih brojeva. Ta veza se zove Lebegova mera koja (nekim, ne baš svim) skupovima tačaka u prostoru pridružuje realan broj ili beskonačnost (kao jedinstvenu konstantu). Prazan skup, tačka, prava i ravan svakako da nisu isto, ali u prostoru imaju istu Lebegovu meru - a to je 0. To je kao što crvena ruža i crveni karanfil nisu isto, ali imaju istu boju. [ galet@world @ 27.10.2006. 20:56 ] @
Nedeljko
Drago mi je što te uveseljavam, kad već ne mogu da te naučim.
Ali da pokušam još jednom, pa ako ne uspem bar ću te nasmejati.
Ako imaš kilogram pšenice, onda tu pšenicu možeš da melješ iliti usitnjavaš koliko god hoćeš. Uvek od sitnog može biti sitnije.
Ali uvek ćeš imati kilogram brašna sve sitnijeg i finijeg.
“Brašno je neuništivo!!!”
(Nemoj misliti na atomske ili subatomske čestice, to je zamorno, nego zamisli da je brašno elementarna materija – tako će ti biti lakše)
I sad ako si podelio 1 kg pšenice na beskonačno mnogo delova dobio si onu tvoju nulu bez dimenzije, a kad bi pšenica bila moja - ja bi dobio nulu sa dimenzijom pšeničnog brašna.
Ti ne možeš da umesiš hleb od beskonačno mnogo tvojih nula, ja od mojih mogu.
Ja verovatno po tvom mišljenju opet grešim, pa verujem da ćeš se i na ovo moje brašno nasmejati!
Ali, nema veze, budi ti zdrav i veseo!
[ Nedeljko @ 28.10.2006. 08:20 ] @
Ajmo ovako, Imam 1kg gline. Podelim je na 1000 jednakih delova. Oni su mase po 1g. Dakle, svaki od njih ima pozitivnu masu. Te delove podelimo na po 1000 jednakih delova. Sada imamo 10 6 delova (još uvek konačno mnogo) od kojih je svaki mase po 1mg. Podelimo svaki od njih na po 1000 jednakih delova. Sada imamo 10 9 delova (ali ipak konačno mnogo) od kojih je svaki mase 1 mikrogram. Podelimo li i njih na po 1000 jednakih delova, imaćemo 10 12 delova (što je još uvek konačno mnogo) mase od po 1ng. I tako dalje, koliko god delili, uvek ćemo imati konačno mnogo delova. Podeli koliko god hoćeš konačno mnogo delova na po konačno mnogo delova, opet ćeš imati konačno mnogo.
E sad, Lebegova mera (na pravoj) skupa racionalnih brojeva (koji se sastoji od beskonačno mnogo tačaka) je 0, baš kao i od konačnih skupova tačaka uključujući i prazan skup. Lebegova mera (na pravoj) odsečka [0,1], (koji se takođe sastoji od beskonačno mnogo tačaka) je 1. Čak i u računu graničnih vrednosti (koji nema baš puno veze sa ovim) 0 puta beskonačno nije uvek nula, već u principu neodređen izraz. To znači da ako o jednom nizu znamo da teži nuli, a o drugom da teži beskonačnosti, to je i dalje nedovoljna količina informacija da bismo zaključili nešto o konvergenciji proizvoda tih nizova. Gde li si samo iskopao obrazac 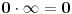 na koji se stalno pozivaš?
Da li znaš da je po teoremi Banaha i Tarskog moguće podeliti loptu na konačan broj delova (ne više od 11, a Robinson je broj delova smanjio na 5), tako da se od tih delova (samo kretanjem, bez ikakvih deformacija) mogu dobiti dve takve kugle? Jedna od posledica je da slona od deset tona možeš da podeliš na konačan broj delova i da ih nepromenjene sve smestiš u trbuh malog miša bez da se guraju.
http://mathworld.wolfram.com/Banach-TarskiParadox.html
http://en.wikipedia.org/wiki/Banach%E2%80%93Tarski_paradox
http://www.kuro5hin.org/story/2003/5/23/134430/275
http://www.math.hmc.edu/funfacts/ffiles/30001.1-3-8.shtml
Malo ozbiljniji tekst je
http://www.math.hmc.edu/~su/papers.dir/banachtarski.pdf
[Ovu poruku je menjao Nedeljko dana 28.10.2006. u 12:03 GMT+1][ galet@world @ 28.10.2006. 18:18 ] @
Ajmo i ovako:
Ako duzinu od 1 m podelis na 100 delova, pa opet svaki taj deo na 100 delova i t. d. svaki taj deo ima duzinu i dve krajnje tacke.
Pitanje je: kada taj deo prestaje da ima duzinu, odnosno kada prestaja da ima dve krajnje tacke?
[ Nedeljko @ 28.10.2006. 19:04 ] @
Odgovor: Ne prestaje nikad.
[ galet@world @ 29.10.2006. 15:15 ] @
Sad mi zaista vise nisi jasan - odgovorio si u skladu sa mojim misljenjem!
[ Nedeljko @ 29.10.2006. 23:03 ] @
Super. Znači, nema beskonačno kratkih duži koje se ne svode na tačku.
[ galet@world @ 30.10.2006. 07:00 ] @
Upotrebio si dve negacije, da ne bi doslo do zabune pitam - da li to znaci ca se svaka besonacno mala duzina svodi na tacku?
[ chupcko @ 30.10.2006. 10:17 ] @
Jel se secate onog dokaza da je krodil duzi nego sto je siri ?
Lema 1: Krokodil je zeleniji nego sto je siri.
Dokaz:
Krokodil je zelen i po duzini i po sirini dok je sirok samo po sirini, pa je zato krokodil zeleniji nego sto je siri.
Kraj dokaza.
Lema 2: Krokodil je duzi nego sto je zeleniji.
Dokaz:
Krokodil je dugacak i sa gornje i donje strane, ali je zato zelen samo sa gornje, pa je zato krokodil duzi nego sto je zeleniji.
Kraj dokaza.
Dokaz sledi iz Leme 1 i Leme 2.
A sada malo ozbiljnosti: ajde bre kupi lepo analizu 1 i 2 od Adnadjevica i Kadelburga, ili neku drugi ekvivaletnu knjigu paaaaaaa ce sve biti jasnije :).
P.S. Tacka je ono ciji je deo nista :)))), prava je duzina bez sirine :)))))))
[ Nedeljko @ 30.10.2006. 12:31 ] @
@galetworld
Da, to znači to. Pod beskonačno kratkom duži tu podrazumevam duž koja je kraća od 1/n za svaki prirodan broj n. U standardnom zasnivanju polja realnih brojeva nema takvih pozitivnih veličina, pa je jedina preostala mogućnost 0. Tada se duž (ukoliko je zatvorena) svodi na tačku.
Citat: chupcko: Jel se secate onog dokaza da je krodil duzi nego sto je siri ?
Krokodil svakako jeste više dugačak nego širok. Verovatno si mislio na dokaz da je obrnuto: širi je nego zeleniji zato što je zelen samo sa gornje, a širok i sa gornje i sa donje strane, a zeleniji je nego duži zato što je zelen i po širini i po dužini, a dugačak samo po dužini.
Citat: chupcko: A sada malo ozbiljnosti: ajde bre kupi lepo analizu 1 i 2 od Adnadjevica i Kadelburga, ili neku drugi ekvivaletnu knjigu paaaaaaa ce sve biti jasnije :).
Ne vredi, džaba pričaš. Ja sam već omutaveo. On želi da samostalno ispituje koncept realnih brojeva, pri čemu ga ne zanimaju postojeći koncepti, već se oslanja na sopstvenu intuiciju o tome. Neka me ispravi ako grešim. No, pametnije je naučiti postojeće koncepte, pa im onda nalaziti nedostatke i razvijati nove koncepte koji ih otklanjaju. [ galet@world @ 30.10.2006. 17:48 ] @
Citat: Nedeljko: Pod beskonačno kratkom duži tu podrazumevam duž koja je kraća od 1/n za svaki prirodan broj n. U standardnom zasnivanju polja realnih brojeva nema takvih pozitivnih veličina, pa je jedina preostala mogućnost 0. Tada se duž (ukoliko je zatvorena) svodi na tačku.
Ta jedina preostala vrednost znači nepostojanje i prelaskom na tu vrednost učinio si kvalitativni skok koji ne pripada postupku deljenja, prešao si na nešto novo, drugo, nepostojeće koje nema nikakve veze sa onim što si započeo.
Rekao si da postupkom deljenja svaki deo ima dužinu i dve krajnje tačke i rekao si da taj deo ne prestaje nikad da ima dužinu i dve tačke ma koliko mali bio - i to je u redu, a sad kažeš da ipak prestaje i da se svodi na nulu.
Zašto? Zato što nam "preostaje" samo nula? Nula nije nikakva preostala mogućnost. Ona s tim ima veze isto toliko koliko i zeleni krokodil.
Nula o kojoj ti govoriš nikakve veze nema sa usitnjavanjem koje smo započeli. To je nešto drugo. Nešto što nije nastalo deljenjem dužine. Nešto što utrpavaš tamo gde ne pripada.
Duž se svodi na tačku!!! Fenomenalno.
Duž dakle nestaje. Uništena je. U jednom nedozvoljenom i besmislenom skoku! Alal vera matematičari.
Chupcko - ako me upućuješ na neke knjige onda me upućuješ i na autore tih knjiga - zato što ti lično ne ćeš da budeš autor razumnog odgovora. Šta su ti autori bolji od tebe, ako znaš odgovore.
[ Nedeljko @ 30.10.2006. 20:04 ] @
Citat: galet@world: Rekao si da postupkom deljenja svaki deo ima dužinu i dve krajnje tačke i rekao si da taj deo ne prestaje nikad da ima dužinu i dve tačke ma koliko mali bio - i to je u redu, a sad kažeš da ipak prestaje i da se svodi na nulu.
Nigde nisam rekao da u pomenutom postupku duži prestaju da imaju dužinu veću od nule. Napisao sam sledeće
Citat: Nedeljko: Odgovor: Ne prestaje nikad. Citat: Nedeljko: Super. Znači, nema beskonačno kratkih duži koje se ne svode na tačku. Citat: Nedeljko: Da, to znači to. Pod beskonačno kratkom duži tu podrazumevam duž koja je kraća od 1/n za svaki prirodan broj n. U standardnom zasnivanju polja realnih brojeva nema takvih pozitivnih veličina, pa je jedina preostala mogućnost 0. Tada se duž (ukoliko je zatvorena) svodi na tačku.
Znači, to je bio opis pojma "beskonačno kratke duži" za koju sam tvrdio da je u postupku delenja nikada ne dobijamo.
Citat: galet@world: Duž se svodi na tačku!!! Fenomenalno.
Vidiš, za razliku od tebe, ja vodim računa o tome da svi pojmovi budu precizno definisani, pa tako i ovde navodim definiciju duži koju koristim.
Za ma koje tačke A i B pod (zatvorenom) duži AB podrazumevam skup svih tačaka na pravoj AB koje su između tačaka A i B (ako ih ima) i još tačke A i B. U posebnom sličaju, ako je A=B, onda se duž AB svodi na jednu tačku.
Dakle, ja koristim tu definiciju. Možemo koristiti i neku drugu. To je stvar dogovora. Tu niko ne može biti "u pravu", niti "u krivu". [ galet@world @ 31.10.2006. 07:28 ] @
Citat: Nedeljko: Znači, to je bio opis pojma "beskonačno kratke duži" za koju sam tvrdio da je u postupku delenja nikada ne dobijamo.
Duž koju ne dobijamo postupkom deljenja nije više duž.
"Duž" koja nema dva kraja nije više duž.
Beskonačno kratka duž je razmak između dve susedne tačke.
"Duž" koja se svodi na jednu tačku nije više duž - to je skok na drugu pojavu
Četvorougao kojemu nestane jedna strana nije više četvorougao nego trugao.
Ako vrh nekog trougla nije jedna tačka neko dve susedne onda je to još uvek četvorougao kojemu četvrtu stranu predstavlja beskonačno kratka duž.
Ako nestane ta beskonačno kratka duž t. j. ako u vrhu četvorougla ne postoje dve tačke nego jedna - onda je to skok na drugu pojavu - trougao.
Takva nula o kojoj ti govoriš znači nepostojanje, nemanje, isključenje, preskok na nešto drugo zbog nestanka nekog bitnog definišućeg elementa.
[ Nedeljko @ 31.10.2006. 08:29 ] @
Citat: galet@world: Duž koju ne dobijamo postupkom deljenja nije više duž.
Bravo! Znači, ako na realnoj pravoj deliš duž [0,1], onda [2,3] nije duž zato što nije dobijena postupkom delenja.
Citat: galet@world: Beskonačno kratka duž je razmak između dve susedne tačke.
Ovo mi se još više sviđa. Znači, ako su A i B različite tačke realne prave (recimo da je Alevo od B), onda tačka (A+B)/2 može da ne pripada duži AB. Ako su P i Q "susedne tačke", šta je onda središte takve duži?
Citat: galet@world: "Duž" koja se svodi na jednu tačku nije više duž - to je skok na drugu pojavu
Mogu da prihvatim takvu definiciju duži za nastavak razgovora. No, ona se ne može odnositi na moj post u kome sam koristio drugačiju terminologiju. Oko jezika se možemo dogoovriti. Sadržaj je bitan. [ galet@world @ 31.10.2006. 20:42 ] @
Citat: Nedeljko: Znači, ako na realnoj pravoj deliš duž [0,1], onda [2,3] nije duž zato što nije dobijena postupkom delenja
Greška! Ne znači. Duž [2,3] je deo te prave.
Najpre si realnu pravu podelio na dva dela, pa si jedan deo podelio na dva nejednaka dela a duž [2,3] je manji deo.
Citat: Nedeljko: Ovo mi se još više sviđa.
Suvišno. Ne verujem da nekoga interesuju tvoja osećanja.
Citat: Nedeljko: Ako su P i Q "susedne tačke", šta je onda središte takve duži?
P + 0[m]/2 ili Q – 0[m]/2
Ovo u zagradama potiče od dimenzije duži (na primer u metrima [m]), a ne od dimenzije sile ili stepeni i t. d.
Ovo je nula koja pamti svoje poreklo, ali ne samo po vrsti dimenzije nego i nastanku.
Citat: Nedeljko: Mogu da prihvatim takvu definiciju duži za nastavak razgovora
Kako to misliš da se definicija duži može prihvatiti uz uslov koji nema veze sa tom definicijom?
[ Nedeljko @ 01.11.2006. 07:54 ] @
O ostalim tvojim greškama ću kasnije. Za sada mi reci jesu li te tačke između tačaka P i Q ili ne. [ galet@world @ 01.11.2006. 13:21 ] @
To je jedna tačka u središtu te duži.
[ Nedeljko @ 01.11.2006. 15:35 ] @
A da li je ona između tačaka P i Q? Ako jeste, kako tačke P i Q mogu biti susedne, ako ima tačaka između njih?
[ galet@world @ 01.11.2006. 18:01 ] @
Ja sam rekao da "tvoja" nula znači nepostojanje i dobija se oduzimanjem dve jednake veličine.
"Moja" nula ne znači nepostojanje nego je rezultat deobe, na primer duži, na beskonačno mnogo delova
Duž je konačan kontinuitet koji ima krajeve
Šta znači kraj duži? To je prestanak kontinuiteta. To je mesto gde više nema te pojave. To je ona "tvoja" nula koja znači nepostojanje. To mesto možeš nazvati tačkom.
Beskonačno kratka duž ima takva dva mesta t.j. dva kraja, a između njih je kontinuitet koji ima dužinu nula, ali ne "tvoja" nula koja znači nepostojanje, nego "moja" nula koja je dobijena beskonačnom deobom kontinuiteta i koja egzistira i zadržala je dimenziju kao kvalitet (iliti "miris" t. j. "miriše na dužinu") koji tom deobom ne može biti uništen.
E sad:
Citat: A da li je ona između tačaka P i Q? Ako jeste, kako tačke P i Q mogu biti susedne, ako ima tačaka između njih?
Ako između tačaka P i Q "uglaviš" tačku koja nema dimenziju to ti je isto kao da ništa nisi ni uradio. Time nisi ukinuo susedstvo tačaka P i Q kao krajeva kontinuiteta. Tih uglavljenih tačaka tu može stati koliko god hoćeš jer njima ne treba neki "prostor" da bi se "smestile" jer nemaju dimenziju.
Dakle tačke P i Q ostaju susedne jer ustvari nisi između njih stavio ništa. [ LightBow @ 07.11.2006. 00:54 ] @
Citat: chupcko:: Jel se secate onog dokaza da je krodil duzi nego sto je siri ?
[ Nedeljko @ 08.01.2009. 18:44 ] @
Ovde nije jasno šta galet@world zapravo hoće.
1. Ako hoće da kritikuje neko od postojećih zasnivanja analize, onda bi trebao prvo da ga nauči.
2. Ako hoće da uvede neko novo zasnivanje analize, onda bi trebao da strogo izloži taj sistem (bilo aksiomatski, bilo modelski).
Kada se ne zna šta se hoće, onda je sve uzalud.
[ senad_k @ 25.01.2009. 23:57 ] @
Pod cos 0 se podrazumijeva cos (0 rad) - oznaka za radijan se po konvenciji ne mora pisati ( po definiciji radijan se dobije dijeljenjem veličina istih dimenzija pa je bezdimenzionalan)
Dakle, cos 0 = 1 (isto kao i cos 0°)
[ Cabo @ 26.01.2009. 11:17 ] @
Citat: Mikky:
Slazem se sa uraniumom...
Realni brojevi su unija racionalnih i iracionlnih brojeva... e sad diskusiju mozete da prenesete na ova druga 2 skupa, pre svega na iracionalne :)
Kako definišeš iracionalne brojeve? Preko realnih? A kako onda definišeš realne? Preko iracionalnih... itd. u beskrajon. Circulus vitiosus.
@galet* (ako još prati):
Znaš li da postoje i beskonačni skupovi mere nula? Tačke nemaju dužinu. Jeste malo nezgodno za kapiranje, ali je tako. Kada shvatiš (ali stvarno) pojam konvergencije, sve će ti biti jasnije. Na primer, to zašto se izostavlja sama tačka kojoj konvergira argument kada se posmatra konvergencija funkcije u toj tački. Ili, kako to da 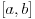 nije nije isto što i 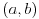 .
[Ovu poruku je menjao Cabo dana 26.01.2009. u 12:29 GMT+1]
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|