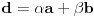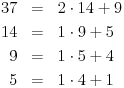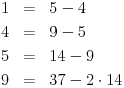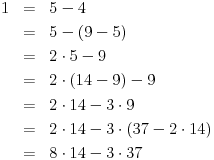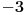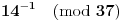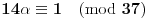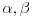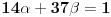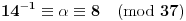trebam pojašnjenje zadatka

[ Davor Grubelić @ 21.09.2006. 17:03 ] @

pozdrav, genijalci.
trebam malu pomoć. zadatak je iz diskretne matematike (cikličke grupe).

trebam pojašnjenje ovog zadatka:

Code:

PRIMJER 3. U dokazu prethodnog teorema je zapravo opistana i konstrukcija inverznog elementa a-1 = k'.

Provedimo to na primjeru grupe Z*37 = {1, 2, ..... 36}. Broj p = 37 je prost. Nađimo 14-1 u toj grupi.
Da bismo došli do prikaza ka + lp = 1, gdje je a = 14, provedimo Euklidov algoritam:

(1)  p = 2a + 9 (nakon dijeljenja p sa a);
(2)  a = 1 · 9 + 5 (nakon dijeljenja a = 14 sa 9);
(3)  9 = 1 · 5 + 4 (nakon dijeljenja 9 sa 5);
(4)  5 = 1 · 4 + 1 (nakom dijeljenja 5 sa 4).

Iz (1) je 9 = p – 2a, pa uvrštavanjem u (2) dobivamo a = ( p- 2a ) + 5.
Zatim odavde izračunamo oststak 5 i uvrstimo u (3), te na kraju iz (3) izračunamo ostatak 4 i uvrstimo u (4).
Dobiva se 8a -3p = 1. Dakle 8a = 1 u grupi Z37, tj. a-1 = 14-1 = 8.

dali mi netko može pomoći? ako da, bio bi mu/joj jako zahvalan...

e da, ne kužim tu ništa....pa neka se nitko ne ljuti.

[ uranium @ 21.09.2006. 19:29 ] @

Euklidov algoritam se koristi za pronalaženje najvećeg zajedničkog delioca dva data cela broja.
U našem slučaju, kako su 37 i 14 uzajamno prosti, očekujemo da će Euklidov alg. dati broj 1 kao rezultat.
Uz to važi i sledeća teorema:

Ako je

najveći zajednički delilac brojeva

, onda važi

za neke

.

Vraćajući se unazad kroz pomenuti algoritam uvek možemo efektivno pronaći te brojeve

.

Dakle:

j-ne sada možemo da posmatramo u obrnutom poretku i ovako:

Krenućemo od prve jednačine i dokle god imamo odgovarajuću zamenu - brojeve na desnoj strani ćemo zamenjivati, izraz sređivati, pa opet zamenjivati...