_________________________
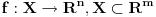
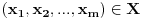
Kazemo da je funkcija diferencijabilna u tocki (oznacit cu je krace s a ne s M ), ako postoje:
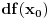
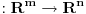
a) linearni operator "" i
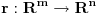
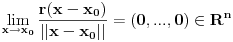
b) neka funkcija , sa svojstvom: (oznacimo je krace samo s 0),

takvi da vrijedi:

________________________

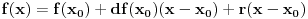
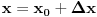
Kako je po pretpostavci f diferencijabilna u x_0, to za neki , vrijedi:
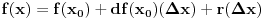
(*) i
(***).

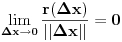
(*****)Treba pokazati da je f neprekidna u , tj treba pokazati da su sve tri funkcije s desne strane gornje jednakosti neprekidne u . Pa jer je zbroj neprekidnih funkcija, neprekidna funkcija, zakljucit cemo da je onda i f, kao njihov zbroj, neprekidna u :

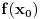
1) Najprije imamo konstantnu funkciju . Ona je neprekidna u jer su konstante neprekidne funkcije.

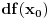
2) linearni operatori su neprekidne funkcije (dokazuje se tako sto se pokaze da svaki linearni operator ima Lipshitzovo svojstvo, pogledaj negdje medju teoremima), pa je i linearni operator neprekidan.

3)Da bismo pokazali da je r neprekidna u , pozvat cemo se na karakterizaciju neprekidnosti pomocu limesa, tj:

(****) r je neprekidna u akko je .

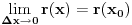Pokazimo to:

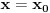
Najprije, uvrstimo li u (*) , imat cemo:
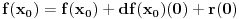
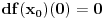
. Iz ovog, i zbog poznate cinjenice da svaki linearni operator nulu preslikava u nulu tj , slijedi da je

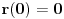
(**) (ne zaboravimo da je ova nula zapravo )

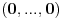
Sada zbog (***), prema definiciji granicne vrijednosti, vrijedi:
.
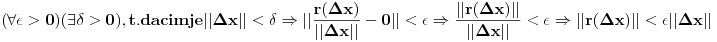
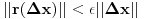
No , na osnovu gornjeg mozemo interpretirati ovako:


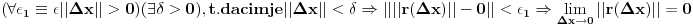
Kako je norma neprekidna, to limes i norma mogu komutirati pa zadnje mozemo pisati kao:
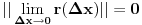
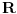
(ova nula je obicna nula iz skupa , jer je to vrijednost norme )

iz cega slijedi da je

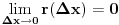
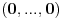
, (ova nula je pak ) sto zbog (**) mozemo pisati kao:



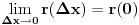
pa prema (****) zakljucujemo da je r neprekidna u .

I na kraju zbog recenoga u (*****) zakljucujemo da je f neprekidna u


Eto, a mozda moze i jednostavnije, ali jbga ja volim kad je sve jasno..

Hvala puno!