[ d3x @ 30.09.2006. 19:57 ] @
| Potrebno je naci svaki racionalan broj x za koji je i A(x) racionalan broj. Zatim treba izdvojiti sve prirodne za koje je izraz prirodan. |
|
[ d3x @ 30.09.2006. 19:57 ] @
[ milanche @ 30.09.2006. 20:46 ] @
Koren iz negativnog broja nije racionalan broj, sto diktira da izraz u zagradi mora da bude >= 0.
Posto je u pitanju kvadratni trinom ciji je vodeci koeficijent pozitivan, vrednost trinoma ce biti uvek pozitivna osim izmedju realnih nula. Tvoj zadatak je da pronadjes realne nule trinoma (tj. resi jednacinu 8x^2 -2x -3 = 0)i da iskljucis sve brojeve izmedju njih, ne ukljucujuci same realne nule. Preciznije receno, resenje je sledeci skup realnih brojeva: (-inf, x1] U [x2, +inf) Sto se tice drugog uslova - mrzi me da mislim kako da ga resim - cekaj nekog od mladjih i svezijih matematicarskih mozgova da uskoci i pomogne. [ d3x @ 01.10.2006. 01:56 ] @
hmm to je rjesenje koje daje REALAN broj zadatak se rijesi za 30sec, ali ovaj zadatak zahtjeva (sve) racionalne x koji daju racionalan A(x) :)
moj pokusaj je bio da izjednacim A(x) sa a/b ( b € N, a € N U {0} ) i onda izrazim x preko a i b. Dosao sam do: 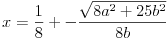 međutim ovo ne mogu ostaviti kao rjesenje, trebalo bi valjda x izraziti preko jedne promjenjive... ideje ? [ emiraga @ 01.10.2006. 06:53 ] @
ima li mozda mogucnosti da se smjenama svede na Pelovu_jednacinu ?
[ d3x @ 01.10.2006. 09:05 ] @
mozda i postoji, ali ja je ne vidim :)
[ uranium @ 01.10.2006. 16:49 ] @
Neka je
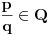 . Iz . Iz 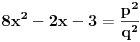 dobijamo dobijamo 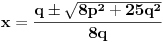 Sada nam ostaje da vidimo kada jednačina 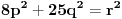 ima cela rešenja (dovoljno je da pronađemo ona kod kojih je ima cela rešenja (dovoljno je da pronađemo ona kod kojih je 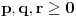 ) )odatle imamo: 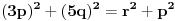 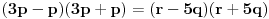 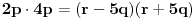 Neka je 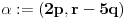 i i 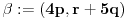 , otuda za neke cele , otuda za neke cele 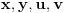 važi: važi: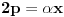 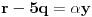 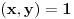 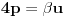 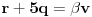 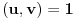 nakon odgovarajućih smena imamo: 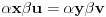 tj. tj. 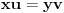 . .Pošto je 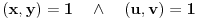 i i 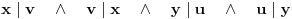 dobijamo dva slučaja: dobijamo dva slučaja: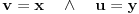 ili ili 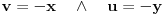 . .1. slučaj: 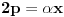 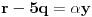 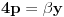 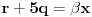 otuda 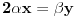 uzmimo da je 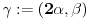 , onda je za neke cele , onda je za neke cele 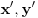 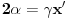 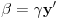 pa dobijamo: 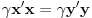 a otuda zbog a otuda zbog 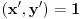 sledi i sledi i i) 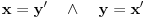 ii) 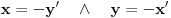 Naravno, dovoljno je da proučimo samo prvi slučaj. Dakle, imamo 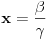 i i 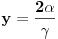 a otuda i: a otuda i: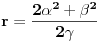 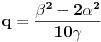 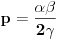 Proverimo da mora biti 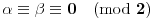 : :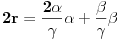 Leva strana je parna, pogledajmo šta se dešava sa parnošću desne u nekoliko slučajeva: 1. Ako je 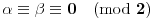 , desna strana (po modulu 2) je , desna strana (po modulu 2) je 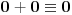 . .2. Ako je 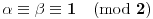 , onda je , onda je 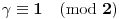 pa je desna strana (po modulu 2) pa je desna strana (po modulu 2) 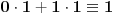 3. Ako je 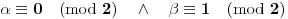 , onda je , onda je 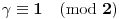 pa je desna strana (po modulu 2) pa je desna strana (po modulu 2) 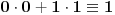 4. Ako je 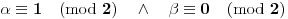 , onda je , onda je 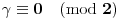 pa je desna strana (po modulu 2) pa je desna strana (po modulu 2) 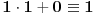 Proverimo da mora biti i 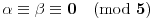 da bi da bi 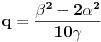 bilo celo. bilo celo.To možemo videti na sledeći način: kvadratni ostaci po modulu  su su 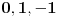 , pa ako bi trebalo da važi , pa ako bi trebalo da važi 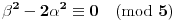 tj. tj. 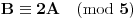 gde su gde su  i i  kvadratni ostaci po modulu kvadratni ostaci po modulu  - lakom proverom zaključujemo da je jedina mogućnost - lakom proverom zaključujemo da je jedina mogućnost 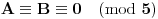 tj. tj. 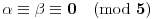 . .Da zaključimo, ako je 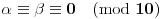 i i 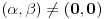 , onda su rešenja: , onda su rešenja: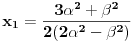 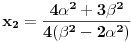 Jasno je da je uvek 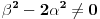 , (osim u trivijalnom slučaju koji smo već isključili) , (osim u trivijalnom slučaju koji smo već isključili) 2. slučaj: se radi analogno, a rešenja dobijena u tom slučaju već su obuhvaćena rešenjima prvog slučaja. Ostaje još da se vidi kada je 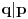 i i 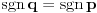 i i 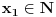 ili ili 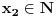 ... ...ako baš niko ne bude hteo, onda ću ja malo kasnije [Ovu poruku je menjao uranium dana 01.10.2006. u 20:37 GMT+1] [ emiraga @ 30.03.2008. 12:22 ] @
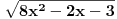 ce biti prirodan ako je ce biti prirodan ako je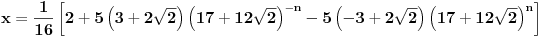 za cjelo za cjelo  . .Rjesenje se dobiva slicno kao za Fibonacijeve brojeve. Svi  za koje je onaj korijen prirodan broj je niz od za koje je onaj korijen prirodan broj je niz od  : {2,62,2102,71402,2425562,...} : {2,62,2102,71402,2425562,...}Primjetiti da se dijeljenjem dva susjedna broja u nizu od  , konvergira prema dva broja koja su rjesenja jednacine , konvergira prema dva broja koja su rjesenja jednacine 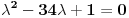 . .Tada se uspostavi rekurentna relacija 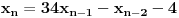 . (uz . (uz 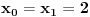 ) )I onda se to pretvori u matricnu formu  Odakle se primjenom Jordanove formule za stepenovanje ( 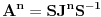 ) dobija rezultat. ) dobija rezultat.[Ovu poruku je menjao emiraga dana 30.03.2008. u 13:39 GMT+1] Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|