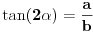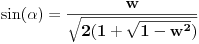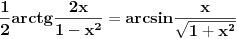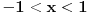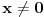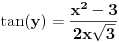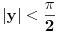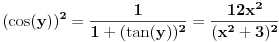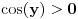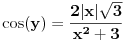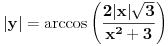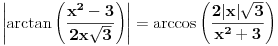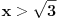[ shiggy @ 06.10.2006. 22:14 ] @
|
[ uranium @ 07.10.2006. 13:41 ] @
[ Farenhajt @ 07.10.2006. 20:42 ] @
[ uranium @ 07.10.2006. 20:49 ] @
[ Farenhajt @ 07.10.2006. 23:44 ] @
Aha, tačno. Pardon
[ shiggy @ 08.10.2006. 01:08 ] @
hvala svima
[ devetkamp @ 25.12.2011. 12:13 ] @
[ SrdjanR271 @ 25.12.2011. 21:00 ] @
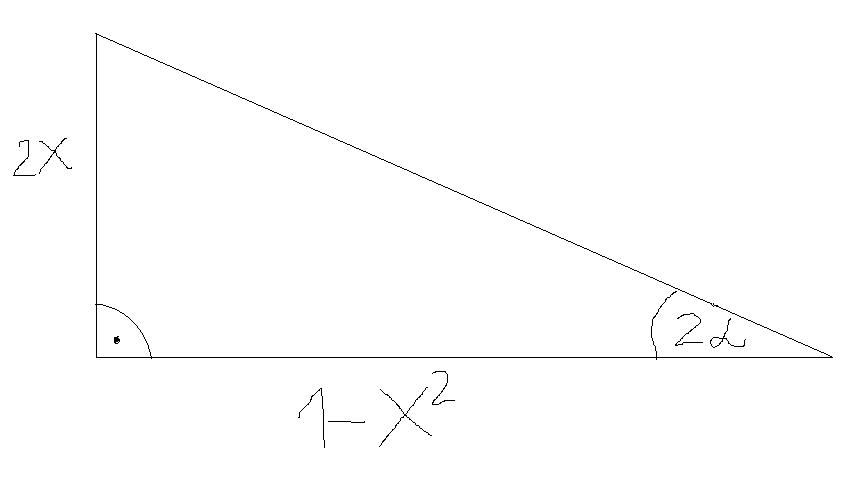 Nađeš tangens od 2 alfa, i sinus alfa, preko x. Posle izraziš alfa preko arctg i arcsin. [ devetkamp @ 26.12.2011. 13:01 ] @
Hvala puno, nista bez vas.... :D
[ devetkamp @ 27.12.2011. 19:35 ] @
Uf. Ja bas zakasao sa ovim arkus funkcijama. Problem je sledeci: Data je funkcija
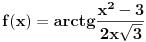 . Datu funkciju sam izrazio preko . Datu funkciju sam izrazio preko 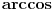 funkcije, i dobio da je data funkcija jednaka sa funkcije, i dobio da je data funkcija jednaka sa 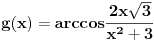 . Medjutim, te funkcije nisu jednake za svako x. Pitanje je kako odrediti te uslove? Da li treba da koristim definisanost arkusa? . Medjutim, te funkcije nisu jednake za svako x. Pitanje je kako odrediti te uslove? Da li treba da koristim definisanost arkusa?  , , 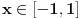 . Ili ima tu jos nesto? Moze li x da bude 0? Posto vazi . Ili ima tu jos nesto? Moze li x da bude 0? Posto vazi 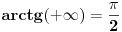 . Hvala... . Hvala...[ Nedeljko @ 27.12.2011. 21:49 ] @
[ devetkamp @ 28.12.2011. 12:47 ] @
[ Sini82 @ 28.12.2011. 15:41 ] @
Nedeljko je pokazao da jesu jednaki, ostaje još da pokažemo za koje x-ove su jednaki.
Imamo 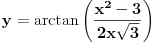 i i 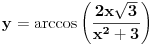 . .Pogledajmo grafike funkcija arctan i arccos: http://mathworld.wolfram.com/InverseTangent.html http://mathworld.wolfram.com/InverseCosine.html. Dobijamo: 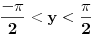 i i 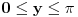 tj. (odredimo njihov presjek) tj. (odredimo njihov presjek) 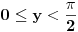 . .Odatle dalje dobijamo: 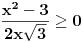 i i 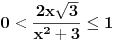 . .Rješavajući sistem nejednačina, dobijamo: 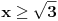 . .Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|